Denkbeeldige nummers eigenschappen, toepassingen, voorbeelden

De Denkbeeldige getallen Zij zijn degenen die oplossing geven aan de vergelijking waarin het onbekende, vierkant verhoogd, gelijk is aan een echt negatief getal. De denkbeeldige eenheid is I = √ (-1).

In de vergelijking: Z²= - a, Z Het is een denkbeeldig getal dat als volgt wordt uitgedrukt:

 Z = √ (-a) = i√ (a)

Wezen naar Een positief reëel getal. Ja A = 1, Dus z = i, waar Je is de denkbeeldige eenheid.

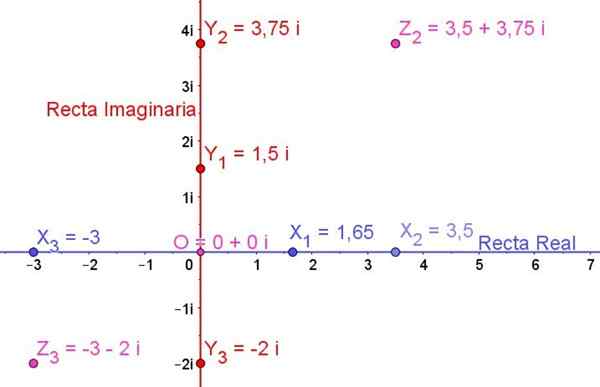Figuur 1. Complex vlak met enkele reële getallen, enkele denkbeeldige getallen en enkele complexe getallen. Bron: f. Zapata.

Over het algemeen wordt een denkbeeldig getal z altijd uitgedrukt in vorm: 

z = y⋅i

Waar En Het is een echt getal en Je is de denkbeeldige eenheid.

Evenals reële getallen worden op een lijn weergegeven, de naam van de Echt recht, Analoog de denkbeeldige getallen worden weergegeven op de Denkbeeldig recht.

De Denkbeeldig recht Het is altijd orthogonaal (90º vorm) naar de Echt recht en de twee lijnen definiëren een cartesiaans vlak genaamd de Complex vlak.

Figuur 1 toont het complexe vlak en enkele reële getallen, enkele denkbeeldige getallen en ook enkele complexe getallen worden erop weergegeven:

X₁, X₂, X₃ Het zijn echte cijfers

EN₁, EN₂, EN₃ Het zijn denkbeeldige cijfers

Z₂ en z₃ Het zijn complexe cijfers

Het nummer of is de echte nul en is ook de denkbeeldige nul, zodat de oorsprong of het nulcomplex wordt uitgedrukt door:

0 + 0i 

[TOC]

Eigenschappen

De set denkbeeldige getallen wordt aangegeven door:

I = ..., -3i, ..., -2i, .. .,-Yo, .. .,0i, .. .,Yo, .. .,2i, .. .,3i,…

En sommige bewerkingen over deze numerieke set kunnen worden gedefinieerd. Een denkbeeldig nummer wordt niet altijd verkregen uit deze bewerkingen, dus we zullen ze met een beetje meer detail zien:

Som en aftrekking van denkbeeldig

Denkbeeldige getallen kunnen van elkaar toevoegen en aftrekken en als gevolg daarvan zal er een nieuw denkbeeldig nummer zijn. Bijvoorbeeld:

Kan u van dienst zijn: Relatieve neven: wat zijn, uitleg, voorbeelden

 3i + 2i = 5i

4i - 7i = -3i

Denkbeeldig product

Wanneer het product van een denkbeeldig nummer met een ander wordt gemaakt, is het resultaat een reëel getal. Laten we de volgende bewerking doen om te controleren:

2i x 3i = 6 x i² = 6 x (√ (-1))² = 6 x (-1) = -6.

En zoals we zien, is de -6 een reëel getal, hoewel deze is verkregen door twee pure denkbeeldige getallen te vermenigvuldigen.

Product van een reëel getal voor een ander denkbeeldig

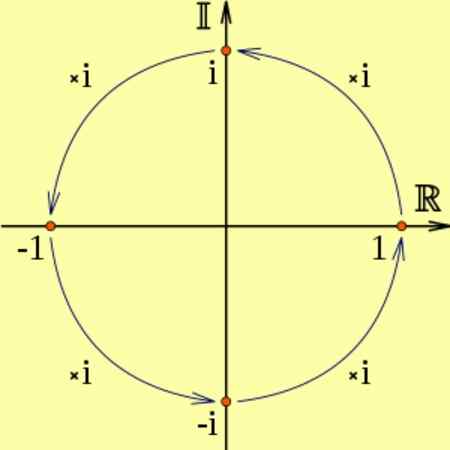
Als een reëel getal wordt vermenigvuldigd met I, is het resultaat een denkbeeldig getal, dat overeenkomt met een rotatie van 90 graden.

En is dat ik² komt overeen met twee opeenvolgende rotaties van 90 graden, wat gelijk is aan het vermenigvuldigen met -1, dat wil zeggen i² = -1. Het is te zien in het volgende diagram:

Figuur 2. De vermenigvuldiging door de denkbeeldige eenheid en komt overeen met 90º rotaties. Bron: Wikimedia Commons.

Bijvoorbeeld:

-3 x 5i = -15i

-3 x i = -3i.

Versterking van een denkbeeldige

De versterking van een denkbeeldig getal voor een volledige exponent kan worden gedefinieerd:

Je¹ = I

Je² = i x i = √ (-1) x √ (-1) = -1

Je³ = I x i² = -I

Je⁴ = I² X I² = -1 x -1 = 1

Je⁵ = I x i⁴ = I

Over het algemeen moet je Je^N = i^(n mod 4), waar Modder Het is het residu van de verdeling tussen N En 4.

De versterking van negatieve gehele getallen kan ook worden gemaakt:

Je^-1 = 1 / i¹ = i / (i x i¹) = I / (i²) = I / (-1) = -i

Je-² = 1 / i² = 1/ (-1) = -1

Je-³= 1 / i³ = 1 / (-i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

Over het algemeen is het denkbeeldige getal B⋅i verheven tot kracht n:

(B⋅i) i^N = B^N Je^N = B^N i^(n mod 4)

Enkele voorbeelden zijn de volgende:

(5 i)¹² = 5¹² Je¹² = 5¹² Je⁰ = 5¹² x 1 = 244140625

(5 i)^elf = 5^elf Je^elf = 5^elf Je³ = 5^elf x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ Je¹⁰ = 2¹⁰ Je² = 1024 x (-1) = -1024

Som van een reëel getal en één denkbeeldig

Wanneer een reëel getal wordt toegevoegd met een denkbeeldige, is het resultaat noch echt noch denkbeeldig, het is een nieuw type nummer dat wordt genoemd Complex nummer.

Als bijvoorbeeld x = 3,5 en y = 3,75i, dan is het resultaat het complexe nummer:

Kan u van dienst zijn: minimale vierkanten

Z = x + y = 3,5 + 3,75 i

Merk op dat de echte en denkbeeldige onderdelen niet in de som kunnen worden gegroepeerd, dus een complex nummer zal altijd een echt deel hebben en een ander denkbeeldig onderdeel.

Deze bewerking breidt de reeks reële getallen uit tot de breedste complexe getallen.

Toepassingen

De naam van denkbeeldige getallen werd voorgesteld door de Franse wiskundige René Descartes (1596-1650) als een aanfluiting of onenigheid met het voorstel van hen gedaan door de Italiaanse wiskundige van de Raffaelle Century Bombelli.

Andere grote wiskundigen, zoals Euler en Leibniz, detacheerden Descartes in dit meningsverschil en noemden denkbeeldige getallen als amfibie -cijfers, waarover werd gedebatteerd tussen zijn en niets.

De naam van denkbeeldige getallen wordt tegenwoordig gehandhaafd, maar het bestaan ​​en het belang ervan zijn zeer reëel en voelbaar, omdat ze op veel fysica van natuurkunde van nature verschijnen, zoals:

-De relativiteitstheorie.

-In elektromagnetisme.

-Kwantummechanica.

Oefening met denkbeeldige getallen

- Oefening 1

Zoek de oplossingen van de volgende vergelijking:

Z² + 16 = 0

Oplossing

Z² = -16

Square wortel in beide leden die je hebt:

√ (z² ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Met andere woorden, de oplossingen van de oorspronkelijke vergelijking zijn:

z = +4i of z = -4i.

- Oefening 2

Zoek het resultaat van het verhogen van de denkbeeldige eenheid om 5 min minus aftrekking de denkbeeldige eenheid verhoogd tot stroom -5.

Oplossing

Je⁵ - Je-⁵ = I⁵ - 1/i⁵ = i - 1/i = i - (i)/(i x i) = i - i/( - 1) = i + i = 2i

- Oefening 3

Zoek het resultaat van de volgende bewerking:

(3i)³ + 9i 

Oplossing

3³ Je³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Oefening 4

Zoek de oplossingen van de volgende kwadratische vergelijking:

Kan u van dienst zijn: bestaan ​​en uniekheid Stelling: demonstratie, voorbeelden en oefeningen

(-2X)² + 2 = 0

Oplossing

De vergelijking wordt als volgt herschikt:

(-2X)² = -2

Neem dan een vierkantswortel in beide leden

√ ((-2x)²) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Dan wordt X eindelijk verkregen:

x = ± √2 / 2 i

Dat wil zeggen, er zijn twee mogelijke oplossingen:

x = (√2 / 2) i

Of deze andere:

x = - (√2 / 2) i

- Oefening 5

Zoek de waarde van z gedefinieerd door:

Z = √ (-9) √ (-4) + 7

Oplossing

We weten dat de vierkantswortel van een negatief reëel getal een denkbeeldig getal is, bijvoorbeeld √ (-9) is gelijk aan √ (9) x √ (-1) = 3i.

Aan de andere kant is √ (-4) gelijk aan √ (4) x √ (-1) = 2i.

Zodat de oorspronkelijke vergelijking kan worden vervangen door:

3i x 2i - 7 = 6 i² - 7 = 6 (-1) -7 = -6 -7 = -13

- Oefening 6

Zoek de waarde van z als gevolg van de volgende verdeling van twee complexe getallen:

Z = (9 - i²) / (3 + i)

Oplossing

De expressienummer kan rekening houden met de volgende eigenschap:

Een verschil van vierkanten is het product van de som door het verschil van de binomials zonder het vierkant op te voeden.

Dus:

Z = [(3 - i) (3 + i)] / (3 + i)

De resulterende uitdrukking wordt vervolgens vereenvoudigd door te blijven

Z = (3 - i)

Referenties

1. Earl, r. Complexe getallen. Hersteld van: wiskunde.os.AC.Uk.
2. Figuera, j. 20000000000000000000. Wiskunde 1e. Diversifieerd. Co-bo edities.
3. Hoffmann, J. 2005. Selectie van wiskundeproblemen. Monfort Publications.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Denkbeeldig nummer. Opgehaald uit: in.Wikipedia.borg