Dubbele bemonstering

We leggen uit wat dubbele bemonstering, voorbeelden, voor- en nadelen is en opgeloste oefeningen

In dubbele bemonstering wilt u een dieper weten een variabele van een populatie

Wat is dubbele bemonstering?

Hij Dubbele bemonstering Het is een techniek die wordt gebruikt in inferentiële statistieken wanneer u meer detail en zekerheid wilt weten over een bepaalde variabele, die een bepaalde populatie kenmerkt.

De tweede populatiemonster wordt in het algemeen uitgevoerd na een eerste steekproef, waarvan de analyse geen statistisch significante conclusie aantoonde over een van de studievariabelen was genomen en geanalyseerd.

Om deze reden staat steekproef van dubbele statistieken ook bekend als Twee fasenbemonstering. Het nut van het tweede monster ligt waarin het helpt om precies de schatting van de redenen en regressies van een bepaalde hulpvariabele te bepalen, die ontstaat in het licht van de analyse van een eerste monster.

Een ander gebruik dat aan de dubbele bemonstering wordt gegeven, is om informatie te verzamelen voor het realiseren van een lagenbemonstering.

Voorbeelden

Hieronder staan ​​verschillende situaties waarin dubbele bemonstering gerechtvaardigd is.

Kwaliteitscontrole bij de uitwerking van stukken

De dubbele bemonsteringsmethode wordt vaak gebruikt in de regeling van industriële kwaliteit en wordt meestal in twee fasen gedaan.

Stel bijvoorbeeld dat een industriële machine die bepaalde stukken voorbereidt. Zoveel als de machine wordt aangepast, is geen stuk identiek aan een ander, omdat in zijn afmetingen en gewicht kleine variaties kunnen optreden. Het gaat erom te bepalen of veel onderdelen worden vervaardigd door die machine voldoet aan de tolerantiecriteria zodat het wordt geaccepteerd of afgewezen.

Eerst wordt een willekeurig voorbeeld van stukken genomen waarmee een van de variabelen moet worden gecontroleerd, bijvoorbeeld de lengte van het stuk, bevindt zich in de tolerantie.

In het geval dat de gemiddelde lengte lager is dan of boven de gewenste mate van tolerantie voor die variabele, in dit eerste monster, wordt dan afgeleid dat de partij defect is en moet het worden weggegooid. In dit geval is het niet vereist om nieuwe monsters te nemen.

Kan u van dienst zijn: Correlatiecoëfficiënt: formules, berekening, interpretatie, voorbeeld

Integendeel, als de gemiddelde waarde binnen het tolerantiebereik ligt, maar de standaardafwijking van het monster groot genoeg is voor de som of aftrekking met de gemiddelde waarde is buiten de marge, dan is het nodig om een ​​tweede hoofdmonster te verzamelen.

Deze tweede steekproef moet de oorspronkelijke steekproef bevatten om de berekeningen opnieuw te doen en dus een definitieve beslissing te nemen met betrekking tot de onderzochte variabele. Op deze manier kan het bekend zijn of de kavel defect is of niet.

Verlaging van de bemonsteringskosten

Bij vele gelegenheden is informatie over een van de variabelen die u wilt bestuderen moeilijk toegankelijk te zijn. Maar er kan een hulpvariabele gemakkelijker zijn voor het verzamelen van gegevens.

In dit geval worden twee monsters genomen, een grote voor de hulpvariabele, minder duur en een klein monster, opgenomen in het belangrijkste monster van de duurste variabele.

Deze methode is van toepassing wanneer wordt vastgesteld dat er een verband bestaat tussen beide variabelen, wat in het algemeen een evenredigheidsrelatie is.

Een voorbeeld van deze situatie verschijnt in de boswetenschappen, waar het gewenst is om het percentage bomen te bepalen dat wordt getroffen door een parasietplant (La Tiña).

Aangezien deze zeer uitgebreid zijn en moeilijk toegang tot regio's zijn, is de volledige populatie bomen onhaalbaar in tijd en kosten. Deze stappen worden vervolgens gevolgd:

Stap 1: bemonstering

Voorlopige bemonstering zou bestaan ​​uit het gebruik van luchtfotografie en het bos is onderverdeeld in kavels. Een paar kavels worden willekeurig gekozen en geschat, door analyse van de beelden van de gekozen kavels, hoeveel bomen worden beïnvloed door de ringworm, omdat de kleur van de bomen wordt beïnvloed door de parasiet.

Kan u van dienst zijn: Euclid Stelling

Stap 2: Veldwerk

Maar fotografische analyse kan niet nauwkeurig zijn, dus gaan we door, bij voorkeur willekeurig, een paar veel van het eerste voorbeeld dat een veldwerk doet.

Stap 3: Vergelijking

Dan wordt het veldresultaat vergeleken met de fotografische voor de onderschepping van de twee veel kavels. Deze vergelijking kan bijvoorbeeld worden uitgevoerd, het maken van een grafiek waarin de horizontale as de waarde is die voor elke partij wordt verkregen door fotografie en in de verticale as de waarde verkregen door lot via veldwerk.

Deze grafische methode maakt het mogelijk visueel te identificeren of er een verband is tussen de twee resultaten en bepaald, door een regressieanalyse, de evenredigheid of verhouding coëfficiënt tussen de twee monsters.

Na het belangrijkste monster, dat wil zeggen het fotografische monster, wordt de gemiddelde waarde van geïnfecteerde bomen en de standaardafwijking genomen. Maar omdat de evenredigheidscoëfficiënt en de fout ervan met de veldmonsters werden bepaald, is het mogelijk om het resultaat van het belangrijkste monster (de fotografische) te corrigeren).

Dan kan dit resultaat worden geëxtrapoleerd naar de volledige populatie bomen.

Voor- en nadelen van dubbele bemonstering

In de beschreven voorbeelden is het kostenvoordeel bewijs.

Een nadeel is dat, in het geval van dubbele bemonstering voor kwaliteitscontrole, er een risico bestaat om veel veel producten te doorlopen die uit tolerantie zijn.

Oefening

U wilt het aantal zieke bomen schatten in een bos van 162 hectare. Omdat het bos zeer uitgebreid is, is het onderverdeeld in 100 plots van hetzelfde gebied. 18 plots worden willekeurig gekozen en door een fotografische studie worden ze geschat dat er in die 18 plots 8 zieke bomen zijn met een standaardfout van ongeveer 4,5 bomen.

Kan u van dienst zijn: wat zijn de delen van de breuk? (Voorbeelden)

Van deze 18 plots worden 8 percelen willekeurig gekozen. Voor die acht plots resulteert de fotografische studie in 10 zieke bomen met een fout van min of meer 5,3 bomen.

Aan de andere kant gooit voor diezelfde acht plots de veldstudie 12,4 zieke bomen met een fout van meer dan 6,3 bomen.

Het wordt gevraagd:

• a) Bepaal de evenredigheidscoëfficiënt tussen de veldstudie door lineaire regressie.
• b) Schat het aantal zieke bomen via de fotografische methode in de honderd plots.
• c) Pas de correctie toe met de verkregen evenredigheidscoëfficiënt om het reële aantal zieke bomen in het hele bos te schatten.

Oplossing

Een grafiek van het aantal bomen per fotografische telling versus veldtelling voor de acht kavels geselecteerd voor beide studies.

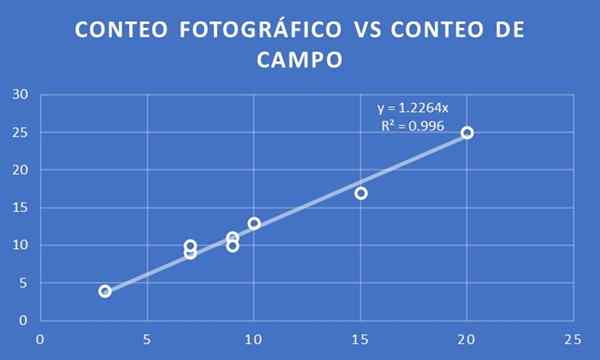Fotografische telling versus veldtelling. Bron: f. Zapata.

Een trendlijn wordt aangepast en de helling is bepaald. In dit geval wordt verkregen dat de evenredigheidscoëfficiënt 1,23 is. Dat wil zeggen, als X het aantal fotografische telling is, wordt dan geschat dat het veldtelling y = 1,23 x zal zijn.

Het aantal zieke bomen volgens de fotografische telling in de 18 geselecteerde partijen zal zijn:

18 x 8.5 = 153

Maar omdat het hele bos was verdeeld in 100 plots van hetzelfde gebied, is het aantal ziektebomen dat is geschat door de fotografische methode: (100/18) x 153 = 850.

De correctiefactor verkregen uit de vergelijking tussen het veld en de fotografische studie wordt nu toegepast:

Geschat reëel aantal zieke bomen in het bos = 1,23 x 850 = 1046.

Referenties

1. Dubbele steekproef voor ratio -schatting, Pennstate College. Opgehaald van PSU.Edu
2. Dubbel, meervoudige en segential sampling, NC State University. Hersteld van NCSU.Edu
3. Eenvoudige willekeurige bemonstering. Teruggewonnen van Investopedia.com
4. Wat is dubbele bemonstering? Hersteld van: nist.Gov
5. Steekproef. Opgehaald uit: in.Wikipedia.borg
6. Meerstaps monster. Opgehaald uit: in.Wikipedia.borg