Opgebouwde frequentieformule, berekening, verdeling, voorbeelden

De opgebouwde frequentie Het is de som van absolute frequenties f, van het kind waarmee overeenkomt met een bepaalde waarde van de variabele. Op zijn beurt is de absolute frequentie het aantal keren dat een observatie verschijnt in de gegevensset.

Het is duidelijk dat de onderzoeksvariabele ordelijk moet zijn. En omdat de opgebouwde frequentie wordt verkregen door de absolute frequenties toe te voegen, blijkt dat de opgebouwde frequentie naar de laatste gegevens moet samenvallen met het totale aantal van hen. Anders is er een fout in de berekeningen.

De verzamelde frequentie wordt gebruikt bij het beheer van statistische gegevens

Over het algemeen wordt de opgebouwde frequentie aangeduid als F_Je (Of soms n_Je), om het te onderscheiden van de absolute frequentie f_Je en het is belangrijk om er een kolom voor toe te voegen in de tabel waarmee de gegevens worden georganiseerd, bekend als Frequentietabel.

Op deze manier wordt het onder andere vergemakkelijkt om het verslag van te houden van hoeveel gegevens zijn geteld tot bepaalde observatie.

A F_Je Het staat ook bekend als Absolute opgebouwde frequentie. Als u zich verdeelt tussen de totale gegevens, heeft u de Relatieve opgebouwde frequentie, wiens uiteindelijke som gelijk moet zijn aan 1.

[TOC]

Formules

De opgebouwde frequentie van een bepaalde waarde van variabele x_Je  Het is de som van de absolute frequenties F van alle waarden lager dan of gelijk aan het:

F_Je  = f₁ + F₂ + F₃  +… F_Je

Door alle absolute frequenties toe te voegen, wordt het totale aantal gegevens n verkregen, dat wil zeggen:

F₁ + F₂ + F₃ +.. . + F_N = N

De vorige bewerking is op een samenvattende manier geschreven door het somsymbool ∑:

∑ f_Je = N

Andere opgebouwde frequenties

De volgende frequenties kunnen ook worden verzameld:

-Relatieve frequentie: Het wordt verkregen door de absolute frequentie f te delen_Je Tussen de totale gegevens n:

F_R = f_Je / N

Als de relatieve frequenties van het kind worden toegevoegd aan degene die overeenkomt met een bepaalde observatie, de verzamelde relatieve frequentie. De laatste waarde moet gelijk zijn aan 1.

-Gecumuleerd geaccumuleerd frequentiepercentage: De geaccumuleerde relatieve frequentie per 100% wordt vermenigvuldigd.

F_Reken = (f_Je / N) x 100%

Deze frequenties zijn nuttig om gegevensgedrag te beschrijven, bijvoorbeeld door het vinden van centrale neigingsmaatregelen.

Hoe u de opgebouwde frequentie kunt krijgen?

Om de opgebouwde frequentie te krijgen, is het noodzakelijk om de gegevens te bestellen en te organiseren in een frequentietabel. De procedure wordt geïllustreerd in de volgende praktische situatie:

Kan u van dienst zijn: samengestelde opvolging

-In een online winkel die mobiele telefoons verkoopt, de verkooprecord van een bepaald merk van de maand maart, de volgende waarden per dag:

1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3

De variabele is de Aantal telefoons dat per dag wordt verkocht En het is kwantitatief. De gepresenteerde gegevens zijn niet zo gemakkelijk te interpreteren, bijvoorbeeld de eigenaren van de winkel kunnen geïnteresseerd zijn om te weten of er enige trend is, zoals dagen van de week waarin de verkoop van dat merk groter is.

Informatie als deze en meer kan deze worden verkregen door de gegevens op een ordelijke manier te presenteren en de frequenties op te geven.

Hoe u de frequentietabel vult

Om de geaccumuleerde frequentie te berekenen, worden de gegevens geordend:

 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5

Vervolgens wordt een tabel met de volgende informatie gebouwd:

-De eerste kolom links met de hoeveelheid verkochte telefoons, tussen 0 en 5 en in toenemende volgorde.

-Tweede kolom: absolute frequentie, het aantal dagen dat werd verkocht 0 telefoons, 1 telefoon, 2 telefoons enzovoort.

-Derde kolom: de opgebouwde frequentie, bestaande uit de som van de vorige frequentie plus de frequentie van de te overwegen gegevens.

Deze kolom begint met de eerste kolom van de absolute frequentiekolom, in dit geval is deze 0. Voor de volgende waarde wordt dit toegevoegd met de vorige. Aldus worden de laatste gegevens van de opgebouwde frequentie voortgezet, die moeten samenvallen met de totale gegevens.

Tabel van frecuentie

De volgende tabel toont het variabele "aantal telefoons dat op één dag wordt verkocht", de absolute frequentie en de gedetailleerde berekening van de opgebouwde frequentie.

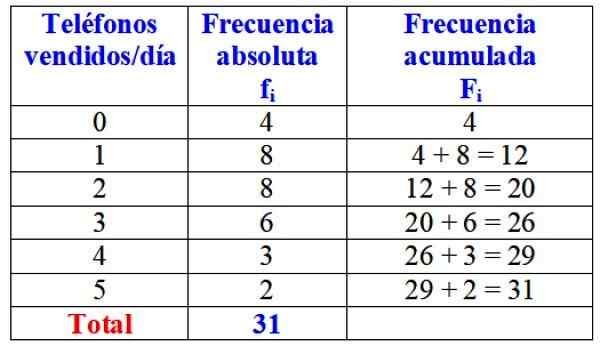Tabel met absolute en geaccumuleerde frequenties voor de variabele "telefoons die per dag worden verkocht". Bron: f. Zapata.

Op een eerste gezicht kan worden gezegd dat het merk in kwestie bijna altijd een of twee telefoons per dag wordt verkocht, omdat de meest absolute frequentie 8 dagen is, wat overeenkomt met deze waarden van de variabele. Slechts 4 dagen van de maand verkocht geen enkele telefoon.

Het kan u van dienst zijn: trigonometrische redenen: voorbeelden, oefeningen en toepassingen

Zoals opgemerkt, is het gemakkelijker om de tabel te onderzoeken dan de losse gegevens die oorspronkelijk zijn verzameld.

Opgebouwde frequentieverdeling

Een geaccumuleerde frequentieverdeling is een tabel waar absolute frequenties, geaccumuleerde frequenties, geaccumuleerde relatieve frequenties en geaccumuleerde procentuele frequenties beschikbaar zijn.

Hoewel het voordeel van het organiseren van de gegevens in een tabel zoals de vorige wordt opgemerkt, als het gegevensnummer erg groot is, is het mogelijk dat het niet voldoende is om ze te organiseren zoals hierboven weergegeven, want als veel frequenties verschijnen, is het nog steeds moeilijk interpreteren.

Het probleem kan worden opgelost door een Frequentieverdeling Met intervallen, een nuttige procedure wanneer de variabele een groot aantal waarden nodig heeft of als deze een continue variabele is.

Hier zijn de waarden gegroepeerd in intervallen van gelijke amplitude, genoemd klas. Klassen worden gekenmerkt door te hebben:

-Klasse limiet: zijn de extreme waarden van elk interval, er zijn er twee, de bovengrens en de ondergrens. Over het algemeen behoort de bovengrens niet tot het interval, maar tot de onmiddellijke aanhang, terwijl de ondergrens erbij hoort.

-Klasmerk: Het is het middelpunt van elk interval en wordt beschouwd als de representatieve waarde ervan.

-Klasbreedte: Het wordt berekend door de waarde van de major en de kleinste (bereik) af te trekken en te delen door het aantal klassen:

Klasbreedte = bereik / aantal klassen

Dan is de uitwerking van de frequentieverdeling gedetailleerd.

Voorbeeld

Deze gegevensset komt overeen met 40 graden van een wiskunde -examen, op de schaal van 0 tot 10:

0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.

Een frequentieverdeling met een bepaalde hoeveelheid klassen kan worden ontwikkeld, bijvoorbeeld 5 klassen. Er moet rekening mee worden gehouden dat bij het gebruik van vele klassen de gegevens niet gemakkelijk te interpreteren zijn en het gevoel van het uitvoeren van de groep verloren is gegaan.

Kan u van dienst zijn: hoeveel moet u toevoegen aan 3/4 om 6/7 te krijgen?

En als ze daarentegen in zeer weinig zijn gegroepeerd, wordt de informatie verdund en is een deel ervan verloren. Het hangt allemaal af van de hoeveelheid gegevens die u heeft.

In dit voorbeeld is het een goed idee om twee scores in elk interval te hebben, omdat er 10 scores zijn en er 5 klassen worden gemaakt. De rang is de aftrekking tussen de major en de kleinste beoordeling, waarbij de klassenbreedte is:

Klasse breedte = (10-0)/5 = 2

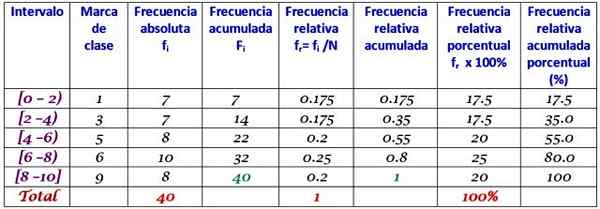
De intervallen worden links gesloten en rechts open (behalve de laatste), die respectievelijk met vierkante haakjes en haakjes wordt gesymboliseerd. Ze hebben allemaal dezelfde breedte, maar het is niet verplicht, hoewel de meest voorkomende.

Elk interval bevat een bepaalde hoeveelheid elementen of absolute frequentie, en in de volgende kolom is de opgebouwde frequentie, waarbij de som wordt gedragen. De tabel toont ook de relatieve frequentie f_R  (absolute frequentie tussen het totale aantal gegevens) en het percentage frequentiepercentage F_R × 100%.

Voorgestelde oefening

Een bedrijf belde dagelijks naar zijn klanten tijdens de eerste twee maanden van het jaar. De gegevens zijn als volgt:

6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 13, 17, 14, 26, 7, 12, 24, 7, 7

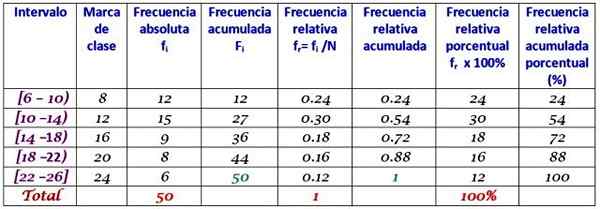
Groep in 5 klassen en bouw de tabel met de frequentieverdeling.

Antwoord

De klasbreedte is:

(26-6)/5 = 4

Probeer het op te lossen voordat u het antwoord ziet.

Referenties

1. Berenson, m. 1985. Statistieken voor administratie en economie. Inter -American S.NAAR.
2. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
3. Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.
4. Waarschijnlijkheid en statistieken. Klasse intervalbreedte. Opgehaald uit: pedroprobability en stadistisch.Blogspot.com.
5. Spiegel, m. 2009. Statistieken. Schaum -serie. 4 TA. Editie. McGraw Hill.
6. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.