Tachtenberg -methode wat is voorbeelden

Hij Trachtenberg -methode Het is een systeem om rekenkundige bewerkingen uit te voeren, voornamelijk vermenigvuldiging, op een gemakkelijke en snelle manier, zodra hun regels bekend zijn en gedomineerd zijn.

Hij werd bedacht door de Russische ingenieur Jakow Trachtenberg (1888-1953) toen hij een gevangene van de nazi's was in een concentratiekamp, ​​als een vorm van afleiding om gezond verstand te behouden terwijl hij in gevangenschap doorging.

Figuur 1. Vermenigvuldigingstabellen. Bron: Wikimedia Commons. Taulacat [cc by-sa 3.0 (https: // creativeCommons.Org/licenties/by-sa/3.0)] [TOC]

Wat is voor- en nadelen

Het voordeel dat deze methode vertegenwoordigt, is dat het niet nodig is om vermenigvuldigingen uit te voeren.

Het nadeel is dat er geen universele regel is om zich met een figuur te vermenigvuldigen, maar de regel varieert volgens de multiplier. Patronen zijn echter niet moeilijk te onthouden en staan ​​in principe bewerkingen zonder papier en potlood toe.

In dit artikel zullen we ons concentreren op de regels om zich snel te vermenigvuldigen.

[TOC]

Voorbeelden

Om de methode toe te passen is het noodzakelijk om de regels te kennen, dus we zullen ze een voor een en met voorbeelden presenteren:

- Vermenigvuldig een figuur met 10 of 11

Vermenigvuldigingsregel met 10

-Om elk figuur met 10 te vermenigvuldigen, wordt een nul eenvoudig aan de rechterkant toegevoegd. Bijvoorbeeld: 52 x 10 = 520.

Regels om te vermenigvuldigen met 11

-Een nul wordt aan het begin en aan het einde van de figuur toegevoegd.

-Elk cijfer wordt toegevoegd met zijn buur met de rechterhandige en het resultaat is onder het overeenkomstige cijfer van de oorspronkelijke figuur geplaatst.

-Als het resultaat hoger is dan negen, wordt de eenheid opgemerkt en wordt een klein punt geplaatst om te onthouden dat we een eenheid dragen die zal worden toegevoegd in de som van de volgende figuur met zijn rechterhandige buurman.

Gedetailleerd vermenigvuldigingsvoorbeeld door 11

Vermenigvuldig 673179 met 11

Kan u van dienst zijn: Convergence Radio: Definitie, voorbeelden en oefeningen opgelost

06731790 x 11 =

--

= 7404969

De benodigde stappen om dit resultaat te bereiken, geïllustreerd door kleuren, zijn de volgende:

-De 1 van de multiplierseenheid (11) werd vermenigvuldigd met de vermenigvuldiger 9 (06731790) en het werd toegevoegd 0. Het eenheidscijfer werd verkregen: 9.

-Dan vermenigvuldigt het 1 met 7 en voegt er negen toe 16 en we hebben 1, het dozijn cijfer wordt geplaatst: 6.

-Vermenigvuldiging 1 met 1 wordt vervolgens de buur van de rechter 7 plus 1 toegevoegd die daardoor leidde 9 Voor de honderd.

-De volgende figuur wordt verkregen van het vermenigvuldigen van 1 met 3 plus naburige 1, het resulteert 4 Voor het cijfer van duizenden.

-Het wordt vermenigvuldigd 1 met 7 en de buur is toegevoegd als gevolg van 10, nul wordt geplaatst (0) als tiende cijfer en het kost er een.

-Dan is 1 voor 6 plus buur 7 13 plus een 1 die 14 was, de 4 als een cijfer van de honderdduizenden en duurt 1.

-Eindelijk vermenigvuldig 1 met de nul die aan het begin werd toegevoegd, waardoor nul de buurman 6 plus een meer kreeg die nam. Het is eindelijk 7 Voor het cijfer dat overeenkomt met de miljoenen.

- Vermenigvuldiging door getallen van 12 tot 19

Om te vermenigvuldigen met 12 elk figuur: 

-Een nul wordt aan het begin toegevoegd en nog een nul aan het einde van de figuur om te vermenigvuldigen.

-Elk cijfer wordt verdubbeld van de te vermenigvuldigen figuur en voegt toe met zijn rechterhandige buurman.

-Als de som meer dan 10 is, wordt een eenheid toegevoegd aan de volgende duplicatiebewerking en voegt u toe met de buurman.

Voorbeeld van vermenigvuldiging met 12

Vermenigvuldig 63247 met 12

0632470 x 12 =

-

758964

De details om dit resultaat te bereiken, strikt volgens de uiteengezette regels, worden in de volgende figuur weergegeven:

Figuur 2. Trachtenberg -methode om elk getal met 12 te vermenigvuldigen. Bron: f. Zapata.

- Uitbreiding van de regels voor vermenigvuldigingen met 13, ... tot 19

De methode voor vermenigvuldiging met 12 kan worden uitgebreid tot vermenigvuldiging met 13, 14 tot 19 eenvoudigweg de duplicatieregel wijzigen voor het geval van de dertien, viervoudig in het geval van 14 enzovoort tot het bereikt 19.

Kan u van dienst zijn: orthogonale matrix: eigenschappen, demonstratie, voorbeelden

Regels voor producten tegen 6, 7 en 5

- Vermenigvuldiging met 6

-Voeg nullen toe aan het begin en einde van de figuur die moet worden vermenigvuldigd met 6.

-Voeg de helft van zijn rechts aan de rechterkant aan elk cijfer toe, maar als het cijfer vreemd is om bovendien 5 toe te voegen.

figuur 3. Vermenigvuldiging van een figuur met 6, volgens de Trachtenberg -methode. Bron: f. Zapata.

- Vermenigvuldiging met 7

-Voeg nullen toe aan het begin en aan het einde van de figuur om te vermenigvuldigen.

-Dupliceer elk cijfer en voeg de onderste gehele helft van de buur toe, maar als het cijfer bovendien 5 is toegevoegd.

Voorbeeld van vermenigvuldiging met 7

-Vermenigvuldig 3412 met 7

-Het resultaat is 23884. Om de regels toe te passen, wordt het eerst aanbevolen om de vreemde cijfers te herkennen en een kleine 5 te plaatsen om te onthouden dat dit cijfer aan het resultaat toevoegt.

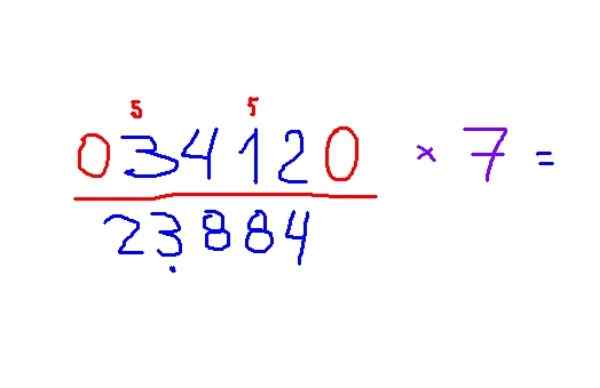Figuur 4. Voorbeeld vermenigvuldiging van een figuur met 7, volgens de methode van Trachtenberg. Bron: f. Zapata.

- Vermenigvuldiging met 5

-Voeg nullen toe aan het begin en aan het einde van de figuur om te vermenigvuldigen.

-Plaats onder elk cijfer de onderste helft van de buur rechts aan de rechterkant, maar als het cijfer vreemd is.

Voorbeeld van vermenigvuldiging met 5

Vermenigvuldig 256413 met 5

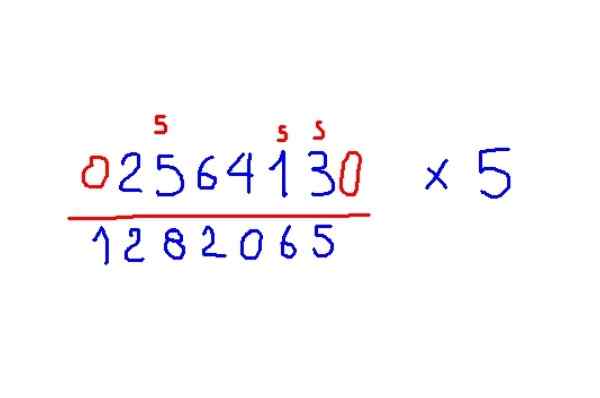Figuur 5. Voorbeeld vermenigvuldiging van een figuur met 5, volgens de traeuwtenberg -methode. Bron: f. Zapata.

Regels voor producten tegen 9

-Een nul wordt aan het begin toegevoegd en een andere aan het einde van de figuur om zich met negen te vermenigvuldigen.

-Het eerste cijfer naar rechts wordt verkregen door het af te trekken van het overeenkomstige cijfer van de figuur om te vermenigvuldigen.

-Dan wordt het volgende cijfer afgetrokken en wordt de buurman toegevoegd.

-De vorige stap wordt herhaald totdat u nul van het vermenigvuldigen bereikt, waarbij we 1 van de buur aftrekken en het resultaat wordt gekopieerd onder de nul.

Kan u van dienst zijn: wat zijn de delers van 30? (Uitleg)

Voorbeeld van vermenigvuldiging met 9

Vermenigvuldig 8769 met 9:

087690 x 9 =

--

78921

Activiteiten

10 - 9 = 1

(9-6) + 9 = 12 (De 2 En het duurt 1)

(9-7)+1+6 =9

(9-8) +7 =8

(8-1) = 7

Vermenigvuldiging met 8, 4, 3 en 2

-Voeg nullen toe aan het begin en aan het einde van de figuur om te vermenigvuldigen.

-Voor het eerste cijfer aan de rechterkant trekt u af van 10 en het resultaat wordt verdubbeld.

-Voor de volgende cijfers trekken af ​​van 9, het resultaat wordt verdubbeld en de buur wordt toegevoegd.

-Bij het bereiken van nul aftrek 2 van rechts rechts.

- Vermenigvuldiging met 8

Voorbeeld van vermenigvuldiging met 8

-Vermenigvuldig 789 met 8

Figuur 6. Voorbeeld vermenigvuldiging van een figuur met 8, volgens de traeuwtenberg -methode. Bron: f. Zapata.

- Vermenigvuldiging met 4

-Voeg nullen naar rechts en links van vermenigvuldiging toe.

-Trek af van 10 het overeenkomstige cijfer van het apparaat dat 5 toevoegt als het een oneven cijfer is.

-Trek af van 9 in de vorm van elk vermenigvuldigende cijfer, voeg de helft van de buurman aan de rechterkant toe en als het een oneven cijfer is om bovendien 5 toe te voegen.

-Bij het bereiken van nul aan het begin van het vermenigvuldigende plaats helft van de buurman behalve één.

Voorbeeld van vermenigvuldiging met 4

Vermenigvuldig 365187 x 4

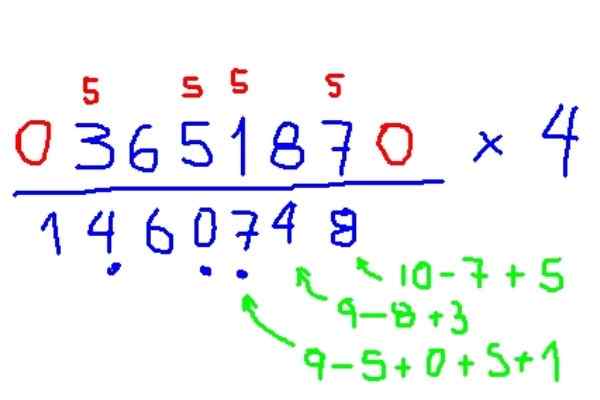Figuur 7. Voorbeeld vermenigvuldiging van een figuur met 4, volgens de traeuwtenberg -methode. Bron: f. Zapata.

- Vermenigvuldiging met 3

-Voeg nul toe aan elk uiteinde van het vermenigvuldigen.

-Trek 10 af, behalve het cijfer van het apparaat en voeg 5 toe als het een oneven cijfer is.

-Voeg voor de andere cijfers 9 het resultaat af, voeg de helft van de buurman toe en voeg 5 toe als het vreemd is.

-Plaats bij het bereiken van nul van de kopbal de hele helft van de buurman min 2.

Voorbeeld van vermenigvuldiging met 3

Vermenigvuldig 2588 met 3

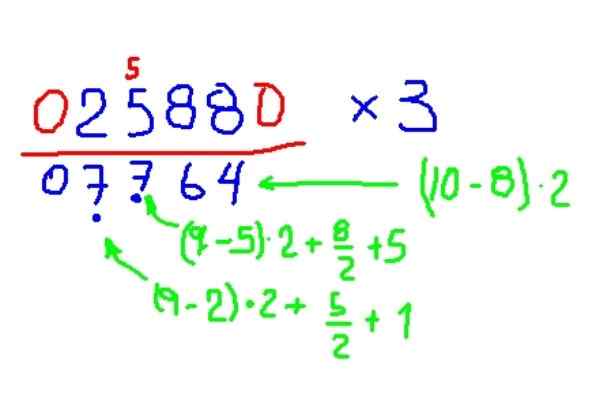Figuur 8. Voorbeeld vermenigvuldiging van een figuur met 3, volgens de traeuwtenberg -methode. Bron: f. Zapata.

- Vermenigvuldiging met 2

-Voeg nullen toe aan de uiteinden en verdubbel elk cijfer, als u 10 overschrijdt, voeg er een toe aan de volgende.

Voorbeeld van vermenigvuldiging met 2

Vermenigvuldig 2374 met 2

023740 x 2

04748

Vermenigvuldig door samengestelde figuren

De hierboven vermeende regels worden toegepast, maar de resultaten lopen links het aantal plaatsen dat overeenkomt met tientallen, honderden enzovoort. Laten we eens kijken naar het volgende voorbeeld:

Oefening 

Vermenigvuldig 37654 met 498

0376540 x 498

301232 regel voor 8

338886 Regel voor 9

150616 Regel voor 4

18751692 Laatste som

Referenties

1. Cutler, Ann. 1960.Het Tachtenberg -snelheidssysteem van basiswiskunde. Doubleday & Co, NY.
2. Dialnet. Snelle fundamentele wiskundesysteem. Hersteld van: dialnet.com
3. Wiskundige hoek. Snelle vermenigvuldiging door de methode van Trachtenberg. Hersteld van: Rinconmathematical.com
4. Het Tachtenberg -snelheidssysteem van basiswiskunde. Hersteld van: TrachtenbergspeedMath.com
5. Wikipedia. Trachtenberg -methode. Hersteld van: Wikipedia.com