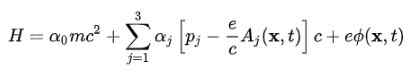Aomic model van Dirac Jordan -kenmerken en postulaten

Hij Dirac-Jordan Atomic Model Het is de relativistische generalisatie van de Hamiltoniaanse operator in de vergelijking die de Quantum Wave -functie beschrijft. In tegenstelling tot het voorgaande model, dat van Schrodinger, is het niet nodig om de spin door het uitsluitingsprincipe van Pauli op te leggen, omdat het van nature verschijnt.

Bovendien bevat het Dirac-Jordan-model relativistische correcties, spin-organ interactie en Darwin's term, die de fijne structuur van de elektronische niveaus van het atoom verklaren.

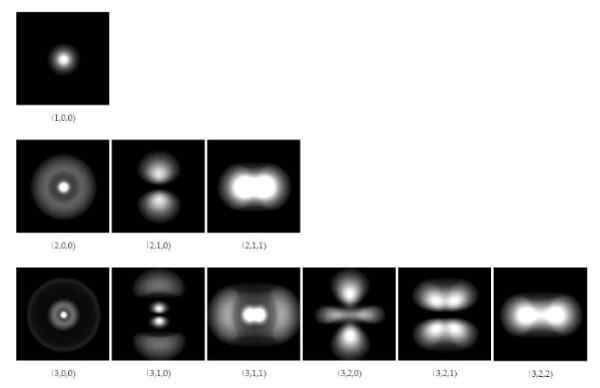
Figuur 1. Elektronische orbitalen in het waterstofatoom voor de eerste drie energieniveaus. Bron: Wikimedia Commons.

Vanaf 1928, wetenschappers Paul A. M. Dirac (1902-1984) en Pascual Jordan (1902-1980), werden voorgesteld om de kwantummechanica te generaliseren die door Schrodinger is ontwikkeld, om de correcties van de speciale relativiteitstheorie van Einstein op te nemen.

Dirac -deel van de Schrodinger -vergelijking, die bestaat uit een differentiaaloperator, genaamd Hamiltonian, die werkt op een functie die bekend staat als bekend De elektronengolffunctie. Schrodinger hield echter geen rekening met de relativistische effecten.

Wegfunctieoplossingen maken het mogelijk om de gebieden te berekenen waar het elektron rond de kern met een zekere mate van waarschijnlijkheid zal worden gevonden. Deze regio's of gebieden worden genoemd Orbitalen En ze zijn afhankelijk van bepaalde discrete kwantumaantallen, die de energie en het hoekmomentum van het elektron definiëren. 

[TOC]

Postuleren

In kwantummechanische theorieën, of het nu relativistisch is of niet, is er geen concept van banen, omdat noch de positie noch de snelheid van het elektron tegelijkertijd kan worden gespecificeerd. En bovendien leidt het specificeren van een van de variabelen tot totale onnauwkeurigheid in de andere.

Hamiltonian is van zijn kant een wiskundige operator die werkt op de kwantumgolffunctie en is gebouwd uit elektronenenergie. Een vrij elektron heeft bijvoorbeeld totale energie en dat hangt af van het lineaire momentum P dus:

E = (P²)/ 2m

Om de Hamiltoniaan te bouwen, begint het bij deze uitdrukking en wordt het vervangen P Door de kwantumoperator voor het momentum: 

P = -I ħ ∂ /∂R 

Het is belangrijk op te merken dat de voorwaarden P En P Ze zijn anders, omdat de eerste het momentum is en de andere is de Differentiaaloperator geassocieerd met momentum. 

Kan u van dienst zijn: Atomisch model van leukipo: postulaten, beperkingen, belang

Bovendien is ik de denkbeeldige eenheid en ħ de planck -constante gedeeld door 2π, op deze manier wordt de Hamiltoniaanse operator H van het vrije elektron verkregen:

H = (ħ²/2m) ∂² /∂R² 

Om de Hamiltoniaan van het elektron in het atoom te vinden, wordt de elektroneninteractie met de kern toegevoegd: 

H = (ħ2/2m) ∂² /∂R²  - Eφ (R)

In de vorige expressie is -E de elektroneneleverkleding en φ (r) de elektrostatische potentiaal geproduceerd door de centrale kern.

Nu werkt operator H op de golffunctie ψ volgens de Schrodinger -vergelijking, die zo is geschreven:

H ψ = (i ħ ∂ /∂t) ψ

De vier postulaten van Dirac

Postulaat eerst: De relativistische golfvergelijking heeft dezelfde structuur als de golfvergelijking van Schrodinger, wat verandert is h:

H ψ = (i ħ ∂ /∂t) ψ

Tweede postulaat: De Hamiltoniaanse operator is gebouwd op basis van Einstein's energiemomentumrelatie, die als volgt is geschreven:

E = (m² C⁴ + P² C²))^1/2

In de vorige relatie, als het deeltje momentum p = 0 heeft, dan heb je de beroemde vergelijking e = mc² die de rustende energie van elke massa massa M relateert met de snelheid van licht C.

Derde postulaat: Om de Hamiltoniaanse operator te verkrijgen, wordt dezelfde kwantisatieregel gebruikt die in de Schrodinger -vergelijking wordt gebruikt:

P = -I ħ ∂ /∂R

In het begin was het niet duidelijk hoe hij met deze differentiële operator moest omgaan die in een vierkantswortel handelde, dus ging Dirac op weg om een ​​lineaire Hamiltoniaanse operator in de momentumoperator te verkrijgen en ontstond zijn vierde postulaat.

Postuleer kamer: Om van de vierkante wortel in de relativistische energieformule af te komen, stelde Dirac de volgende structuur voor E voor E²:

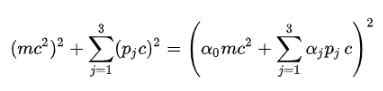
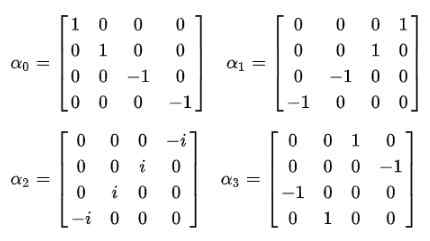
Natuurlijk is het noodzakelijk om de alfa -coëfficiënten te bepalen (α0, α1, α2, α3) zodat dit wordt vervuld.

De Dirac -vergelijking

De Dirac -vergelijking werd eerst verhoogd voor het vrije elektron, met behulp van de structuur voorgesteld in het vierde postulaat. Het blijft als volgt: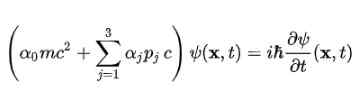

Het kan je van dienst zijn: hoor kracht: oppervlakte- en massakrachten

In zijn compacte vorm wordt de Dirac -vergelijking beschouwd als een van de mooiste wiskundige vergelijkingen ter wereld:

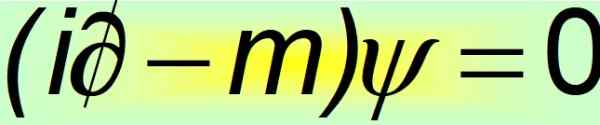Figuur 2. Dirac -vergelijking compact. Bron: f. Zapata.

En dat is wanneer wordt aangetoond dat de constante ALFA's geen scalaire hoeveelheden kunnen zijn. De enige manier waarop de gelijkheid van het vierde postulaat wordt vervuld, is dat ze 4 × 4 constante matrices zijn, die bekend staan ​​als Dirac -matrices:

Er wordt onmiddellijk opgemerkt dat de golffunctie ophoudt een scalaire functie te zijn en een vector met vier componenten wordt Spinor:

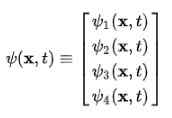
Dirac-Jordan's atoom

Om het atoommodel te verkrijgen, is het noodzakelijk om van de vrije elektronenvergelijking te gaan naar die van het elektron in het elektromagnetische veld geproduceerd door de atoomkern. Deze interactie wordt in aanmerking genomen door de potentiële scalaire φ en de potentiële vector op te nemen NAAR In de Hamiltoniaan:

De golffunctie (espinor) die het gevolg is van het opnemen van deze Hamiltoniaan heeft de volgende kenmerken: 

- Het vervult de speciale relativiteit, omdat het rekening houdt met de intrinsieke energie van het elektron (eerste term van de relativistische Hamiltoniaan)

- Het heeft vier oplossingen die overeenkomen met de vier componenten van de Espinor

- De eerste twee oplossingen komen overeen met één om +½ te spinnen en de andere met de spin - ½ 

- Ten slotte voorspellen de andere twee oplossingen het bestaan ​​van antimaterie, omdat ze overeenkomen met dat van de positronen van tegengestelden tegengestelden.

Het grote voordeel van de Dirac -vergelijking is dat de fundamentele Hamiltoniaanse correcties van Schrodinger H (O) kunnen worden opgesplitst in verschillende termen die we hieronder zullen laten zien:

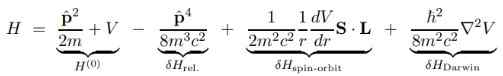
In de vorige uitdrukking is v de potentiële scalaire, omdat de potentiële vector NAAR Het is nietig als het wordt verondersteld in het centrale stationaire proton en daarom verschijnt het niet.

De reden waarom Dirac's correcties met betrekking tot Schrodinger -oplossingen in de golffunctie subtiel zijn. Ze komen voort uit het feit dat de laatste drie termen van de gecorrigeerde Hamiltoniaan allemaal worden gedeeld door de snelheid C van het vierkant, een enorm aantal, dat deze termen numeriek klein maakt.

Het kan u van dienst zijn: Vy Canis Majoris: Discovery, Kenmerken, Structuur, Training en Evolutie

Relativistische correcties voor het energiespectrum

Met behulp van de DIC-Jordan-vergelijking worden correcties gevonden in het elektronenenergiespectrum in het waterstofatoom. Er zijn ook correcties voor energie in atomen met meer dan één elektron ongeveer door een methode die bekend staat als de theorie van stoornissen.

Op dezelfde manier kunt u het Dirac -model de correctie van de fijne structuur vinden bij waterstofergieniveaus. 

Er worden echter nog meer subtiele correcties zoals de hyperfijnstructuur en de verschuiving van het lam verkregen uit meer geavanceerde modellen zoals Campos Quantum Theory, precies geboren vanwege de bijdragen van het Dirac -model.

De volgende figuur laat zien hoe Dirac's relativistische correcties op energieniveaus zijn:

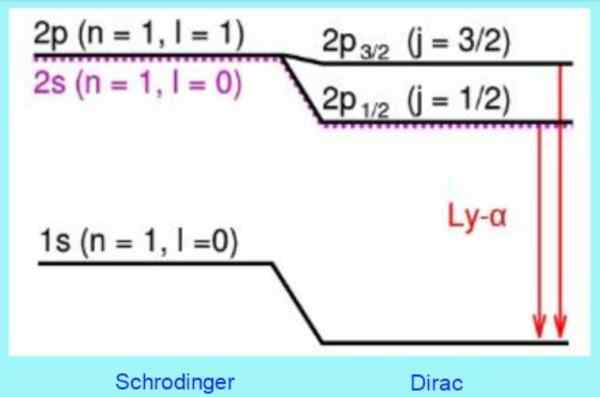figuur 3. Dirac -modelcorrecties op waterstofatoomspiegels. Bron: Wikimedia Commons.

De oplossingen voor de Dirac -vergelijking voorspellen bijvoorbeeld correct een verschuiving die is waargenomen op niveau 2s. Het is de goed bekende fijne structuurcorrectie in de Lyman -lijn - Alfa van het waterstofspectrum (zie figuur 3).

Trouwens, de fijne structuur is de naam die in atomaire fysica ontvangt het ontplooien van de lijnen van het emissiespectrum van de atomen, wat een direct gevolg is van de elektronische spin.

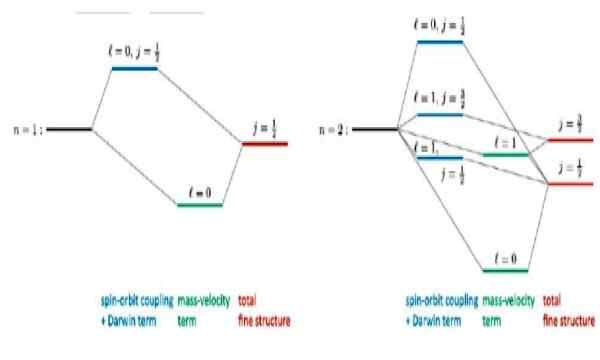Figuur 4. Fijne structuur die zich ontvouwt voor basistoestand n = 1 en de eerste geëxciteerde toestand n = 2 in het waterstofatoom. Bron: R Wirnata. Relativistische correcties voor waterstofachtige atomen. Onderzoek.netto

Interessante artikelen

Broglie Atomic Model.

Chadwick Atomic Model.

Heisenberg Atomic Model.

Perrin Atomic Model.

Thomson Atomic Model.

Dalton Atomic Model.

Schrödinger atomair model.

Democritus Atomic Model.

Leucipo -atoommodel.

Bohr Atomic Model.

Huidig ​​atoommodel.

Referenties

1. Atoom theorie. Hersteld van Wikipedia.borg.
2. Elektron magnetisch moment. Hersteld van Wikipedia.borg.
3. Quanta: A Handbook of Concepts. (1974). Oxford Universiteit krant. Hersteld van Wikipedia.borg.
4. Dirac Jordan Atomic Model. Hersteld van Prezi.com.
5. Het nieuwe kwantumuniversum. Cambridge University Press. Hersteld van Wikipedia.borg.