Variabiliteitsmaatregelen

Figuur 1.- De bekendste variabiliteitsmaatregelen. Bron: f. Zapata.

Wat zijn variabiliteitsmaatregelen?

De Variabiliteitsmaatregelen, Ook wel dispersiemaatregelen genoemd, het zijn statistische indicatoren die aangeven hoe dichtbij of op afstand de gegevens van hun rekenkundige gemiddelde worden gevonden. Als de gegevens dicht bij het gemiddelde zijn, is de verdeling geconcentreerd en als ze ver zijn, is dit een verspreide verdeling.

Er zijn veel variabiliteitsmaatregelen, een van de bekendste zijn:

• Bereik
• Gemiddelde afwijking
• Variantie
• Standaardafwijking

Deze maatregelen vullen de centrale tendensmaatregelen aan en zijn noodzakelijk om de verdeling van de verkregen gegevens te begrijpen en zoveel mogelijk informatie te extraheren.

Bereik

Het bereik of de route meet de amplitude van een gegevensset. Om de waarde ervan te bepalen, wordt het verschil tussen de hoogste waarde X gevonden_maximaal en de minste X -waarde_min:

R = x_maximaal - X_min

Als de gegevens niet los zijn maar gegroepeerd op interval, wordt het bereik berekend door het verschil tussen de bovengrens van het laatste interval en de ondergrens van het eerste interval.

Wanneer het bereik een kleine waarde is, betekent dit dat alle gegevens vrij dicht bij elkaar liggen, maar een groot bereik geeft aan dat er veel variabiliteit is. Het is duidelijk dat, afgezien van de bovengrens en de ondergrens van de gegevens, het bereik geen rekening houdt met de waarden tussen hen, dus het is niet raadzaam om het te gebruiken wanneer het gegevensnummer groot is.

Het is echter een onmiddellijke maatregel om te berekenen en heeft dezelfde gegevenseenheden, dus het is gemakkelijk om het te interpreteren.

Voorbeeld van rang

Vervolgens is de lijst beschikbaar met het aantal doelen dat in het weekend wordt gemarkeerd, in de voetbalcompetities uit negen landen:

Kan u van dienst zijn: wat zijn de delers van 30? (Uitleg)

40, 32, 35, 36, 37, 31, 37, 29, 39

Het is een gegevensset zonder te groeperen. Om het bereik te vinden, bestellen ze ze van het minst tot het beste:

29, 31, 32, 35, 36, 37, 37, 39, 40

De gegevens met de hoogste waarde zijn 40 doelen en die met de laagste waarde is 29 doelen, daarom is het bereik:

R = 40-29 = 11 doelen.

Er kan worden aangenomen dat het bereik klein is in vergelijking met de gegevens van de minimumwaarde, wat 29 doelen zijn, dus kan worden aangenomen dat de gegevens geen grote variabiliteit hebben.

Gemiddelde afwijking

Deze variabiliteitsmaat wordt berekend door het gemiddelde van de absolute waarden van de afwijkingen ten opzichte van het gemiddelde. Duidt op de gemiddelde afwijking als D_M, Voor niet -groepen gegevens wordt de gemiddelde afwijking berekend door de volgende formule:

Waarbij n het aantal beschikbare gegevens is, x_Je Het vertegenwoordigt elke gegevens en X̄ is het gemiddelde, dat wordt bepaald door alle gegevens toe te voegen en te delen tussen N:

De gemiddelde afwijking maakt het mogelijk gemiddeld te weten hoeveel eenheden de gegevens afwijken van het rekenkundig gemiddelde en heeft het voordeel dat ze dezelfde eenheden hebben als de gegevens waarmee het werkt.

Middenafwijkingsvoorbeeld

Volgens de gegevens van het bereik is het aantal gemarkeerde doelen:

40, 32, 35, 36, 37, 31, 37, 29, 39

Als u de medium D -afwijking wilt vinden_M Van deze gegevens is het noodzakelijk om eerst het X̄ -rekenkundig gemiddelde te berekenen:

En nu de waarde van X̄ bekend is, gaan we verder met het vinden van de gemiddelde afwijking_M:

= 2.99 ≈ 3 doelen

Daarom kan worden gezegd dat de gegevens gemiddeld ongeveer weggaan in 3 gemiddelde doelen die 35 doelen zijn, en zoals opgemerkt, is het een veel preciezere maatregel dan het bereik.

Kan u van dienst zijn: hyperbool

Variantie

De gemiddelde afwijking is een veel dunnere variabiliteitsmaat dan het bereik, maar zoals berekend door de absolute waarde van de verschillen tussen elke gegevens en het gemiddelde, biedt het geen grotere veelzijdigheid vanuit het algebraïsche standpunt.

Daarom heeft de variantie de voorkeur, wat overeenkomt met het gemiddelde van het kwadratische verschil van elke gegevens met het gemiddelde en wordt berekend met behulp van de formule:

In deze uitdrukking, s² geeft de variantie aan, en zoals altijd x_Je vertegenwoordigt elk van de gegevens, x̄ is het gemiddelde en n de totale gegevens.

Bij het werken met een steekproef in plaats van de populatie heeft het de voorkeur om de variantie als deze te berekenen:

Het verschil met de vorige formule is dat er in de noemer n - 1 in plaats van n zijn. Het gebeurt dat door te delen door N, de variantie van de steekproef de variantie onderschat van de populatie waaruit deze werd geëxtraheerd, maar niet wanneer deze wordt gedeeld door n - 1. In sommige teksten verschijnt die uitdrukking met de naam van quasi-variza.

In elk geval wordt variantie gekenmerkt door altijd een positieve hoeveelheid te zijn, maar als het gemiddelde van kwadratische verschillen, is het belangrijk om op te merken dat het niet dezelfde eenheden heeft als die van de gegevens.

Voorbeeld van variantie

Om de variantie van de gegevens van de voorbeelden van bereik en gemiddelde afwijking te berekenen, worden de overeenkomstige waarden vervangen en de aangegeven som. In dit geval wordt het gekozen om te delen tussen N-1:

= 13.86

Standaardafwijking

De variantie heeft niet dezelfde eenheid als die van de onderzochte variabele, bijvoorbeeld als de gegevens in meters worden geleverd, resulteert de variantie in vierkante meters. Of in het voorbeeld van de doelen zou het zijn in doelen in het kwadraat, wat nergens op slaat.

Kan u van dienst zijn: wat zijn de elementen van de gelijkenis? (Onderdelen)

Daarom wordt de standaardafwijking gedefinieerd, ook wel genoemd Typische afwijking, Zoals de vierkantswortel van de variantie:

S = √s²

Op deze manier wordt een maat voor variabiliteit van de gegevens verkregen in dezelfde eenheden als deze, en hoe lager de waarde van s, hoe meer gegroepeerd de gegevens rond het gemiddelde zijn.

Zowel de variantie als de standaardafwijking zijn de variabiliteitsmaatregelen die moeten worden gekozen wanneer het rekenkundig gemiddelde de maat is voor de centrale neiging die het gedrag van de gegevens het beste beschrijft.

En het is dat de standaardafwijking een belangrijke eigenschap heeft, bekend als de stelling van Chebyshev: ten minste 75% van de waarnemingen is in het interval gedefinieerd door X ± 2s. Met andere woorden, 75% van de gegevens is maximaal op afstand gelijk aan 2s rond gemiddeld.

Evenzo bevindt zich ten minste 89% van de waarden op een afstand van 3 seconden van het gemiddelde, een percentage dat kan worden uitgebreid, op voorwaarde dat veel gegevens beschikbaar zijn en deze volgen een normale verdeling.

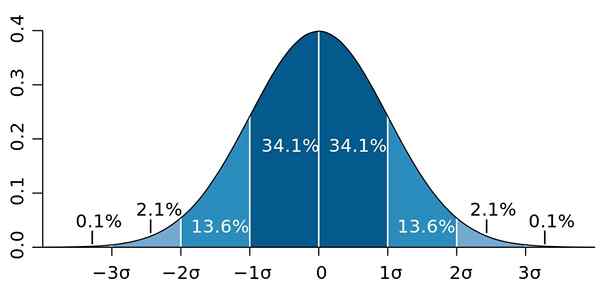
Figuur 2.- Als de gegevens een normale verdeling volgen, 95.4 van hen zijn twee standaardafwijkingen aan beide zijden van het gemiddelde. Bron: Wikimedia Commons.

Voorbeeld van standaardafwijking

De standaardafwijking van de gegevens die in de vorige voorbeelden worden gepresenteerd, is:

S = √s² = √13.86 = 3.7 ≈ 4 doelen