Distributie F -kenmerken en oefeningen opgelost

De distributie F o Visher-sedercorverdeling wordt gebruikt om de varianties van twee verschillende of onafhankelijke populaties te vergelijken, die elk een normale verdeling volgen.

De verdeling die volgt op de variantie van een set monsters van een enkele normale populatie is de ji-kwadraatverdeling (Χ²) van graad N-1, als elk van de monsters van de set N-elementen heeft.

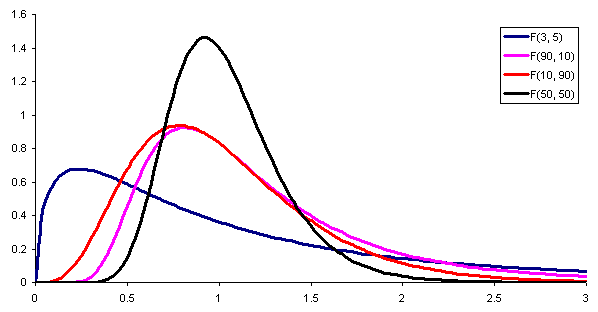
Figuur 1. Hier is de waarschijnlijkheidsdichtheid van de verdeling F met verschillende combinaties van parameters (of vrijheidsgraden) van respectievelijk teller en noemer. Bron: Wikimedia Commons.

Om de varianties van twee verschillende populaties te vergelijken, is het noodzakelijk om een statistisch, dat wil zeggen een hulpmiddel willekeurige variabele die het mogelijk maakt om te onderscheiden of beide populaties al dan niet dezelfde variantie hebben.

Deze hulpvariabele kan rechtstreeks het quotiënt zijn van de steekproefvarianties van elke populatie, in welk geval, als deze quotiënt dicht bij de eenheid ligt, wordt aangetoond dat beide populaties vergelijkbare varianties hebben.

[TOC]

De statistiek F en zijn theoretische verdeling

De willekeurige variabele f of statistische F voorgesteld door Ronald Fisher (1890 - 1962) is degene die vaker wordt gebruikt om de varianties van twee populaties te vergelijken en wordt als volgt gedefinieerd:

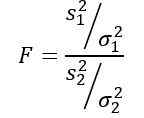
Zijn s² De voorbeeldvariantie en σ² De populatievariantie. Om elk van de twee bevolkingsgroepen te onderscheiden, worden abonnementen 1 en 2 gebruikt respectievelijk.

Het is bekend dat de Ji-kwadraatverdeling met (N-1) vrijheidsgraden degene is die de hulp (of statistische) variabele volgt die hieronder wordt gedefinieerd:

X² = (N-1) s² / σ².

Daarom volgt statistiek F een theoretische verdeling gegeven door de volgende formule:

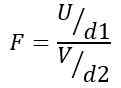
Wezen OF De ji-kwadraatverdeling met D1 = N1 - 1 vrijheidsgraden voor bevolking 1 en V De ji-kwadraatverdeling met D2 = N2 - 1 Vrijheidsgraden voor bevolking 2.

Kan u van dienst zijn: vectoralgebra

De op deze manier gedefinieerde verhouding is een nieuwe waarschijnlijkheidsverdeling, bekend als distributie F met D1 vrijheidsgraden in de teller en D2 vrijheidsgraden in de noemer.

Gemiddelde, mode en variantie van distributie f

Half

De gemiddelde verdeling F wordt als volgt berekend:

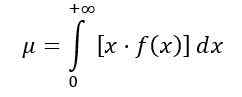
Zijnde f (x) de waarschijnlijkheidsdichtheid van verdeling f, die wordt getoond in figuur 1 voor verschillende combinaties van parameters of vrijheidsgraden.

U kunt de waarschijnlijkheidsdichtheid f (x) schrijven, afhankelijk van de γ -functie (gamma -functie):

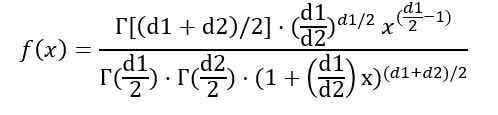
Zodra de eerder aangegeven integraal is aangegeven, wordt geconcludeerd dat het gemiddelde van de verdeling F met vrijheidsgraden (D1, D2) is: is: is: is:

μ = d2 / (d2 - 2) met d2> 2

Waar het laat zien dat het gemiddelde nieuwsgierig niet afhangt van de vrijheidsgraden D1 van de teller.

Mode

Aan de andere kant hangt mode af van D1 en D2 en wordt gegeven door:

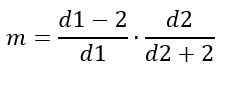
Voor d1> 2.

Variantie van de verdeling f

De variantie σ² van distributie F wordt berekend uit de integraal:

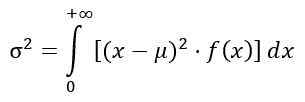
Het verkrijgen van:

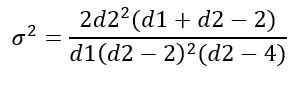
Distributiebeheer f

Net als andere continue waarschijnlijkheidsverdelingen waarbij ingewikkelde functies betrokken zijn, wordt distributie F -management gedaan door tabellen of door software.

Distributietabellen f

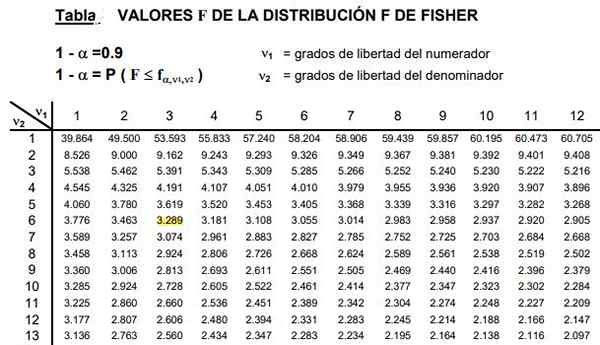Figuur 2. Een deel van de F -distributietabel wordt getoond, die meestal zeer uitgebreid zijn omdat er een brede combinatie is van mogelijke vrijheidsgraden D1 en D2.

De tabellen omvatten de twee parameters of graden van distributie.

Kan u van dienst zijn: ongelijkheid van de driehoek: demonstratie, voorbeelden, opgeloste oefeningen

Figuur 2 toont een gedeelte van de F -distributietabel voor het geval van een mate van belang 10%, dat is α = 0,1. De waarde van F wordt gemarkeerd wanneer D1 = 3 en D2 = 6 met betrouwbaarheidsniveau 1- α = 0,9 dat is 90%.

Software voor distributie F

Wat betreft de software die de distributie F beheert, is er een grote variëteit, van de spreadsheets als Uitblinken Zelfs gespecialiseerde pakketten zoals Minitab, SPSS En R Om enkele van de bekendste te noemen.

Opgemerkt moet worden dat geometrie- en wiskundesoftware Geogebra Het heeft een statistisch hulpmiddel dat de belangrijkste distributies omvat, inclusief distributie F. Figuur 3 toont de verdeling F voor geval D1 = 3 en D2 = 6 betrouwbaarheidsniveau 90%.

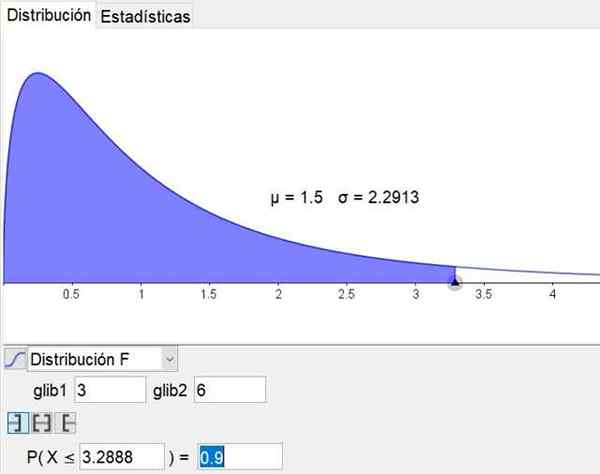figuur 3. De verdeling F wordt getoond voor geval D1 = 3 en D2 = 6 met 90%betrouwbaarheidsniveau, verkregen via het statistisch gereedschap Geogebra. Bron: Geogebra.borg

Opgeloste oefeningen

Oefening 1

Overweeg twee monsters van populaties die dezelfde populatievariantie hebben. Als monster 1 grootte N1 = 5 is en monster 2 is grootte N2 = 10, bepaal dan de theoretische waarschijnlijkheid dat de verhouding van de respectieve varianties minder is dan of gelijk aan 2.

Oplossing

Er moet aan worden herinnerd dat statistiek F wordt gedefinieerd als:

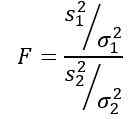
Maar ons wordt verteld dat bevolkingsvarianties hetzelfde zijn, dus voor deze oefening is het van toepassing:

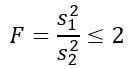
Omdat u de theoretische waarschijnlijkheid wilt weten dat deze verhouding van steekproefvarianties kleiner is dan of gelijk aan 2, moeten we het gebied kennen onder de verdeling F tussen 0 en 2, dat kan worden verkregen door tabellen of software. Hiervoor moet rekening worden gehouden met dat de vereiste verdeling F d1 = n1 - 1 = 5 - 1 = 4 en d2 = n2 - 1 = 10 - 1 = 9 heeft, dat wil zeggen de verdeling F met vrijheidsgraden (4, 9).

Het kan u van dienst zijn: serie Power: Voorbeelden en oefeningen

Door het statistische hulpmiddel van te gebruiken Geogebra Er werd vastgesteld dat dit gebied 0 is.82, dus wordt geconcludeerd dat de kans dat de verhouding van steekproefvarianties kleiner is dan of gelijk is aan 2 is 82%.

Oefening 2

Er zijn twee dunne platenproductieprocessen. De variabiliteit van de dikte moet zoveel mogelijk zijn. 21 monsters van elk proces worden genomen. Het procesmonster heeft een standaardafwijking van 1,96 micron, terwijl die van proces B standaardafwijking van 2,13 micron heeft. Welke van de processen heeft een lagere variabiliteit? Gebruik een afwijzingsniveau van 5%.

Oplossing

De gegevens zijn als volgt: SB = 2.13 met nb = 21; SA = 1,96 met NA = 21. Dit betekent dat u moet werken met een verdeling F van (20, 20) vrijheidsgraden.

De nulhypothese houdt in dat de populatievariantie van beide processen identiek is, dat wil zeggen σa^2 / σb^2 = 1. De alternatieve hypothese zou verschillende populatievarianties impliceren.

Vervolgens wordt onder de veronderstelling van identieke populatievarianties de statistiek F berekend als: fc = (sb/sa)^2 gedefinieerd.

Omdat het afstotingsiveau is genomen als α = 0,05, vervolgens α/2 = 0,025

De verdeling f (0.025; 20,20) = 0,406, terwijl f (0.975; 20,20) = 2,46.

Daarom zal de nulhypothese waar zijn als de berekende F voldoet aan: 0,406≤fc≤2,46. Anders wordt de nulhypothese afgewezen.

Als fc = (2,13/1.96)^2 = 1.18 wordt geconcludeerd dat de FC -statistiek zich in het acceptatiebereik van de nulhypothese bevindt met een zekerheid van 95%. Met andere woorden met een zekerheid van 95% hebben beide productieprocessen dezelfde populatievariantie.

Referenties

1. F Test voor onafhankelijkheid. Hersteld van: saylordotorg.Gitub.Io.
2. Med Wave. Statistieken toegepast op gezondheidswetenschappen: test F. Hersteld van: MedWave.Klet.
3. Waarschijnlijkheden en statistieken. Distributie F. Opgehaald uit: waarschijnlijkheden en estics.com.
4. Triola, m. 2012. Elementaire statistieken. 11e. Editie. Addison Wesley.
5. UNAM. Distributie F. Hersteld van: advies.Cuautitlan2.UNAM.mx.
6. Wikipedia. Distributie F. Hersteld van: is.Wikipedia.com