Positiemaatregelen, centrale neiging en dispersie

De Maatregelen van centrale, dispersie en positie neiging, Dit zijn waarden die worden gebruikt om een ​​reeks statistische gegevens correct te interpreteren. Deze kunnen direct worden bewerkt, zoals verkregen uit de statistische studie, of ze kunnen worden georganiseerd in groepen van gelijke frequentie, waardoor de analyse wordt vergemakkelijkt.

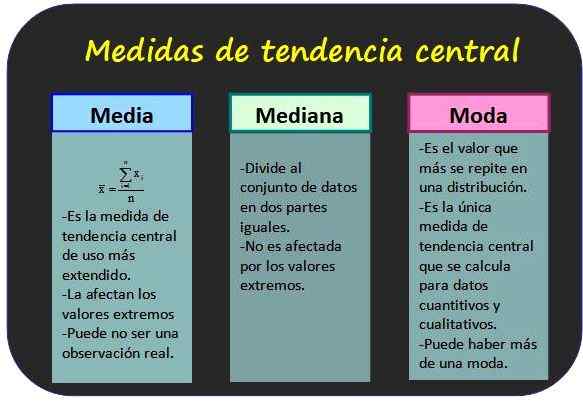
De drie bekendste centrale trendmaatregelen en enkele van zijn eigenschappen. Bron: f. Zapata.

Maatregelen van centrale neiging

Ze staan ​​toe om te weten welke waarden de statistische gegevens samen zijn gegroepeerd.

Rekenkundig gemiddelde

Het is ook bekend als het gemiddelde van de waarden van een variabele en wordt verkregen door alle waarden toe te voegen en het resultaat te delen door het totale aantal gegevens.

• Rekenkundig gemiddelde voor gegevens zonder groepering

Wees een X -variabele waarvan er geen gegevens zijn zonder te organiseren of te groeperen, het rekenkundige gemiddelde wordt als volgt berekend:

En samengevat Notatie:

Voorbeeld

De eigenaren van een bergtoeristisch hostel zijn van plan te weten hoeveel dagen gemiddeld bezoekers in de faciliteiten blijven. Om dit te doen, werd een record van de dagen van duurzaamheid van 20 groepen toeristen uitgevoerd, waarbij de volgende gegevens werden verkregen:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

De gemiddelde dagen die toeristen blijven zijn:

= 2.5 dagen

• Rekenkundig gemiddelde voor gegroepeerde gegevens

Als de variabele gegevens zijn georganiseerd in een absolute frequentietabel F_Je En klascentra zijn x₁, X₂,…, X_N, Het gemiddelde wordt berekend door:

In de samenvatting van de zomer:

Mediaan

De mediaan van een groep van n waarden van variabele X is de centrale waarde van de groep, op voorwaarde dat de waarden in toenemende mate worden geordend. Op deze manier is de helft van alle waarden lager dan mode en de andere helft is groter.

• Medium van niet -groepen gegevens

De volgende gevallen kunnen worden gepresenteerd:

-Nummer n waarden van variabele x  vreemd: De mediaan is de waarde die net in het midden van de waardengroep ligt:

-Nummer n waarden van variabele x paar: In dit geval wordt de mediaan berekend als het gemiddelde van de twee centrale waarden van de gegevensgroep:

Voorbeeld

Om de mediaan van de toeristische hostelgegevens te vinden, worden ze eerst van het minst tot de beste besteld:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Het kan u van dienst zijn: wat is de relatieve frequentie en hoe deze wordt berekend?

Het gegevensnummer is zelfs, daarom zijn er twee centrale gegevens: x₁₀ en x_elf En omdat beide 2 waard zijn, ook het gemiddelde.

Mediaan = 2

• Medium van gegroepeerde gegevens

De volgende formule wordt gebruikt:

De symbolen in de formule betekenen:

-C: Intervalbreedte met mediaan

-B_M: Lagere rand van datzelfde interval

-F_M: Aantal observaties dat het interval bevat waartoe de mediaan behoort.

-N: Totale gegevens.

-F_BM: Aantal observaties vóór het interval dat de mediaan bevat.

Mode

De mode voor niet -geëxponeerde gegevens is de meest frequentiewaarde, terwijl het voor de gegroepeerde gegevens de meest frequentieklasse is. Het wordt beschouwd als mode als de meest representatieve gegevens of distributieklasse.

Twee belangrijke kenmerken van deze maatregel zijn dat een gegevensset meer dan één mode kan hebben en mode kan worden bepaald voor zowel kwantitatieve gegevens als kwalitatieve gegevens.

Voorbeeld

Doorgaan met de gegevens van het toeristische hostel, die het meest wordt herhaald, is 1, daarom is het meest gebruikelijke ding dat toeristen 1 dag in het hostel blijven.

Dispersiemaatregelen

Dispersiemaatregelen beschrijven hoe gegroepeerd de gegevens rond de centrale maatregelen zijn.

Bereik

Het wordt berekend door de belangrijkste gegevens en de kleine gegevens af te trekken. Als dit verschil groot is, is het een teken dat de gegevens worden verspreid, terwijl de kleine waarden aangeven dat de gegevens dicht bij het gemiddelde zijn.

Voorbeeld

Het bereik voor de toeristische hostelgegevens is:

Bereik = 5-1 = 4

Variantie

• Variantie voor niet -groepen gegevens

Om de variantie te vinden² Het is noodzakelijk om eerst het rekenkundige gemiddelde te kennen, waarna het verschil wordt berekend voor het vierkant tussen elke gegevens en het gemiddelde, worden allemaal toegevoegd en gedeeld door de totale waarnemingen. Deze verschillen staan ​​bekend als afwijkingen.

De variantie, die altijd positief (of nul) is, geeft aan hoe ver de waarnemingen van het gemiddelde zijn: als de variantie hoog is, zijn de waarden meer verspreid dan wanneer de variantie klein is.

Voorbeeld

De variantie voor de gegevens van het toeristische hostel is:

1; 1; 2; 2; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; 2; 2; 3; 4; 1

= 1.95

• Variantie voor gegroepeerde gegevens

Om de variantie van een groep gegroepeerde gegevens te vinden, zijn ze vereist: i) het gemiddelde, ii) de frequentie f_Je  dat zijn de totale gegevens in elke klasse en iii) x_Je  of klassewaarde:

Het kan u van dienst zijn: soorten driehoeken

Standaardafwijking

De standaardafwijking is de positieve vierkantswortel van de variantie, dus het heeft een voordeel ten opzichte van de variantie: het komt in dezelfde eenheden als de variabele die wordt bestudeerd en heeft dus een meer direct idee dan het dichtbij of verre dat de variabele van het gemiddelde is.

• Standaardafwijking voor niet -groepen gegevens

Het wordt eenvoudig bepaald door de vierkantswortel van de variantie te vinden voor niet -gehoord gegevens:

 Voorbeeld

De standaardafwijking voor toeristische hostelgegevens is:

S = √ (s²) = √1.95 = 1.40

• Standaardafwijking voor gegroepeerde gegevens

Het wordt berekend door de vierkantswortel van de variantie voor gegroepeerde gegevens te vinden:

Positiemaatregelen

Positiemaatregelen delen een geordende set gegevens in gelijke delen. De mediaan is, naast het zijn van een centrale tendensmaatregel, ook een maat voor positie, omdat het het geheel in twee gelijke delen verdeelt. Maar u kunt kleinere onderdelen verkrijgen met kwartielen, decielen en percentielen.

Kwartiel

Kwartielen delen de set in vier gelijke delen, elk met 25 % van de gegevens. Ze worden aangeduid als Q₁, Q₂ en Q₃ En de mediaan is het kwartiel Q₂. Op deze manier bevindt 25% van de gegevens zich onder het kwartiel Q₁, 50% onder het kwartiel Q₂ of mediaan en 75% onder het kwartiel Q₃.

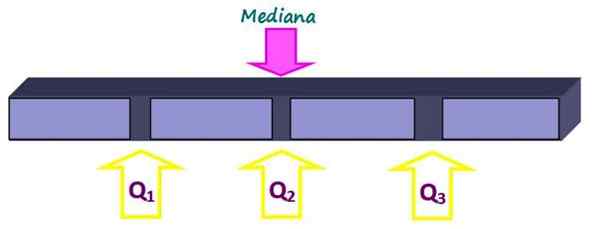Figuur 2. Kwartielen verdelen de gegevensset in vier gelijke delen. Bron: f. Zapata.

• Kwartielen voor niet -groepen gegevens

De gegevens worden geordend en het totaal is verdeeld in 4 groepen met hetzelfde aantal gegevens elk. De positie van het eerste kwartiel wordt gevonden door:

Q₁ = (n+1)/4

De totale gegevens zijn. Als het resultaat de volledige gegevens zijn die overeenkomen met die positie, maar als het decimaal is, worden de gegevens die overeenkomen met het gehele onderdeel met het volgende gemiddeld, of voor een grotere precisie is het lineair geïnterpoleerd tussen genoemde gegevens.

Voorbeeld

De positie van het eerste kwartiel Q₁ Voor de gegevens van het toeristische hostel is:

Q₁ = (n+1) / 4 = (20+1) / 4 = 5.25

Dit is de positie van kwartiel 1 en als resultaat is decimaal, worden gegevens X -gegevens gevraagd₅ en x_6, die respectievelijk x zijn₅ = 1 en x₆ = 1 en ze zijn gemiddeld, resulterend:

Eerste kwartiel = 1

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

De positie van het tweede kwartiel Q₂ is:

Kan u van dienst zijn: telescopische som: hoe het is opgelost en opgeloste oefeningen

Q₂ = 2 (n+1)/4 = 10.5

Dat is het gemiddelde tussen x₁₀ en x_elf en valt samen met de mediaan:

Tweede kwartiel = mediaan = 2

De derde kwartielpositie wordt berekend door:

Q₃ = 3 (n+1) / 4 = 3 (20+1) / 4 = 15.75

Het is ook decimaal, daarom zijn x gemiddeld_vijftien en x₁₆:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Maar zoals beide waard zijn 4:

Derde kwartiel = 4

De algemene formule voor de positie van kwartielen in niet -geholpen gegevens is:

Q_k = K (n+1)/4

Met k = 1,2,3.

• Kwartielen voor gegroepeerde gegevens

Ze worden berekend als de mediaan:

De uitleg van de symbolen is:

-B_Q: Lagere rand van het interval dat kwartiel bevat

-C: Breedte van dat interval

-F_Q: Aantal observaties bevatten het kwartielinterval.

-N: Totale gegevens.

-F_BQ: Aantal gegevens vóór het interval dat kwartiel bevat.

Deciles en percentielen

Deciles en percentielen verdelen de gegevensset in respectievelijk 10 gelijke delen en 100 gelijke delen, en hun berekening wordt analoog uitgevoerd aan die van kwartielen.

• Deciles en percentielen voor niet -groepen gegevens

Formules worden respectievelijk gebruikt:

D_k = K (n+1)/10

Met k = 1,2,3 ... 9.

Decile D₅ Het moet gelijk zijn aan de mediaan.

P_k = K (n+1)/100

Met k = 1,2,3 ... 99.

Het percentiel P_vijftig Het moet gelijk zijn aan de mediaan.

Voorbeeld

In het voorbeeld van het toeristische hostel, de positie van de D₃ is:

D₃ = 3 (20+1)/10 = 6.3

Hoe wordt een decimaal getal gemiddeld x₆ en x_7, beide gelijk aan 1:

1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5

Betekent dat 3 tienden van de gegevens onder x zijn₇ = 1 en de resterende hierboven.

• Deciles en percentielen voor gegroepeerde gegevens

De formules zijn analoog aan die van kwartielen. D wordt gebruikt om de decielen en P voor de percentielen aan te duiden en de symbolen worden op een vergelijkbare manier geïnterpreteerd:

De empirische regel

Wanneer de gegevens symmetrisch worden verdeeld en de verdeling unimodaal is, is er een regel genaamd  Empirische regel of Regel 68 - 95 - 99, Dat groepeert ze in de volgende intervallen:

• 68% van de gegevens staat in het interval:

• 95% van de gegevens staat in het interval:

• 99% van de gegevens staat in het interval:

Voorbeeld

In welk interval is 95% van de toeristische hostelgegevens?

Ze zijn in het interval: [2.5−1.40; 2.5+1.40] = [1.1; 3.9].

Referenties

1. Berenson, m. 1985. Statistieken voor administratie en economie. Inter -American S.NAAR.
2. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
3. Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.
4. Spiegel, m. 2009. Statistieken. Schaum -serie. 4 TA. Editie. McGraw Hill.
5. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.