Bepalingscoëfficiëntformules, berekening, interpretatie, voorbeelden

Hij Vastberadencoëfficiënt Het is een getal tussen 0 en 1 dat de fractie van punten (x, y) weergeeft die de aanpassingslijn volgen door regressie van een gegevensset met twee variabelen.

Het staat ook bekend als aanpassing goedheid en wordt aangeduid door r². Om het te berekenen, wordt het quotiënt genomen tussen de variantie van de ŷi -gegevens geschat door het regressiemodel en de variantie van de YI -gegevens die overeenkomen met elke XI van de gegevens.

R² = Sŷ / SY

Figuur 1. Correlatiecoëfficiënt voor vier gegevensparen. Bron: f. Zapata.

Als 100% van de gegevens zich op de regressiefunctielijn bevinden, dan is de bepalingscoëfficiënt 1.

Integendeel, als voor een gegevensset en een bepaalde aanpassingsfunctie de R -coëfficiënt R² Het blijkt gelijk te zijn aan 0.5, dan kan worden gezegd dat de aanpassing bevredigend of goed is op 50%. 

Evenzo, wanneer het regressiemodel waarden van r gooit² Minder dan 0.5 Dit geeft aan dat de gekozen aanpassingsfunctie niet naar tevredenheid aan de gegevens past, daarom nodig om te zoeken naar een andere aanpassingsfunctie.

En wanneer covariantie of de correlatiecoëfficiënt Het neigt naar nul, dan zijn de variabelen x en y van de gegevens niet gerelateerd, en daarom r² zal ook de neiging hebben om nul te zijn.

[TOC]

Hoe de bepalingscoëfficiënt te berekenen?

In de vorige paragraaf werd gezegd dat de bepalingscoëfficiënt wordt berekend door het quotiënt tussen de varianties te vinden:

-Geschat door de regressiefunctie van de variabele en 

-De Yi -variabele die overeenkomt met elk van de XI -variabele. 

In wiskundige vorm blijft het als volgt:

R² = Sŷ / SY

Uit deze formule volgt dat r² vertegenwoordigt het deel van de variantie verklaard door het regressiemodel. Als alternatief kan r worden berekend² Door de volgende formule, volledig gelijk aan de vorige:

R² = 1 - (sε / sy)

Waarbij Sε de variantie van het afval vertegenwoordigt εi = ŷi - yi, terwijl SY de variantie is van de gegevensset van de gegevens van de gegevens. Om te bepalen ŷi wordt de regressiefunctie toegepast, wat betekent dat ŷi = f (xi) bevestigt.

Het kan u van dienst zijn: fractie gelijk aan 3/5 (oplossing en uitleg)

De variantie van de YI -gegevensset, met i van 1 tot n wordt op deze manier berekend:

Sy = [σ (yi -)² ) / (N-1)]

En ga dan op een vergelijkbare manier door voor Sŷ of voor Sε.

Illustratief geval

Door de details te tonen van de manier waarop de berekening van de Vastberadencoëfficiënt We zullen de volgende set van vier paar gegevens nemen: 

(X, y): (1, 1); (23); (3, 6) en (4, 7).

Een lineaire regressie -aanpassing wordt voorgesteld voor deze gegevensset verkregen door de methode van de vierkante minima:

f (x) = 2.1 x - 1 

Door deze aanpassingsfunctie toe te passen, worden de collega's verkregen:

(X, ŷ): (1, 1.1); (23.2); (3, 5.3) en (4, 7.4).

Vervolgens berekenen we het rekenkundige gemiddelde voor X en Y:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Variantie SY

Sy = [(1 - 4.25)² + (3. 4.25)² + (6 - 4.25)² +.. ... .(7 - 4.25)²] / (4-1) =

= [-3.25)²+ (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.583

Variantie Sŷ

Sŷ = [(1.1 - 4.25)² + (3.2 - 4.25)² + (5.3. 4.25)² +.. ... .(7.4 - 4.25)²] / (4-1) =

= [-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (3)] = 7.35

Bepalingscoëfficiënt r²

R² = Sŷ / sy = 7.35/7.58 = 0.97

Interpretatie

De bepalingscoëfficiënt voor het illustratieve geval dat in het vorige segment wordt beschouwd, bleek 0 te zijn.98. Dat wil zeggen dat de lineaire aanpassing door de functie:

 f (x) = 2.1x - 1

Het is 98% betrouwbaar om de gegevens te verklaren waarmee deze is verkregen via de minimale vierkante methode. 

Naast de bepalingscoëfficiënt is er de Lineaire correlatiecoëfficiënt of ook bekend als Pearson -coëfficiënt. Deze coëfficiënt, aangeduid als R, Het wordt berekend door de volgende relatie:

R = sxy / (sx sy)

Hier vertegenwoordigt de teller de covariantie tussen de variabelen X en Y, terwijl de noemer het product is van de standaardafwijking voor variabele X en de standaardafwijking voor de variabele en.

De coëfficiënt van Pearson kan waarden aannemen tussen -1 en +1. Wanneer deze coëfficiënt neigt naar +1, is er directe lineaire correlatie tussen X en Y. Als het in plaats daarvan neigt naar -1, is er lineaire correlatie, maar wanneer X groeit en afneemt. Ten slotte is het bijna 0, er is geen verband tussen de twee variabelen.

Kan u van dienst zijn: Gegroepeerde gegevens: voorbeelden en oefening opgelost

Opgemerkt moet worden dat de bepalingscoëfficiënt samenvalt met het kwadraat van de Pearson -coëfficiënt, alleen wanneer de eerste is berekend op basis van een lineaire aanpassing, maar deze gelijkheid is niet geldig voor andere niet -lineaire aanpassingen.

Voorbeelden

- voorbeeld 1

Een groep middelbare scholieren is van plan een empirische wet te bepalen voor de periode van een slinger als functie van de lengte. Om dit doel te bereiken, doen ze een reeks metingen waarin ze de tijd van een slinger oscillatie meten voor verschillende lengtes die de volgende waarden verkrijgen:

Lengte (m)	Periode (s)
0,1	0,6
0,4	1.31
0,7	1.78
1	1.93
1.3	2.19
1.6	2.66
1.9	2.77
3	3.62

Er wordt gevraagd om een ​​gegevensdispersgrafiek te maken en een lineaire aanpassing te maken door regressie. Toon bovendien de regressievergelijking en de bepalingscoëfficiënt ervan.

Oplossing

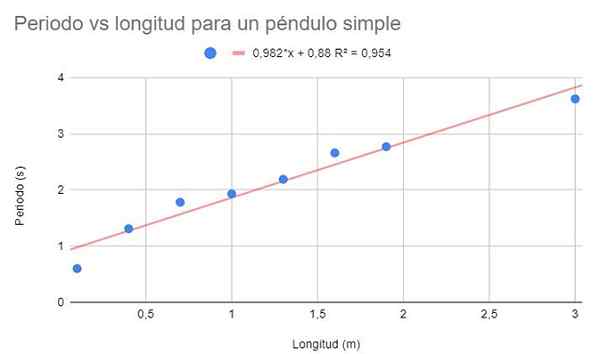Figuur 2. Grafische oplossing van oefening 1. Bron: f. Zapata.

Een vrij hoge bepalingcoëfficiënt (95%) kan worden waargenomen, dus men kan worden gedacht dat de lineaire aanpassing optimaal is. Als de punten echter samen worden waargenomen, lijkt het erop dat ze de neiging hebben om te buigen. Dit detail wordt niet overwogen in het lineaire model.

- Voorbeeld 2

Voor dezelfde gegevens van voorbeeld 1, maak een gegevensdispersietabel. Bij deze gelegenheid wordt, in tegenstelling tot voorbeeld 1, gevraagd om een ​​regressie -aanpassing te maken via een potentiële functie.

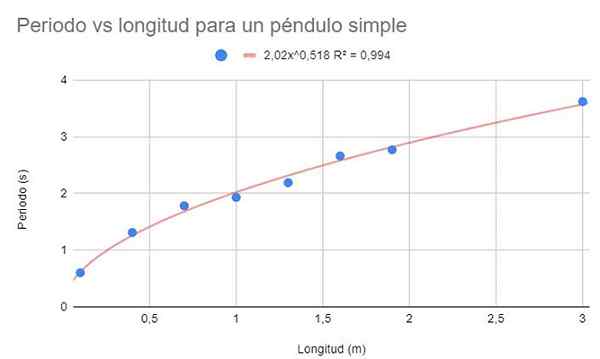figuur 3. Grafische oplossing van oefening 2. Bron: f. Zapata.

Toon ook de aanpassingsfunctie en de R -bepalende coëfficiënt².

Oplossing

De potentiële functie is van de vorm f (x) = ax^B, waarbij a en b constant zijn die worden bepaald door een minimale vierkante methode.

De vorige figuur toont de potentiële functie en de parameters ervan, evenals de bepalingscoëfficiënt met een zeer hoge waarde van 99%. Merk op dat de gegevens de kromming van de trendlijn volgen.

Kan u van dienst zijn: additief principe

- Voorbeeld 3

Met dezelfde gegevens van voorbeeld 1 en voorbeeld 2, maak een tweede -graafpolynoomaanpassing. Toon de grafiek, de aanpassingspolynoom en de bepalingcoëfficiënt r² correspondent.

Oplossing

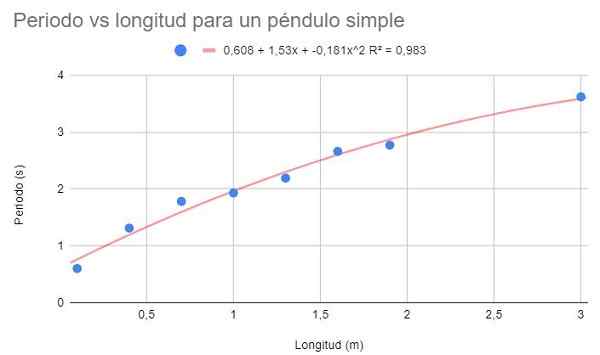Figuur 4. Grafische oefening 3 grafiek. Bron: f. Zapata.

Met de tweede graad polynoomaanpassing is een trendlijn te zien die goed past bij de kromming van de gegevens. Evenzo ligt de bepalingscoëfficiënt boven de lineaire aanpassing en onder de potentiële aanpassing.

Aanpassingsvergelijking

Van de drie getoonde aanpassingen is die met een hogere bepalingcoëfficiënt de potentiële aanpassing (Voorbeeld 2).

De potentiële aanpassing valt samen met de fysieke theorie van de slinger, die, zoals bekend, vaststelt dat de periode van een slinger evenredig is met de vierkantswortel van zijn lengte, de constante van evenredigheid 2π /√g waarbij G de versnelling is van de zwaartekracht.

Dit type potentiële aanpassing heeft niet alleen de hoogste bepalingscoëfficiënt, maar de exponent- en evenredigheidsconstante valt samen met het fysieke model. 

Conclusies

-De regressie -aanpassing bepaalt de parameters van de functie die tot doel heeft de gegevens te verklaren via de minimale vierkante methode. Deze methode bestaat uit het minimaliseren van de som van het kwadratische verschil tussen de waarde en aanpassing en de YI -waarde van de gegevens voor de XI -waarden van de gegevens. Op deze manier worden de parameters van de aanpassingsfunctie bepaald.

-Zoals we hebben gezien, is de meest voorkomende aanpassingsfunctie de lijn, maar het is niet de enige, omdat de aanpassingen ook polynoom, potentiële, exponentiële, logaritmen en andere kunnen zijn. 

-In elk geval is de bepalingscoëfficiënt afhankelijk van de gegevens en het type aanpassing en is een indicatie van de goedheid van de toegepaste aanpassing.

-Ten slotte geeft de bepalingscoëfficiënt het percentage van de totale variabiliteit tussen de waarde en de gegevens aan met betrekking tot de ŷ -waarde van de aanpassing voor de X gegeven.

Referenties

1. González C. Algemene statistieken. Hersteld van: tarwi.La Molina.Edu.pe
2. IACS. Aragonese Institute of Health Sciences. Opgehaald uit: ICS-Aragon.com
3. Salazar C. en Castillo S. Basisstatistiekenprincipes. (2018). Opgehaald uit: DSPACE.Uce.Edu.EC
4. Superprof. Vastberadencoëfficiënt. Hersteld van: superprof.is
5. USAC. Beschrijvende statistiekenhandleiding. (2011). Hersteld van: statistieken.engineering.USAC.Edu.GT.
6. Wikipedia. Vastberadencoëfficiënt. Hersteld van: is.Wikipedia.com.