Orthogonale matrixeigenschappen, demonstratie, voorbeelden

Jij hebt er een Orthogonale matrix Wanneer genoemde matrix vermenigvuldigd met zijn transponeringsresultaten in de identiteitsmatrix. Als de inverse van een matrix gelijk is aan de getransponeerde, is de oorspronkelijke matrix orthogonaal.

Orthogonale matrices zijn kenmerkend dat het aantal rijen gelijk is aan het aantal kolommen. Bovendien zijn rijvectoren eenheid orthogonale vectoren en zijn de uitslag van getransponeerde vectoren dat ook.

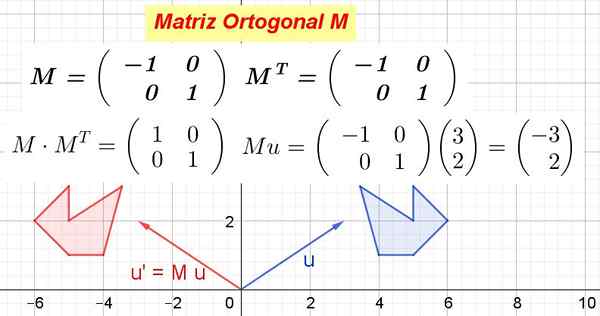Figuur 1. Voorbeeld van orthogonale matrix en hoe geometrische objecten transformeert. (Opgesteld door Ricardo Pérez)

Wanneer een orthogonale matrix wordt vermenigvuldigd met de vectoren van een vectorruimte, produceert isometrische transformatie, dat wil zeggen een transformatie die de afstanden niet verandert en de hoeken behoudt.

Een typische vertegenwoordiger van orthogonale matrices zijn de rotatiematrices. De transformaties van orthogonale matrices op een vectorruimte worden genoemd Orthogonale transformaties.

De geometrische transformaties van rotatie en reflectie van punten die worden weergegeven door zijn Cartesiaanse vectoren worden gemaakt door orthogonale matrices op de oorspronkelijke vectoren toe te passen om de coördinaten van de getransformeerde vectoren te verkrijgen. Het is om deze reden dat orthogonale matrices op grote schaal worden gebruikt bij de grafische verwerking van computers.

[TOC]

Eigenschappen

Een reeks M Het is orthogonaal als het wordt vermenigvuldigd door zijn transponering M^T De identiteitsmatrix resulteert in Je. Evenzo is het product van het transponeren van een orthogonale matrix door de oorspronkelijke matrix van de identiteitsmatrix:

M m^T = M^T M = i

Als gevolg van de vorige verklaring is de getransponeerde van een orthogonale matrix gelijk aan de inverse matrix:

M^T = M^-1.

De set van orthogonale dimensiematrices n x n Ze vormen de orthogonale groep Of (n). En de subset van Of (n) van orthogonale matrices met het bepalen van +1 vormen de Special Matrices Group ITS (n). Matrices van de groep Uw (n) Het zijn matrices die lineaire rotatietransformaties produceren, ook bekend als de Rotaties groep.

Demonstratie

We zullen aantonen dat een matrix orthogonaal is als en alleen als de rijvectoren (of kolomvectoren) orthogonaal voor elkaar zijn en van norm 1.

Kan u van dienst zijn: Bayes Stelling

Neem aan dat de gelederen van een orthogonale matrix n x n n ortonormale vectoren van dimensie n zijn. Als het wordt aangegeven door v1, v2,.. ., vN De N -vectoren zijn vervuld:

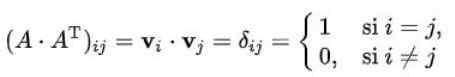
Waar het duidelijk is dat de set rijvectoren een set orthogonale vectoren is met norm één.

Voorbeelden

voorbeeld 1

Laat zien dat de 2 x 2 matrix die de vector op de eerste rij heeft V1= (-1 0) en in de tweede rij de vector V2= (0 1) is een orthogonale matrix.

Oplossing: De matrix is ​​gebouwd M en het transponeren wordt berekend M^T:

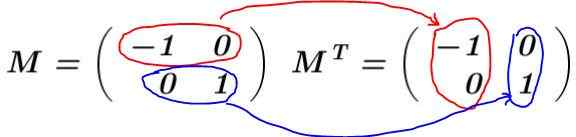
In dit voorbeeld, de matrix M Het is een getransponeerde auto, dat wil zeggen dat de matrix en zijn transponeren identiek zijn. Het vermenigvuldigt M voor zijn transponering M^T:

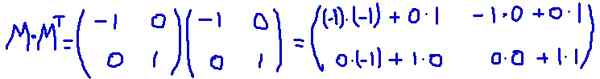
Het is dat geverifieerd M M^T Het is gelijk aan de identiteitsmatrix:

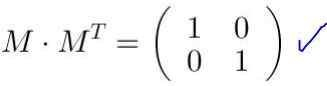
Wanneer de matrix M Het wordt vermenigvuldigd met de coördinaten van een vector of een punt, nieuwe coördinaten worden verkregen die overeenkomen met de transformatie die de matrix op de vector of het punt maakt.

Figuur 1 laat zien hoe M Transformeert de vector of in of' En ook zoals M Transformeer de blauwe polygoon in de rode polygoon. Als M Het is orthogonaal, het is dan een orthogonale transformatie, die afstanden en hoeken behoudt.

Voorbeeld 2

Stel dat u een 2 x 2 -matrix hebt gedefinieerd in de REAI's gegeven door de volgende uitdrukking:

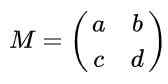
Vind de echte waarden van naar, B, C En D zodat de matrix M Wees een orthogonale matrix.

Oplossing: Per definitie is een matrix orthogonaal als ze worden vermenigvuldigd met zijn transponering wordt verkregen als gevolg van de identiteitsmatrix. Herinnerend dat de getransponeerde matrix wordt verkregen uit de originele, uitwisselende rijen door kolommen is de volgende gelijkheid:

Het kan u van dienst zijn: domein en tegenspraak met een functie (met voorbeelden)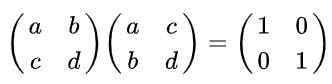

Het uitvoeren van de matrixvermenigvuldiging is:

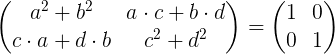
Gelijk aan de elementen van de linkermatrix met de elementen van de identiteitsmatrix aan de rechterkant, verkrijgen we een systeem van vier vergelijkingen met vier onbekenden A, B, C en D.

We stellen voor A, B, C en D de volgende uitdrukkingen voor op basis van trigonometrische redenen sinus en cosinus:

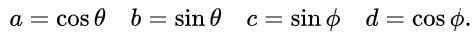
Met dit voorstel en vanwege de fundamentele trigonometrische identiteit, wordt de eerste en derde vergelijking in de gelijkheid van de matrixelementen automatisch voldaan. De derde en vierde vergelijking zijn hetzelfde en in matrix gelijkheid na het vervangen van de voorgestelde waarden is als volgt:

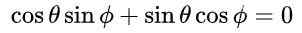
wat leidt tot de volgende oplossing:

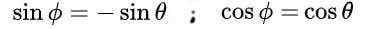
Ten slotte worden de volgende oplossingen verkregen voor de orthogonale matrix M:

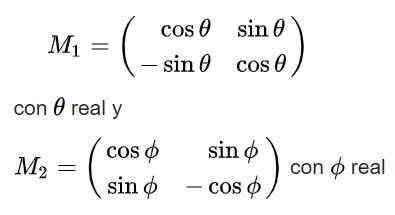
Merk op dat de eerste van de oplossingen een bepalende factor +1 heeft, dus het behoort tot de ITS -groep (2), terwijl de tweede oplossing een determinant -1 heeft en daarom niet tot deze groep behoort.

Voorbeeld 3

Gezien de volgende matrix, zoek de waarden van A en B om een ​​orthogonale matrix te hebben.

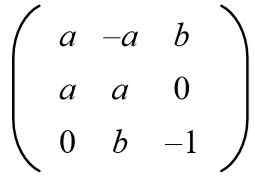
Oplossing: Voor een bepaalde matrix die orthogonaal is, moet het product met zijn transponering de identiteitsmatrix zijn. Vervolgens wordt het matrixproduct van de matrix gegeven met de getransponeerde matrix gemaakt met het volgende resultaat:

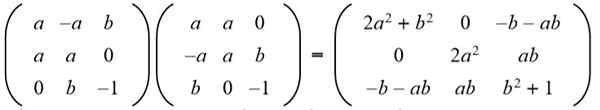
Vervolgens wordt het resultaat gekoppeld aan de identiteitsmatrix 3 x 3:

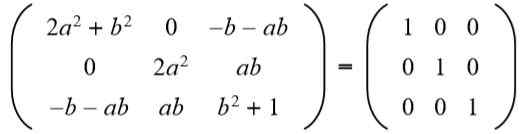
In de tweede rij derde kolom heb je (A B = 0), Maar naar Het kan niet nul zijn, want als dat zo is, zou de gelijkheid van de elementen van de tweede rij en de tweede kolom niet worden vervuld. Dan noodzakelijkerwijs B = 0. Vervangend B Voor de waarde 0 hebben we:

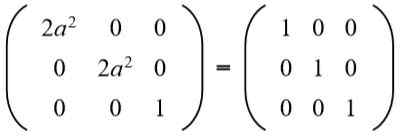
Dan wordt de vergelijking opgelost: 2a^2 = 1, Wiens oplossingen zijn: +½√2 en -½√2.

Kan u van dienst zijn: soorten hoeken, kenmerken en voorbeelden

De positieve oplossing nemen naar naar Het resulteert in de volgende orthogonale matrix:

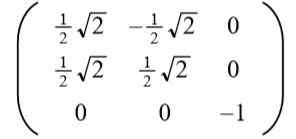
De lezer kan gemakkelijk verifiëren dat de rijenvectoren (en ook kolomvectoren) orthogonaal en eenheid zijn, dat wil zeggen ortonormaal.

Voorbeeld 4

Toon aan dat de matrix NAAR wiens rijen zijn V1 = (0, -1 0), V2 = (1, 0, 0) En V3 = (0 0 -1) Het is een orthogonale matrix. Zoek bovendien hoe de vectoren van de canonieke basis worden getransformeerd I J K Aan de vectoren U1, U2 En U3.

Oplossing: Er moet aan worden herinnerd dat het element (i, j) van een matrix vermenigvuldigd met zijn transponering, het scalaire product is van de vector van rij (i) door de kolom (j) van de transponering. Bovendien is dit product gelijk aan de delta van Kronecker voor het geval de matrix orthogonaal is:

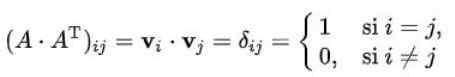
In ons geval is het zo:

V1 • v1 = 0x0 + (-1) x (-1) + 0x0 = 1

V2 • v2 = 1 × 1 + 0x0 + 0x0 = 1

V3 • v3 = 0x0 + 0x0 + (-1) x (-1) = 1

V1 • v2 = 0x1 + (-1) x0 + 0x0 = 0

V2 • v1 = 1 × 0 + 0x (-1) + 0x0 = 0

V2 • v3 = 1 × 0 + 0x (0) + 0x (-1) = 0

V3 • v2 = 0x1 + 0x (0) + (-1) x0 = 0

V1 • v3 = 0x0 + (-1) x (0) + 0x (-1) = 0

V3 • v1 = 0x0 + 0x (-1) + (-1) x0 = 0

Met wat wordt aangetoond dat het een orthogonale matrix is.

Daarnaast u1 = a i = (0, 1, 0); U2 = a j = (-1, 0, 0) en ten slotte U3 = a k = (0, 0, -1)

Referenties

1. Anthony Nicolaides (1994) Determinanten en matrices. Pass Publicatie.
2. Birkhoff en Maclane. (1980). Modern Algebra, ed. Vicens-Vives, Madrid.
3. Casteleiro Villalba M.  (2004) Inleiding tot lineaire algebra. ESIC -redactie.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
6. Richard J. Brown (2012) 30-seconden wiskunde: de 50 meest geestverruimende theorieën in wiskunde. Ivy Press Limited.
7. Wikipedia. Orthogonale matrix. Hersteld van: is.Wikipedia.com
8. Wikipedia. Orthogonale matrix. Opgehaald uit: in.Wikipedia.com