Biot-Savart Law-formule, demonstratie, toepassingen, oefeningen

De Biot-Savart Law vestigt een relatie tussen het magnetische veld DB  Op een punt P, geproduceerd door een dunne draad die een stroom I transporteert en wiens differentiële lengte is DS. Deze wet wordt gebruikt om het magnetische veld van huidige distributies te vinden via de Superpositieprincipe. 

Dit betekent dat om het totale magnetische veld op punt P te berekenen, we alle bijdragen moeten toevoegen dat elk differentiaal deel DS van de draad draagt ​​bij. En deze som wordt gedaan door een integrale uitgevoerd over de gehele huidige verdeling.

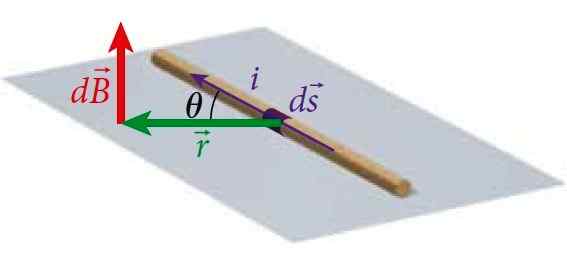
Figuur 1. Een draadsegment transporteert een stroom I, die een magnetisch veld produceert op een punt P op een bepaalde afstand van de draad, die wordt berekend door de biot-savartwet. Bron: Bauer, W. Fysica voor engineering en wetenschappen.

Op deze manier kunt u het veld berekenen dat draden produceert met stroom van verschillende geometrieën.

De wet van Biot-Savart is vernoemd naar de twee Franse fysici die het in 1820 ontdekten: Jean Marie Biot (1774-1862) en Felix Savart (1791-1841). Om dit te bereiken, moesten ze de intensiteit en vorm bestuderen van het magnetische veld dat werd geproduceerd door talloze huidige distributies.

[TOC]

Formule

De wiskundige uitdrukking van de biot-savartwet is als volgt:

Het handhaaft analogieën met zijn equivalent om het elektrische veld te berekenen: de wet van Coulomb, alleen dat het magnetische veld DB in p is loodrecht naar het vlak waar de draad zich bevindt. We kunnen dit zien in figuur 1.

De vorige uitdrukking kan ook als volgt worden geschreven:

In beide uitdrukkingen, R Het is de positievector, gericht op het ID -stroomelementS tot het punt waarop u het veld wilt berekenen.

Kan u van dienst zijn: behoud van het lineaire momentum: principe, voorbeelden, oefeningen.

Voor zijn deel, R Met een circumflejo -accent is het de unitaire vector die in dezelfde richting en richting wordt gericht, maar met een module gelijk aan 1. De vector R Het wordt als volgt weergegeven:

Om deze reden, door in de vorige vergelijking te vervangen -de die r³ In de noemer- de uitdrukking R wordt onmiddellijk bereikt² In de noemer.

Naast de bovengenoemde vectoren bevat de formule de constante μ_of, telefoongesprek Vacuümpermeabiliteit en Wiens waarde is:

μ_of = 4π x10^-7 T.m/ a.

Als we de magnetische veldvector willen berekenen, is het noodzakelijk om alle huidige verdeling te integreren, waarvoor we de gegevens over de geometrie nodig hebben:

Het vectorproduct en de rechterhandregel

De biot-savartwet omvat een vectorproduct tussen ID-vectorenS En R. Het resultaat van een vectorproduct tussen twee vectoren is ook een vector.

In dit geval de ID -vectorproductmoduleS X R is: (ids) ⋅r⋅senθ, waarbij θ de hoek is tussen IDS En R, Zoals getoond in figuur 1.

Op deze manier de omvang van het veld DB Het wordt gegeven door:

De richting en betekenis kunnen worden bepaald met de regel van de rechterhand, die in deze figuur wordt geïllustreerd:

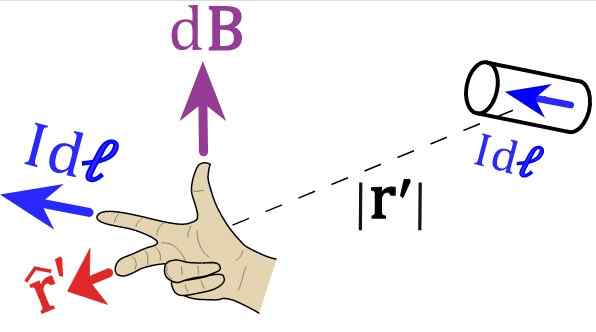Figuur 2. Rechtsregel voor biot-savartwet. Bron: Wikimedia Commons.

We nodigen de lezer uit om zijn rechterhand te positioneren volgens de vectoren van figuren 1 en 2. Voor figuur 1 moet de wijsvinger naar links wijzen, na IDS of idl, De middelvinger wijst volgens de vector R eenheid.

En ten slotte wordt de duim gericht en dit is de richting van het magnetische veld.

Kan u van dienst zijn: ellipsoïde: kenmerken en voorbeelden

Demonstratie van de biot-savartwet

De biot-savartwet is bij uitstek experimenteel, wat betekent dat de formulering ervan voortkomt uit vele observaties over het gedrag van het magnetische veld dat wordt geproduceerd door huidige draden.

Biot- en Savart -observaties

Dit waren de observaties van Franse wetenschappers over het magnetische veld DB:

-De omvang van DB is omgekeerd evenredig met R².

-Het is ook recht evenredig met de grootte van het huidige element, dat ID wordt genoemdS En ook voor sen θ, waarbij θ de hoek is tussen de vectoren DS En R.

-DB staat loodrecht op beide IDS -de richting van de huidige R.

-Divers van dB is tangentieel voor een radiocirkel R draadgericht. Met andere woorden, veld B geproduceerd door een huidige segment bestaat uit concentrische omtrek naar de kale.

-De betekenis waarin het draait B Het wordt gegeven door de rechter duimregel: de rechterduim wordt gericht op de richting van de stroom en de resterende vier vingers zijn gekruld rond de draad, na de circulatie van het veld.

Al deze observaties worden gecombineerd in de wiskundige uitdrukking van de eerder beschreven wet.

Biot-Savart Law-aanvragen

Wanneer de huidige verdeling hoge symmetrie heeft, kan integrale eenvoudig worden opgelost, laten we enkele gevallen bekijken:

Rechtlijnige en dunne draad

Een rechtlijnige draad van lengte L transporteert een stroom I, zoals die in de figuur.

Het illustreert de benodigde geometrie voor de berekening van het veld. Dit staat loodrecht op het vel papier, extravert naar het vlak als de stroom van links naar rechts stroomt en anders inkomen (controleer het met de rechterhandregel).

Kan u van dienst zijn: paramagnetisme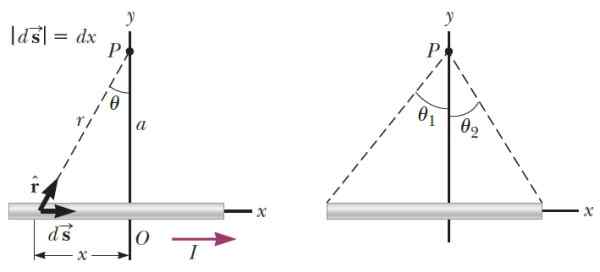figuur 3.- Aan de linkerkant is de geometrie die nodig is om het magnetische veld te berekenen dat een dun draadsegment produceert op punt P. Rechts de hoeken die de positie van P bepalen ten opzichte van de uiteinden van het segment. Bron: Serway, r. Natuurkunde voor wetenschap en engineering.

Zijn k  De eenheidsvector in de richting loodrecht op het vlak, na het uitvoeren van het integratieproces, is het magnetische veld dat de draad produceert in P:

Circulaire spira

De radiocirculaire lus naar Het transporteert een stroom zoals weergegeven in de figuur en produceert een magnetisch veld DB -in donkergroen- op punt P op de axiale as, op een afstand X Vanuit het midden.

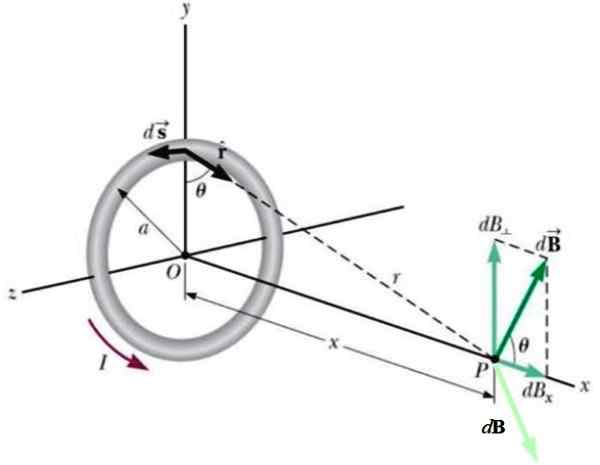Figuur 4.- Geometrie voor de berekening van het veld geproduceerd door de cirkelvormige spase op punt P op de axiale as. Bron: Wikimedia Commons.

Een ander stroomelement aan de andere kant zou een nieuwe bijdrage leveren aan de DB (lichtgroen), zodat de verticale component wordt geannuleerd met de eerste.

Het resultaat is dat het netto magnetische veld horizontaal is, dus het is alleen geïntegreerd in deze componenten, wat resulteert in:

Oefening opgelost

Er is een extreem lange draad die een stroom van 2 transporteert om te stromen zoals weergegeven in het beeld. Bereken de grootte van het magnetische veld op een radiale afstand van 5 cm van de draad.

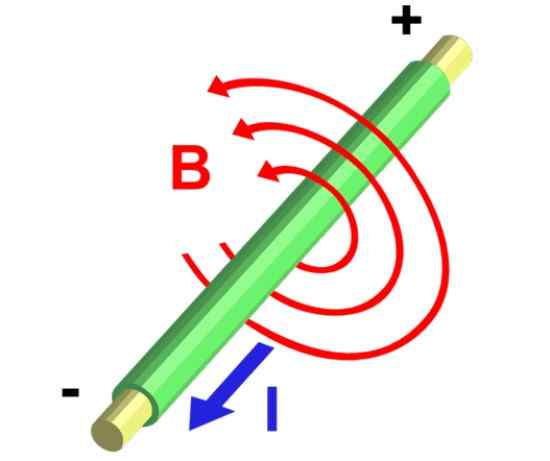Figuur 5.- Magnetische veldlijnen van een rechtlijnig draadsegment dat stroom transporteert. Bron: Wikimedia Commons.

Oplossing

Omdat het een zeer lange draad is, kunnen we de uitdrukking nemen voor het rechtlijnige segment en θ maken₁= 0º en θ₂ = 180º voor limiethoeken. Dit is voldoende voor de lengte van de draad om oneindig op te slaan.

Op deze manier zullen we het veld hebben is:

Dat vereenvoudigt:

Nu vervangen we de waarden van de verklaring:

I = 2 a

R = 5 x10^-2 M

μ_of= 4π x10^-7 T.m/ a

De richting en het gevoel van B Ze worden getoond in figuur 5, waar de richting die het vel verlaat, is genomen als k.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Deel 6. Elektromagnetisme. Uitgegeven door Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
4. Resnick, r. 199999. Fysiek. Vol. 1. 3e ed. in het Spaans. Continental Editorial Company s.NAAR. van C.V.
5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1.
6. Serway, r., Jewett, J. 2008. Natuurkunde voor wetenschap en engineering. Deel 2. 7e. ED. Cengage leren.