Trigonometrische identiteiten (voorbeelden en oefeningen)

De trigonometrische identiteiten Dit zijn relaties tussen trigonometrische redenen, die waar zijn voor elke waarde van de variabele. Bijvoorbeeld:

Tan θ = sin θ /cos θ

Het is een trigonometrische identiteit die drie redenen van de hoek θ, de raaklijn, de borst en de cosinus van genoemde hoek relateert.

Figuur 1. Sommige trigonometrische identiteiten die veel worden gebruikt in de berekening. Bron: f. Zapata.

Deze identiteit is waar voor alle waarde, behalve die welke 0 de noemer maken. De cos θ is 0 voor θ = ± π/2, ± 3π/2, ± 5π/2 ... Een ander voorbeeld van trigonometrische identiteit is:

Sin x . SEC X . CTG X = 1

[TOC]

Demonstratie

Er zijn twee basis manieren om aan te tonen dat een trigonometrische identiteit waar is:

1- Een van de leden van gelijkheid transformeren in de andere, door handige algebraïsche manipulaties.

2- Ontwikkel beide leden van gelijkheid afzonderlijk, totdat de respectieve uiteindelijke uitdrukkingen van elk exact hetzelfde zijn.

In de voorgestelde identiteit gaan we de linkerkant van gelijkheid transformeren, waarvoor we CTG X en SEC X uitdrukken in termen van borst en cosinus als volgt:

Ctg x = cos x / sen x

Sec x = 1 /cos x

We vervangen deze uitdrukking aan de linkerkant van identiteit en vereenvoudigen:

Sin x . (1/cos x). (cos x / sen x) = (sin x. cos x / cos x . sin x) = 1

En de waarheidsgetrouwheid van identiteit is al bewezen.

Soorten trigonometrische identiteiten

Er zijn verschillende soorten trigonometrische identiteiten. Vervolgens zullen we kort de belangrijkste beschrijven:

- Fundamentele trigonometrische identiteiten

We onderscheiden twee soorten fundamentele identiteiten:

I) Degenen die worden uitgedrukt door de basisredenen, cosinus en raaklijn:

• Sec x = 1 /cos x
• Schade x / 1 / sin x
• Ctg x = 1 / tg x
• Tg x = sin x /cos x
• Ctg x = cos x / sen x

I) die afgeleid van pariteit. We weten door de grafiek dat Sen X een vreemde functie is, wat betekent dat:

Kan u van dienst zijn: 60 delers

sin (-x) = - sin x

Van zijn deel is cos x daarom een ​​paar:

cos (-x) = cos x

Dus:

tg (-x) = sen (-x) / cos (-x) = -sen x / cos x

Op dezelfde manier:

• cotg (-x) = -ctg x
• sec (-x) = sec x
• harm (-x) = - schade x

- Pythagorische identiteiten

Zij zijn degenen verkregen uit de toepassing van de Pythagoras -stelling op de rechthoekige driehoek van katten A en B en Hypotenusa C. Laten we eens kijken:

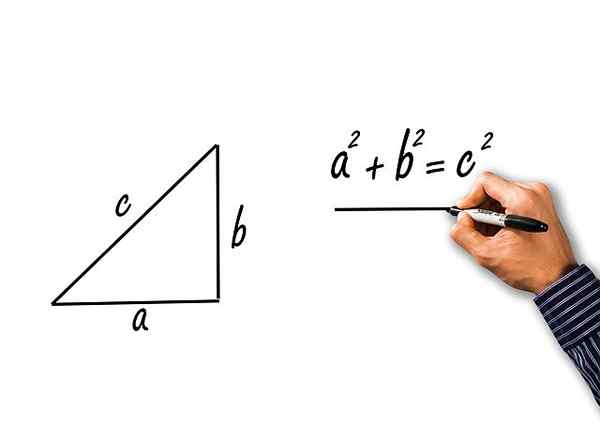Figuur 2.- Uit Pythagoras Stelling worden de drie Pythagorese trigonometrische identiteiten verkregen. Bron: Pixabay.

De stelling van Pythagoras stelt dat:

C² = A² + B²

Alles verdelen tussen c²:

C² / C² = (a² / C²) + (B² / C²))

De term aan de linkerkant is 1 en onthouden dat de sinus en cosinus van de acute hoek α worden gedefinieerd als:

sin α = a/c

cos α = b/c

Resultaat:

1 = (sin α)² + (cos α)²

Deze identiteit staat bekend als Fundamentele identiteit.

De procedure kan worden uitgevoerd door te delen tussen² en B², die aanleiding geeft tot nog twee identiteiten:

Second² α = 1 + tg² α

har² α = 1 + CTG² α

- Formules voor cosinus en de borst van de som/aftrekking van hoeken

De belangrijkste trigonometrische identiteiten voor cosinus, borst en raaklijn van de som en aftrekking zijn de volgende:

SEN -demonstratie (α + β) en COS (α + β)

Deze identiteiten kunnen geometrisch worden aangetoond of ook via de Euler -formule:

En^Iα = cos α + i sin α

Laten we eens kijken wat er met de formule gebeurt bij het vervangen van de som van twee hoeken α en β:

En^{Ik (α +β))} = cos (α + β) + i sin (α + β)

Deze expressie is complex, het reële deel is cos (α + β) en het denkbeeldige deel is I sin (α + β). We houden dit resultaat om het later te gebruiken en ons te concentreren op het ontwikkelen van het exponentiële deel:

En^{Ik (α +β))} = e^Iα ⋅ e^Ip = (cos α + i sin α) . (cos β + i sin β) =

Kan je van dienst zijn: zeshoekige prisma

= cos α⋅cos β + cos α⋅i sen β + i⋅sen α cos β - sen α⋅sen β

Het echte deel van deze uitdrukking is degene die niet wordt vermenigvuldigd door de denkbeeldige eenheid "I":

cos α⋅cos β - sen α. Sen β

Het denkbeeldige deel is daarom:

I (cos α⋅sen β + sen α⋅cos β)

Om twee complexe uitdrukkingen hetzelfde te zijn, moet het echte deel van de ene gelijk zijn aan het echte deel van de andere. Hetzelfde geldt voor denkbeeldige delen.

We nemen de opgeslagen uitkomst en vergelijk het hiermee:

Cos α. cos β - sen α. sin β = cos (α + β)

I (cos α⋅sen β + sen α⋅cos β) = i sin (α + β)

sin (α + β) = (cos α. sin β + sen α⋅cos β)

- Formules voor de dubbele hoek

In de vorige formules nemen we β = α en ontwikkelen we:

sin (α + α) = sen 2 α = sen α⋅cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - sen α⋅sen α = cos² α - Sen ² α

Tg (α + α) = Tg 2 α = [Tg α + Tg α] / [1- Tg α⋅TG α] = 2tg α / 1- tg² α

Als in de tweede uitdrukking wordt vervangen² α = 1 - sen² α wordt verkregen:

cos 2 α = cos² α- (1- COS² α) = 2 cos² α -1

- Half -hoek -formules

In deze laatste uitdrukking vervangen we α door α/2, de volgende overblijfselen:

cos α = 2 cos ²(α/2) -1

Opruimen:

Opgeloste oefeningen

- Oefening 1

Laat zien:

Oplossing

We gaan algebraïschal de term links werken, zodat deze eruit ziet als rechts. Zoals in de juiste termijn verschijnt sen x, is de eerste stap om cos uit te drukken²X In termen van Sen X zodat alles in termen van dezelfde trigonometrische reden is:

Het kan u van dienst zijn: fractie gelijk aan 3/5 (oplossing en uitleg)

Dan is 1 - Sen is factor² x voor een verschil met perfecte vierkanten. Om dit te doen verdwijnt het van de fundamentele identiteit:

zomaar²X = 1 - Sen² X

1 - Sen² x = (1- sin x) (1+senx)

En de factorisatie in de oorspronkelijke uitdrukking wordt vervangen:

De term (1- senx) is vereenvoudigd en er blijft een gelijkheid bestaan:

1 + sen x = 1 + senx

- Oefening 2

Los de volgende trigonometrische vergelijking op en geef de oplossing voor waarden tussen 0 en 360º:

TG X + SEC² X = 3

Oplossing

In de looptijd van links zijn er twee trigonometrische redenen, daarom moet u alles terugbrengen tot één, om het onbekende te kunnen wissen. De term sec² X wordt uitgedrukt door een van de Pythagoras -identiteiten:

Second² α = 1 + tg² α

Door de vergelijking te vervangen:

TG X + 1 + TG² X = 3

De voorwaarden herschikken:

TG² x + tg x + 1 = 3

Deze vergelijking wordt opgelost door de variabele te wijzigen:

tg x = u

of² + U + 1 - 3 = 0 → U² + U - 2 = 0

Deze tweede graadvergelijking kan gemakkelijk worden opgelost door factorisatie:

(U +2) (u-1) = 0

Daarom u₁ = -2 en u₂ = 1, equivalent aan:

TG X₁ = -2

TG X₂ = 1

Eindelijk:

X₁ = arctg (-2) = 296.6e

X₂  = arctg (1) = 45º

Referenties

1. Carena, m. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Presiversity wiskundehandleiding. Nationale Universiteit van de kust.
2. Figuera, j. 199999. Wiskunde. 1e. Diversifieerd. Bolivarian collegiale edities.
3. Hoffman, J. Selectie van wiskundeproblemen. Deel 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Wikipedia. Trigonometrie -identiteiten en formules. Hersteld van: is.Wikipedia.borg.
6. Zapata, f. 4 manieren om een ​​tweede graad vergelijking op te lossen. Hersteld van: Francesphysics.Blogspot.com.
7. Zill, D. 1984. Algebra en trigonometrie. McGraw Hill.