Geschiedenis van de achtergrond- en ontwikkelingsgeometrie van zijn oorsprong

De Geometriegeschiedenis Het begint met de eerste beschavingen die op een praktische manier gebruik maakten van deze tak van wiskunde, met name de volkeren van de Indo -vallei en Babylon die de stompe driehoeken kenden, ongeveer 3000.C.

In de geschriften van de Egyptische schrijver Ahmes (1550 tot.C.) Methoden worden gebruikt om het gebied van een cirkel te berekenen. Van hun kant hadden de Babyloniërs algemene regels om delen en gebieden te meten. 

Ahme papyrus of rhind wiskundige papyrus

Beide beschavingen, de Egyptenaren en Babyloniërs, kenden versies van de Pythagoras Stelling 1500 jaar vóór de Pythagorische versies. Aan de andere kant, de Indianen van de Vedische periode (1500-100 tot.C.) gebruikte geometrie in altarenconstructie.

[TOC]

Het oude Griekenland

De Grieken waren lange tijd geneigd naar de ontwikkeling van wiskunde. Personages zoals Pythagoras en Plato, gerelateerd aan cijfers met alles wat in de wereld bestaat. Voor hen was wiskunde de sleutel tot het interpreteren van het universum; Dit ideaal volgde al enkele eeuwen in de volgers van Pythagoreeërs.

Verhalen over Miletus

Tales de Mileto was een van de eerste Grieken die bijdroeg aan de vooruitgang van geometrie. Een lange tijd doorgebracht in Egypte en van deze geleerde basiskennis. Hij was de eerste die geometriemeetformules vaststelde.

Verhalen over Miletus

Hij slaagde erin om de hoogte van de piramides van Egypte te meten, waarbij hij zijn schaduw meten op het exacte moment waarop de hoogte gelijk was aan de maat van zijn schaduw.

Pythagoras

Pythagoras

Binnen de belangrijkste bijdrage van Pythagoras (569 tot.C. - 475 a.C.) Tot de geometrie is de beroemde stelling van Pythagoras, die vaststelt dat binnen een rechthoek driehoek het vierkant van de hypotenuse (de zijde tegenover de rechte hoek) gelijk is aan de som van de vierkanten van de resterende zijden.

Elementen van Euclid

Het meest prominente werk dat sinds de oudheid is gered, is de studie geweest De elementen, van Euclid de Alejandría (325 a.C. - 265 A.C.), gemaakt in de 300s tot.C. Het is een werk van geweldige historische waarde die al meer dan 2000 jaar als basis voor het onderwijzen van wiskunde heeft gediend.

Euclid

De elementen Het was een van de eerste boeken en compilaties van studies die wiskundige principes verklaarden die op elke situatie konden worden toegepast. Inclusief postulaten, die de fundamentele principes van geometrie zijn in hun werk. Aan de andere kant zijn er de kwantitatieve principes die bekend staan ​​als de basisbegrippen.

Euclid -onderwijs verminderde bouwinstrumenten binnen geometrie tot slechts twee: een regel zonder maatregelen en een kompas. Dit genereerde de drie klassieke problemen die geen antwoorden vonden tot de negentiende eeuw: de kwadratuur van de cirkel, de duplicatie van de kubus en de trisectie van een hoek. 

Kan je van dienst zijn: in welke eeuw veroverden de Spanjaarden Tenochtitlán?

Voor de ouden waren de twee ideale geometrische entiteiten de rechte lijn en de cirkel, dus de meeste geometrische stellingen die werden voorgesteld waren het product van verkenning met deze instrumenten.

Geometrie in astronomie

De geometrie profiteerde ook voor de Grieken in termen van de studie van de sterren. Ze berekenden de bewegingen door de observatie en maakten geometrische vlakken van de hemel die de aarde vestigden als een centraal punt, en zowel de zon als de maan en de andere planeten en entiteiten die eromheen bewogen, roteerden in een reeks cirkels. 

Een van de meest invloedrijke bijdragen was de Almagest, Geschreven in de tweede eeuw D.C door Claudio Ptolemy (100 D. C.- 170 d.C), een astronomisch verdragscontainer van de sterrencatalogus. Het was de meest complete tekst van zijn tijd en beïnvloedde astronomische studies op een transcendentale manier tot de middeleeuwen zeer geavanceerd. Het maakte deel uit van de media die het geocentrische systeem het meest populair maakten, dat beweerde dat de aarde het centrum van het universum was.

Ptolemaeus

Islamitische invloed

Tegen de IX eeuwen, toen de Arabische wereld in zijn grote uitbreiding was, doordrong veel van zijn cultuur verschillende gebieden van wetenschap en kunst. Ze waren geweldige fans van de wiskundige en filosofische werken van de Grieken. 

Een van de meest onderzochte takken in hun behoeften was astronomie, om de exacte oriëntatie te vinden waarin MECA de zinnen moest uitvoeren.

In navolging van de studies van Euclid en andere bijdragen zoals die van Ptolemy, ontwikkelden moslims de stereografische projectie, dat wil zeggen de projectie van de hemelse sfeer in het vlak om het als een kaart te gebruiken. Dit betekende vooruitgang met betrekking tot de studie van trigonometrie.

Een van de meest representatieve karakters is Thābit ibn Qurra (826/36-901) die relevante vertalingen maakte van de oude teksten van Apollonius, Archimedes, Euclid en Ptolemy. Sommige hiervan zijn de enige overlevende versies van oude geschriften.

De verkenningen met betrekking tot astronomische geometrie maakten ook het maken van een van de meest representatieve instrumenten, de Astrolabio, die de astronomische berekeningen van het moment vereenvoudigde. Bovendien liet dit instrument hen ook toe om tijd te weten en uiteindelijk de begeleiding voor MECA te krijgen. 

Het kan u van dienst zijn: 8 douane en tradities van de mixtecs

Europese Legacy Development

In de twaalfde eeuw, na het invoegen van de klassieke leer van de Grieken dankzij de moslimuitbreiding en de ontwikkeling van dezelfde ontdekkingen, begonnen vertalingen van Latijnse teksten rechtstreeks uit het Grieks rechtstreeks uit het Grieks of van de Arabische taal te worden gemaakt. 

Dit zou plaats maken voor een nieuw leren in Europa dat door de Renaissance zou worden gepromoot. De herontdekking van noties zoals het "bewijsmateriaal" begon, een concept ontwikkeld onder de Grieken die geïnteresseerd was in de demonstratie van de postulaten in de realiteit.

Geometrie in kunst

Kennis werd ook weerspiegeld in de kunst, zoals schilderen of architectuur, omdat geometrie een fundamenteel onderdeel zou worden van de ontwikkeling van perspectief in kunst.

Filippo Brunelleschi (1377-1446), was degene die erin slaagde het lineaire perspectief te ontwikkelen via wiskunde. Het doel van deze theorie was om in een vlak een drie -dimensionale ruimte te vertegenwoordigen van hoe het door het menselijk oog werd waargenomen. Daarom stelt het vast dat alle lijnen in een foto moesten samenkomen of een lekkage vinden om het gevoel van diepte te genereren. 

Filippo Brunelleschi. Bron: I, Sailko/CC BY-S (http: // creativeCommons.Org/licenties/by-sa/3.0/)

Brunelleschi was de eerste die het perspectief beschreef als een wetenschappelijke procedure en dit werkte als basis van latere banen in de kunst.

Binnen andere voorbeelden van de toepassing van geometrie op de studie van kunst en de mens op zichzelf, is het werk van Leonardo da Vinci (1452-1519) in zijn tekening De Vitruvio -man. Het is een onderzoek gebaseerd op de meest perfecte verhoudingen voor het menselijk lichaam door een geometrische analyse van zijn structuur.

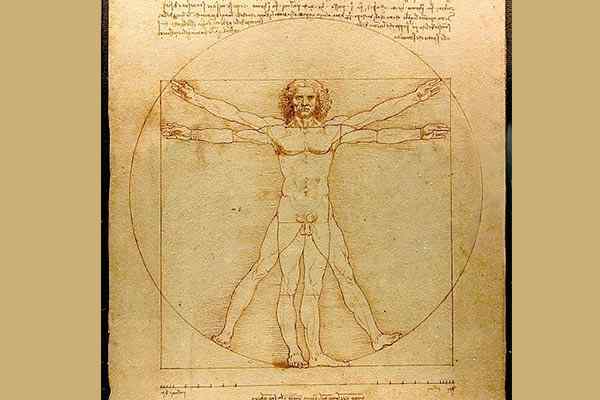The Man of Showcase van Leonardo Da Vinci / Public Domain

Onder andere valt architectuur ook op, waar verschillende elementen zoals symmetrie en balans begonnen te verschijnen als fundamentele kenmerken. Vierkante, rechthoekige deuren en ramen, op een evenwichtige manier geplaatst; Gebruik van klassieke elementen van de oudheid zoals kolommen, koepels en kluizen.

Stap naar de moderniteit

De analyse van perspectieven en projecties tijdens de Renaissance was een van de prikkels om het belang van wiskundigen op te wekken. Vanaf dit moment beginnen meer solide en complexe wiskundige bases te worden gebaseerd in geometrie.

Een van de belangrijkste werken voor de moderniteit was die van de architect Girard ontwapend (1591-1661), die het begin voor projectieve geometrie veronderstelde. Enerzijds stelde het vast dat de parallelle lijnen in een projectie moeten samenkomen op een punt op de Infinity -lijn, dat wil zeggen de horizon.

Kan u van dienst zijn: Tuxtepec Rebellion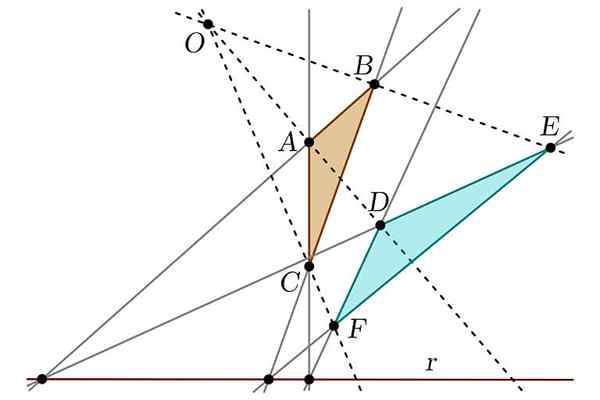Verwijdering Stelling

Aan de andere kant ontdekte hij ook wat zou worden erkend als de verontrustingsstelling van de verontruster, die de relatie tot stand brengt tussen twee figuren die als "projectief" kunnen worden beschouwd. Het was ook verantwoordelijk voor het vereenvoudigen van de werken van Apollonius met betrekking tot de secties van een kegel, waardoor analogieën tussen deze figuur en de cilinder waren.

Een andere geweldige gebeurtenis van de periode was het creëren van analytische geometrie door de studies van René Descartes (1596-1650) en Pierre de Fermat (1601-1665) onafhankelijk. Dit is de studie van geometrie door het gebruik van een coördinatensysteem. 

René Descartes werkt op uw bureaublad. Wikimedia Commons

Niet -Euclidian geometrie

Tegen de 18e en 19e eeuw begonnen studies in niet -Euclidian geometrie. In het bijzonder waren Gauss, Johann Boleai en Lobachevski, die ontdekten dat het vijfde postulaat van Euclid, bekend als parallel postulaat, niet konden worden geverifieerd.

Op deze manier ontwikkelden ze een soort geometrie waarin dit postulaat gekwalificeerd was als onwaar. Deze nieuwe vorm was succesvol door bevredigende resultaten te geven in geometriestijlen die niet noodzakelijkerwijs alle Euclid -postulaten hebben ontmoet. Zo werden hyperbolische geometrie en elliptische geometrie later geboren.

Het is de moeite waard om het werk van Leonhard Euler (1707-1783) in de 18e eeuw te benadrukken, met betrekking tot de ontwikkeling van wiskundige notatie. Vervolgens zou de twintigste eeuw de ontwikkeling van meer specifieke gebieden van geometrie met zich meebrengen waaronder:

-Algebraïsche geometrie: Het is een tak van wiskunde die abstracte algebra en analytische geometrie combineert.

-Eindige geometrie: Het is een geometrisch systeem dat bestaat uit een eindige hoeveelheid punten, dat wil zeggen dat ze een einde of limiet hebben en daarom kunnen ze worden gemeten.

-Digitale geometrie: Het is een tak van informatica die de studie van algoritmen en datastructuren die in geometrische termen kunnen worden weergegeven. 

Referenties

1. (2016) Wat Euclid -elementen het enige boek maakte dat kan concurreren met de Bijbel. BBC. BBC is hersteld.com
2. De drie klassieke problemen van de Griekse wiskunde. Universiteit van Antioquia. Hersteld van lesgeven.Jij.Edu.co
3. Heilbron J.L (2020). Geometrie. Encyclopædia Britannica. Hersteld uit Britannica.com
4. Geschiedenis van geometrie. Wikipedia, de gratis encyclopedie. Opgehaald van.Wikipedia.borg
5. Analytische meetkunde. Wikipedia, de gratis encyclopedie. Opgehaald van.Wikipedia.borg
6. (2017) Geometrie en wiskunde in de Renaissance. Hersteld van ukessays.com
7. Sáiz a. Lineair perspectief in Brunelleschi. Universiteit van Valencia. UV hersteld.is
8. De redacteuren van Encyclopaedia Britannica (2019). Renaissance -architectuur. Encyclopædia Britannica. Hersteld uit Britannica.com
9. Andersen K (2020). Girard ontwapende. Encyclopædia Britannica. Hersteld uit Britannica.com
10. (2011) Een interessante inleiding tot computationele geometrie. Opgehaald van Gaussians.com