Wiskunde

Vectorfuncties

3312
22
Lonnie Rohan

Wat zijn vectorfuncties?

A vectorfunctie van een parameter T, Het is een functie waarvan het domein de werkelijke waarden is van T, Terwijl de route wordt gevormd door vectoren van de vorm R ((T)). Een dergelijke functie kan worden uitgedrukt als:

R ((T) = f (T)) Je + G (T)) J + H (T)) k

Waar Je, J En k Ze zijn de eenheidsvectoren in de drie hoofdrichtingen van de ruimte, en de functies F, G en H zijn echte functies van de variabele T. De notatie maakt gebruik van vetgedrukte, om vectorgroottes te onderscheiden.

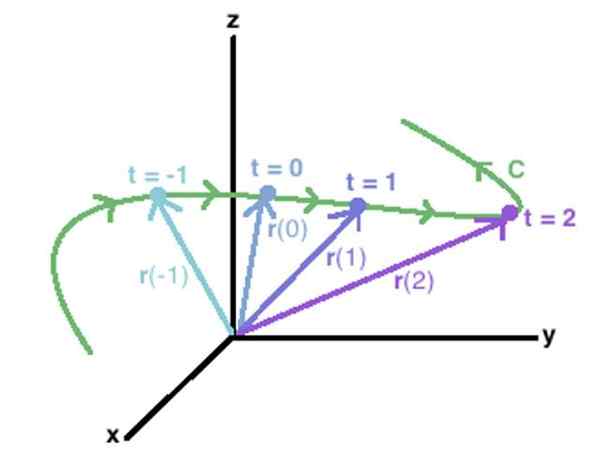Een vectorfunctie in de ruimte kan worden gebruikt om een C -curve te beschrijven, waarbij de extreme punten worden samengevoegd van elk van de vectoren bepaald door die functie. Bron: Wikidot.

Een andere manier om een vectorfunctie aan te geven, is door vierkante haakjes:

R ((T) = T), G (T), H (T)>

Vectorfuncties kunnen worden gebruikt om curven in het vlak en de ruimte te bestuderen, zoals het traject dat een bewegend object volgt. Een voorbeeld is de gelijkenis beschreven door een geprojecteerde bal met initiële snelheid, onder zwaartekracht.

Als je de positie van de bal op elk moment van tijd wilt weten T, De vectorfunctie met twee componenten, één horizontaal en één verticaal:

R ((T) = x (T)) Je + En(T)) J

Beide x (T) als y (T) Het zijn tijdfuncties T. Dus bij het samenvoegen van de extreme punten van elk van de vectoren R((T) Mogelijk, vorm de gelijkenis die door de bal in het vliegtuig wordt beschreven XY.

Het concept strekt zich gemakkelijk uit tot een C -curve in de ruimte, zoals die in de bovenstaande figuur. Vectoren verschijnen erin R (-1), R (0), R (1) R (2), waarvan de uiteinden de C -curve trekken, in groen getrokken.

Limieten, afgeleid en integraal van vectorfuncties

Berekeninghulpmiddelen die van toepassing zijn op echte reële variabele functies kunnen ook worden toegepast op vectorfuncties.

Kan u van dienst zijn: factorisatie

Limiet van een vectorfunctie

De vectorfunctielimiet R ((T) = f (T)) Je + G (T)) J + H (T)) k, Wanneer T → A, wordt het gedefinieerd als:

$\dpi110 \displaystyle \lim_t \to a\textbfr(t)=\left [ \displaystyle \lim_ t\to a f(t)\right ]\textbfi+\left [ \displaystyle \lim_ t\to a g(t)\right ]\textbfj+\left [ \displaystyle \lim_ t\to a h(t)\right ]\textbfk$

Ervan uitgaande dat er de respectieve limieten van f zijn (T), G (T) en h (T), wanneer T → a.

Afgeleid van een vectorfunctie

De definitie van afgeleid van een vectorfunctie R (t) = f (T)) Je + G (T)) J + H (T)) k Het is analoog aan die van de afgeleide van een echte functie van echte variabele. Roeping R'(T) tot genoemde afgeleide, je hebt:

$\dpi110 \mathbfr'(t)=\displaystyle \lim_\Delta t \to 0\frac\mathbfr(t+\Delta t)-\mathbfr(t)\Delta t$

Het afgeleide bestaat wanneer de vorige limiet bestaat, en zo ja, de functie R((T) is onderscheidbaar in T.

Integraal van een vectorfunctie

Zijn R (t) = f (T)) Je + G (T)) J + H (T)) k een vectorfunctie, zodat functies F, G en H integreerbaar zijn in T.

Dus:

$\dpi110 \int \mathbfr(t)dt =\left [ \int f(t)dt \right ]\mathbfi+\left [ \int g(t)dt \right ]\mathbfj+\left [ \int h(t)dt \right ]\mathbfk+\mathbfC$

Met:

C = c₁Je + C₂J

Wat betekent dat de integratieconstante ook een vector is, maar constant.

Voorbeelden van vectorfunctie

voorbeeld 1

U hebt de vectorfunctie gegeven door R ((T) = 3sec T Je + 2TAN T J. Het is mogelijk om het te evalueren voor verschillende t -waarden, zoals t = π/4 en t = π, wat aanleiding geeft tot vectoren R (π/4) en R (π):

R (π/4) = 3sec (π/4) Je + 2tan (π/4) J = 3√2 Je + 2 J

R (π) = 3sec (π) Je+2tan (π) J = - 3 Je

Echter, R ((T) Het bestaat niet voor waarden van t = ∓π/2, ∓3π/2, ∓5π/2 ..., aangezien de SEC -functie T = 1 /cos T Het is niet gedefinieerd, het is ook zo T = Sen T / Cos T.

Daarom is het domein van de R (t) -functie alle reële waarden van t, behalve die van de vorm:

∓ (2n+1) π/2; Met n = 0, 1, 2, .. .

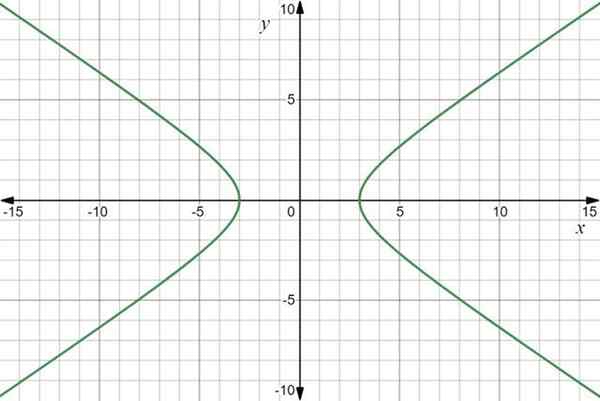
De grafiek van de functie is een hyperbool:

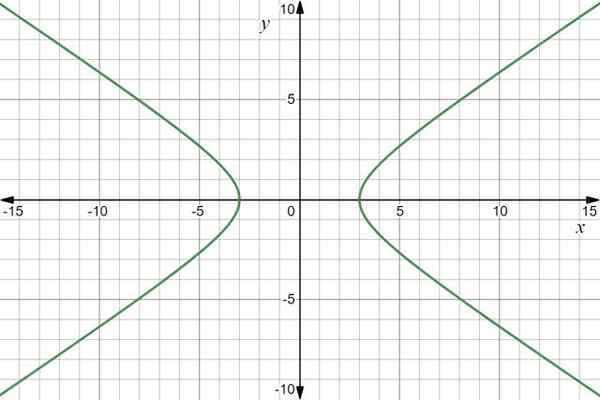Vectorfunctie grafiek R (t) = 3sec t Je+2 tan t J. Bron: f. Zapata via Desmos.

Voorbeeld 2

In de hellende projectiellancering is de mobiele positie de vectorfunctie R ((T) = x (T)) Je + En(T)) J . Ervan uitgaande dat luchtweerstand niet tussenbeide komt, en dat zwaartekracht de enige kracht is die op de mobiel werkt, is de horizontale beweging uniform rechtlijnig, terwijl de verticaal uniform wordt versneld, zijnde g = 9.8 m/s² De versnellingswaarde. Deze versnelling is verticaal tegen de grond.

Kan u van dienst zijn: afleidingregels (met voorbeelden)

In dit geval zijn de functies x (T) En (T) Ze zijn respectievelijk:

x (t) = x_of + v_os∙ t
en (t) = y_of + v_Oy∙ t - ½ gt²

De hoeveelheden v_os en v_Oy Ze zijn de componenten van de vectorfunctie die de mobiele snelheid te allen tijde beschrijft:

v ((T) = V_X((T)) Je + v_En((T)) J

Met:

v_os = V_of∙ cos θ
v_Oy = V_of∙ Sen θ

Zijnde θ de hoek die de beginsnelheid vormt ten opzichte van de horizontale.

Van zijn kant is de initiële positie van de mobiel het coördinaatpunt (x_of,En_of), of gelijkwaardig, de positievector gegeven door:

R_of ((T) = x_of Je + En_of J

Merk op dat, in de getoonde vergelijkingen, een negatief teken is toegewezen aan de verticale richting, dus de derde term van de vergelijking voor y (t) neemt het. Het is ook mogelijk om de oorsprong toe te wijzen aan de beginpositie van de mobiel.

Directe snelheid van projectiel

De momentane snelheid V (t) is de eerste afgeleid van de positie, ten opzichte van de tijd. Het wordt berekend door de bekende afleidingregels toe te passen:

v(t) = R ' ((T) = [x (T)) Je + En(T)) J]'= X '(T)) Je + En'(T)) J = v_osJe + (v_Oy - GT) J

De snelheidsmodule wordt gegeven door:

$\dpi110 \left|\textbfv \right|=\sqrtv_ox^2+v_oy^2$

Onmiddellijke versnelling van het projectiel

Het is bekend dat het g is, in verticale richting en richting naar beneden. Dit wordt geverifieerd, wetende dat versnelling de eerste afgeleide van snelheid is ten opzichte van de tijd (of de tweede afgeleide van de positie ten opzichte van de tijd, indien voorkeur):

naar(t) = V ' ((T) = [V_osJe + (v_Oy - GT) J] '= [V_osJe] '+ [(v_Oy - GT) J] '= = - G J

Dit is precies het verwachte resultaat.

Oefening opgelost

Gezien de vectorfunctie R ((T) = 3T Je + (T - 1) J, vinden R '(t) en R "(T).

Oplossing

Als u de afleidingregels op elk van de componenten toepast, hebt u:

Kan u van dienst zijn: Integratieconstante: betekenis, berekening en voorbeelden

R '(t) = = 3 Je + J

En omdat de afgeleide van een constante 0 is:

R "(t) = 0

Het is te zeggen, R "(t) is gelijk aan de nulvector.

Referenties

Figueroa, D. 2005. Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB).
Larson, r. Berekening met analytische geometrie. 2e. Editie. McGraw Hill.
Mathonline. Vector-waargenomen functies. Hersteld van: Mathonline.Wikidot.com.
Openentax. CALCULUS VOLUME 3. Opgehaald uit: OpenStax.borg.
Purcell, E. J. 2007. Berekening. Pearson Education.