Overjectieffunctie, eigenschappen, voorbeelden

A overagentieffunctie Het is elke relatie waarbij elk element dat tot codominium behoort een beeld is van ten minste één domeinelement. Ook bekend als functie over, Ze maken deel uit van de classificatie van functies met betrekking tot de manier waarop hun elementen gerelateerd zijn.

Bijvoorbeeld een functie F: a → B gedefinieerd door F (x) = 2x

Die wordt gelezen "F dat gaat van NAAR tot B gedefinieerd door F (x) = 2x "

Touch Definieer de start- en aankomstsets A en B.

A: 1, 2, 3, 4, 5 Nu zullen de waarden of afbeeldingen die elk van deze elementen worden vrijgegeven wanneer deze worden geëvalueerd F, Zij zullen de elementen van Codominium zijn.

F (1) = 2

F (2) = 4

F (3) = 6

F (4) = 8

F (5) = 10

Dus het vormen van de set B: 2, 4, 6, 8, 10

Het kan dan worden geconcludeerd dat:

F: 1, 2, 3, 4, 5  → 2, 4, 6, 8, 10 gedefinieerd door F (x) = 2x is een overjectieffunctie

Elk element van het codominium moet ten minste één bewerking van de onafhankelijke variabele zijn via de functie in kwestie. Er is geen beeldbeperking, een element van codominium kan een beeld zijn van meer dan één element van het domein en blijven omgaan met een overagentieffunctie.

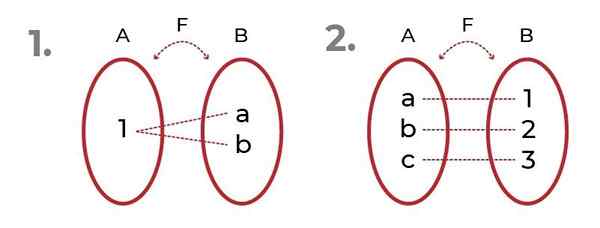
De afbeelding toont 2 voorbeelden met Onjectieve functies.

Bron: auteur

In het eerste wordt opgemerkt dat de afbeeldingen naar hetzelfde element kunnen worden verwezen, zonder de Overtolligheid van de functie.

In het tweede zien we een billijke verdeling tussen domein en afbeeldingen. Dit geeft aanleiding tot Bijectieve functie, waar de criteria van Injectieve functie en overjectieffunctie.

Een andere methode om te identificeren Onjectieve functies, is om te verifiëren of het codominium gelijk is aan de rang van de functie. Dit betekent dat als de aankomstset gelijk is aan de afbeeldingen die door de functie worden geleverd bij het evalueren van de onafhankelijke variabele, De functie is overjectief.

[TOC]

Eigenschappen

Overwegen Overtuigen Het volgende moet worden vervuld tot een functie:

Zijn F: D_F → C_F

∀ B ℮ C_F  EN naar ℮  D_F   / F (a) = b

Dit is de algebraïsche manier om dat vast te stellen Voor alle "B" die tot C behoort_F Er is een "A" die bij D hoort_F  zodanig dat de F -functie geëvalueerd in "A" gelijk is aan "B". 

Het kan u van dienst zijn: radicale eigenschappen

Overjectiviteit is een eigenaardigheid van functies, waarbij codominium en rang vergelijkbaar zijn. Aldus vormen de elementen die in de functie worden geëvalueerd de aankomstset vormen.

Conditionering van functies

Soms een functie die niet is Overtuigen, kan bepaalde conditionering ondergaan. Deze nieuwe voorwaarden kunnen er een van een overagentieffunctie.

Alle soorten wijzigingen in het domein en het codominium van de functie zijn geldig, waarbij het doel is om te voldoen aan de overheidseigenschappen in de overeenkomstige relatie.

Voorbeelden: opgeloste oefeningen

Om aan de voorwaarden te voldoen van Overtolligheid Verschillende conditioneringstechnieken moeten worden toegepast, dit om ervoor te zorgen dat elk element van het codominium zich binnen de set afbeeldingen van de functie bevindt.

Oefening 1

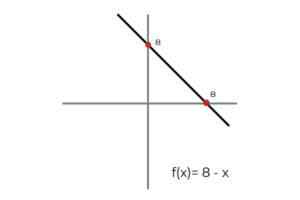
• Wees de functie F: R → R gedefinieerd door de lijn F (x) = 8 - x

A: [Alle reële getallen]

Bron: auteur

In dit geval beschrijft de functie een continue lijn, die alle reële getallen bestrijkt, zowel in hun domein als in het bereik. Omdat de rang van de functie R_F Het is gelijk aan codominium R Het kan worden geconcludeerd dat:

F: R → R gedefinieerd door de lijn F (x) = 8 - x is een overagentieffunctie.

Dit is van toepassing op alle lineaire functies (functies waarvan de grotere mate van de variabele één is).

Oefening 2

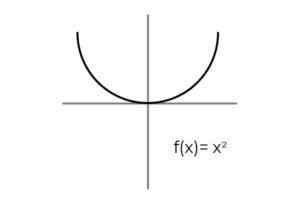
• Bestudeer de functie F: R → R gedefinieerd door F (x) = x² : Definieer of het een overagentieffunctie. In het geval dat niet zo is, toon de nodige conditionering om het te overwinnen.

Bron: auteur

Het eerste wat u moet overwegen is het codominium van F, die bestaat uit reële cijfers R. Er is geen manier voor de functie om een ​​negatieve waarde te gooien, die negatieve reële uitsluiting onder mogelijke afbeeldingen.

Conditionering van het intervalcodominium [0 , ∞ ]. Het wordt vermeden om elementen van de co -alomio te verlaten zonder ermee te relateren F.

De afbeeldingen worden herhaald voor paren van elementen van de onafhankelijke variabele, zoals x = 1 En x = - 1.  Maar dit heeft alleen invloed op de Injectiviteit  van de functie, geen probleem zijn voor deze studie.

Kan u van dienst zijn: opeenvolgende derivaten

Op deze manier kan worden geconcludeerd dat:

F: R  →[0, ∞ )) gedefinieerd door F (x) = x²    Het is een overjectieffunctie

Oefening 3

• Definieer de voorwaarden van het codominium dat ze zouden doen overtuigen naar functies

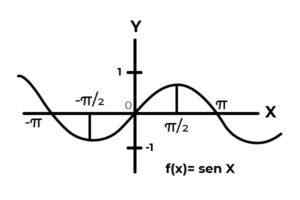
F: R  → R gedefinieerd door F (x) = sin (x)

F: R  → R gedefinieerd door F (x) = cos (x)

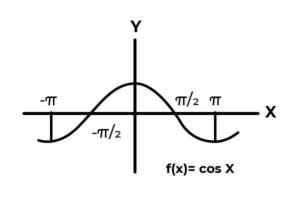Bron: auteur Bron: auteur.

Het gedrag van trigonometrische functies is vergelijkbaar met dat van golven, die heel gebruikelijk is om herhalingen van de afhankelijke variabele tussen de afbeeldingen te vinden. Ook in de meeste gevallen is het bereik van de functie beperkt tot een of meer sectoren van de echte lijn.

Dit is het geval van sinus- en cosinusfuncties. Waar hun waarden fluctueren in het interval [-1, 1]. Dit interval moet het codominium conditioneren om de envelop van de functie te bereiken.

F: R  →[ -elf ] gedefinieerd door F (x) = sin (x)  Het is een overjectieffunctie

F: R  →[ -elf ]gedefinieerd door F (x) = cos (x) Het is een overjectieffunctie

Oefening 4

• Bestudeer de functie

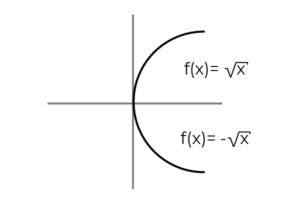
F: [0, ∞ )) → R gedefinieerd door F (x) = ± √x   Geef aan of het een overagentieffunctie

Bron: auteur

De functie F (x) = ± √x  Het heeft de bijzonderheid die 2 afhankelijke variabelen definieert bij elke waarde van "x" . Dat wil zeggen, het bereik ontvangt 2 elementen voor elk dat in het domein wordt uitgevoerd. Een positieve en negatieve waarde voor elke waarde van "x" moet worden geverifieerd voor elke waarde van "x".

Bij het observeren van de startassemblage wordt opgemerkt dat het domein al is beperkt, dit om de onbeperkingen te voorkomen die worden geproduceerd bij het evalueren van een negatief getal in een koppelwortel.

Bij het verifiëren van het bereik van de functie laat zien dat elke codominiumwaarde tot het bereik behoort.

Op deze manier kan worden geconcludeerd dat:

F: [0, ∞ )) → R gedefinieerd door F (x) = ± √x  Het is een overjectieffunctie

Kan u van dienst zijn: Gelijktijdige vectoren: kenmerken, voorbeelden en oefeningen

Oefening 4

• Bestudeer de functie F (x) = ln x  Geef aan of het een overagentieffunctie. Conditie De aankomst en vertrek stelt in om de functie aan te passen aan de criteria van overjectiviteit.

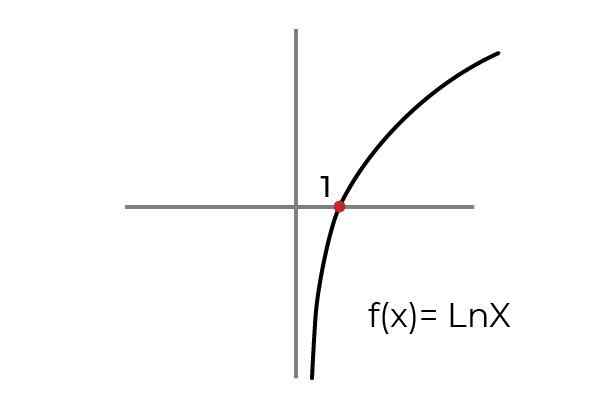Bron: auteur

Zoals weergegeven in de grafiek de functie F (x) = ln xwordt gedefinieerd voor de waarden van "x" groter dan nul. Terwijl de waarden van "en" of afbeeldingen elke reële waarde kunnen nemen.

Op deze manier kunnen we het domein van F (x) = tot het interval (0 , ∞ ))

Terwijl de rang van de functie kan worden gehandhaafd als een reeks reële getallen R.

Gezien dit kan worden geconcludeerd dat:

F: [0, ∞ )) → R gedefinieerd door F (x) = ln x  Het is een overjectieffunctie

Oefening 5

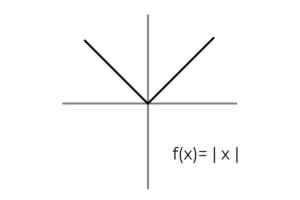
• Bestudeer absolute waardefunctie F (x) = | X | en wijs de aankomst- en vertreksets aan die zijn verzameld voor de criteria voor allegiviteit.

Bron: auteur

Het domein van de functie is vervuld voor alle reële getallen R. Op deze manier moet de enige conditionering worden uitgevoerd in het codominium, rekening houdend met dat de absolute waardefunctie alleen positieve waarden nodig heeft.

Het codominium van de functie is vastgesteld dat het gelijk is aan het bereik van hetzelfde

[0 , ∞ ))

Nu kan worden geconcludeerd dat:

F: [0, ∞ )) → R gedefinieerd door F (x) = | X |  Het is een overjectieffunctie

Voorgestelde oefeningen

1. Controleer of de volgende functies overjectief zijn:

• F: (0, ∞ )) → R gedefinieerd door F (x) = log (x + 1)
• F: R → R gedefinieerd door F (x) = x³
• F: R →[1, ∞ ))  gedefinieerd door F (x) = x²  + 1
• [0, ∞ )) → R gedefinieerd door F (x) = log (2x + 3)
• F: R → R gedefinieerd door F (x) = sec x
• F: r - 0 → R gedefinieerd door F (x) = 1 / x

Referenties

1. Inleiding tot logica en kritisch denken. Merrilee h. Zalm. Universiteit van Pittsburgh
2. Problemen in wiskundige analyse. Piotr Barar, Alfred Witkowski. Universiteit van Wroclaw. Pool.
3. Elementen van abstracte analyse. Mícheál O'Searcoid PhD. Afdeling Wiskunde. University College Dublin, Beldfield, Dublind 4
4.  Inleiding tot logica en de methodologie van de deductieve wetenschappen. Alfred Tarski, New York Oxford. Oxford Universiteit krant.
5.  Wiskundige analyseprincipes. Enrique Linés Escardó. Redactionele terugvordering. Tot 1991. Barcelona, ​​Spanje.