Logaritmische functie -eigenschappen, voorbeelden, oefeningen

De logaritmische functie Het is een wiskundige relatie die elk positief reëel getal associeert X Met uw logaritme En op een basis naar. Deze relatie voldoet aan de vereisten om een ​​functie te zijn: elk element X dat bij het domein behoort, heeft een uniek beeld.

Daarom:

f (x) = y = log_naar X , Met een> 0 en verschillend van 1.

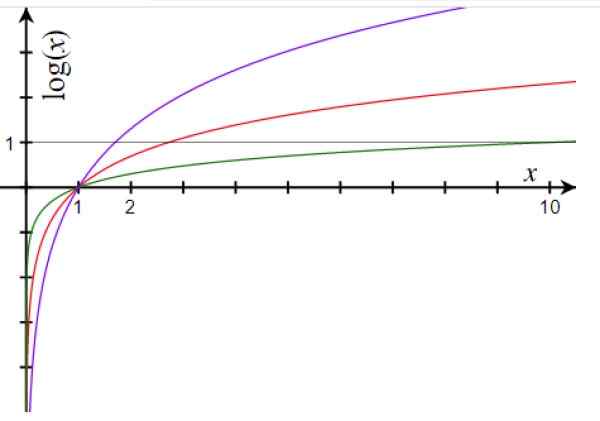
Figuur 1. Logaritm -functiegrafiek voor basis 10 (groen), basis E (rood) en basis 1.7 (paars). Bron: Wikimedia Commons.

De belangrijkste eigenschappen van logaritmische functie zijn:

-Het domein zijn allemaal de reacter groter dan 0, exclusief 0. Met andere woorden, er is geen logaritme of negatieve getallen op een basis. In de vorm van een interval:

Zon _F = (0, ∞+)

-De logaritme van een getal kan negatief, positief of 0 zijn, zodat het bereik of de route is:

RGO _F = (-∞, ∞+)

-Logaritmische functie groeit altijd voor een> 1 en daalt<1.

-Het omgekeerde van f (x) = logboek_naar X is de exponentiële functie.

Inderdaad, de logaritm -functie op basis van, is de omgekeerde functie van de potentiële functie:

F^-1(x) = a^En

Sinds Logaritm gebaseerd naar van een nummer X, Het is het nummer En waarnaar de basis moet worden verhoogd naar krijgen X.

-De basislogaritme is altijd 1. Dus de grafiek van f (x) = logboek_naar X Elkaar altijd kruisen naar de X -as op het punt (1.0)

-De logaritmische functie is transcendent en kan niet worden uitgedrukt als polynoom of als een quotiënt hiervan. Naast logaritme bevat deze groep onder andere trigonometrische en exponentiële functies.

[TOC]

Voorbeelden

De logaritmische functie kan worden vastgesteld via verschillende bases, maar de meest gebruikte zijn 10 en En, waar En Het is het aantal Euler gelijk aan 2.71828 .. .

Wanneer de basis 10 wordt gebruikt, wordt de logaritme decimale logaritme, vulgaire logaritme, briggs of gewoon logaritm genoemd om te drogen.

En als het nummer E wordt gebruikt, wordt het Neperian Logaritm genoemd, door John Napier, de Schotse wiskundige die de logaritmen ontdekte.

Kan u van dienst zijn: multiplicatief inverse: uitleg, voorbeelden, opgeloste oefeningen

De voor elk gebruikte notatie is als volgt:

-Decimale logaritme: logboek₁₀ x = log x

-Neperian Logaritm: ln x

Wanneer een andere basis zal worden gebruikt, is het absoluut noodzakelijk. Als het bijvoorbeeld gaat over logaritmen op basis 2, is er geschreven:

y = log₂ X

Laten we eens kijken naar het nummer 10 -logaritme in drie verschillende bases, om dit punt te illustreren:

Log 10 = 1

ln 10 = 2.30259

aanroepen₂ 10 = 3.32193

Gemeenschappelijke rekenmachines brengen alleen decimale logaritmen (log) en Neperian Logaritm (LN -functie). Op internet zijn er rekenmachines met andere bases. In elk geval kan de lezer, met de hulp daarvan, verifiëren dat deze met de vorige waarden wordt vervuld:

10¹ = 10

En^2.3026 = 10.0001

2^3.32193 = 10.0000

Kleine decimale verschillen zijn te wijten aan de hoeveelheid decimalen die zijn genomen bij de berekening van de logaritme.

De voordelen van logaritmen

Een van de voordelen van het gebruik van de logaritmen is het gemak dat ze bieden om met grote getallen te werken, met behulp van hun logaritme in plaats van het nummer rechtstreeks.

Dit is mogelijk omdat de logaritm -functie langzamer groeit naarmate de cijfers groter zijn, zoals we in de afbeeldingen waarderen.

Dus zelfs in het geval van zeer grote getallen zijn hun logaritmen veel kleiner en het manipuleren van kleine aantallen is altijd eenvoudiger.

Bovendien voldoen de logaritmen aan de volgende eigenschappen:

-Product: log (a.b) = log a + log b

-Quotiënt: log (a/b) = log a - log b

-Stroom: log a^B = B.Log a

En op deze manier worden producten en quotiënten bedragen en aftrekking van kleinere aantallen, terwijl de potentiëring wordt omgezet in een eenvoudig product, hoewel de kracht hoog is.

Dat is de reden waarom de logaritmen het toelaten om getallen uit te drukken die variëren in zeer grote waardenbereiken, zoals de intensiteit van het geluid, de pH van een oplossing, de helderheid van de sterren, de elektrische weerstand en de intensiteit van de aardbevingen op de Richter schaal.

Kan u van dienst zijn: externe alternatieve hoeken: oefeningen en oefeningen opgelostFiguur 2. Logaritmen worden op de schaal van Richter gebruikt om de grootte van aardbevingen te kwantificeren. De afbeelding toont een gebouw dat is ingestort in Concepción, Chili, tijdens de aardbeving van 2010. Bron: Wikimedia Commons.

Laten we eens kijken naar een voorbeeld van de behandeling van de eigenschappen van de logaritmen:

Voorbeeld

Zoek de waarde van X in de volgende uitdrukking:

log (5x +1) = 1 + log (2x-1)

Antwoord

We hebben hier een logaritmische vergelijking, gezien het feit dat het onbekende zich op het argument van Logaritm bevindt. Het wordt opgelost door een enkele logaritme aan elke kant van gelijkheid achter te laten.

We beginnen met het plaatsen van alle termen die "x" links van gelijkheid bevatten, en die die alleen nummers aan de rechterkant bevatten:

log (5x+1) - log (2x -1) = 1

Aan de linkerkant hebben we de aftrekking van twee logaritmen, die kunnen worden geschreven als de logaritme van een quotiënt:

log [(5x+1)/ (2x-1)] = 1

Aan de rechterkant is echter nummer 1, dat we kunnen uitdrukken als log 10, zoals we eerder zagen. Dus:

log [(5x+1)/ (2x-1)] = log 10

Om gelijkheid te vervullen, de argumenten van de logaritmen moet hetzelfde zijn:

(5x+1)/ (2x-1) = 10

5x + 1 = 10 (2x - 1)

5x + 1 = 20 x - 10

-15 x = -11

x = 11/15

Application Oefening: Richter's Scale

In 1957 vond een aardbeving plaats in Mexico wiens omvang 7 was.7 op de schaal van Richter. In 1960 vond een andere aardbeving voor de meest magnitude plaats in Chili, 9.5.

Bereken hoe vaak de Chileense aardbeving intenser was dan die van Mexico, wetende dat de omvang M_R Op de schaal van Richter wordt het gegeven door de formule:

M_R = log (10⁴ Yo)

Oplossing

De omvang in de Richter -schaal van een aardbeving is een logaritmische functie. We gaan de intensiteit van elke aardbeving berekenen, omdat we de Richter -magnitudes hebben. Laten we het stap voor stap doen:

Kan u van dienst zijn: Primo -nummers: kenmerken, voorbeelden, oefeningen

-Mexico: 7.7 = log (10⁴ Yo)

Aangezien het omgekeerde van de logaritm -functie de exponentiële is, passen we dit toe aan beide zijden van gelijkheid met de bedoeling om I te wissen, dat wordt gevonden in het Logaritm -argument.

Omdat het decimale logaritmen zijn, is de basis 10. Dus:

In de term van rechts, 10 en log (10⁴ I) Ze worden geannuleerd (zoals bij de vierkante en vierkante wortel), zijn: vertrekken:

10 ^7.7 = 10⁴ Je

De intensiteit van de aardbeving van Mexico was:

Je_M = 10 ^7.7 / 10⁴ = 10^3.7

 -Chili: 9.5 = log (10⁴ Yo)

Dezelfde procedure leidt ons tot de intensiteit van de Chileense aardbeving i_Ch:

Je_Ch = 10 ^9.5 / 10⁴ = 10^5.5

 Nu kunnen we beide intensiteiten vergelijken:

Je_Ch / Yo_M = 10^5.5 / 10^3.7 = 10^1.8 = 63.1

 Je_Ch = 63.1. Je_M

Chili's aardbeving was ongeveer 63 keer intenser dan Mexico. Omdat de grootte logaritmisch is, groeit het langzamer dan intensiteit, dus een verschil van 1 in grootte betekent een 10 keer grotere amplitude van de seismische golf.

Het verschil tussen de grootten van beide aardbevingen is 1.8, daarom zouden we een verschil in intensiteiten kunnen verwachten dichter bij 100 dan tot 10, zoals effectief is gebeurd.

In feite, als het verschil precies 2 was geweest, zou de Chileense aardbeving 100 keer intenser zijn geweest dan de Mexicaan.

Referenties

1. Carena, m. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Presiversity wiskundehandleiding. Nationale Universiteit van de kust.
2. Figuera, j. 20000000000000000000. Wiskunde 1e. Gediversifieerd jaar. Co-bo edities.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Larson, r. 2010. Berekening van een variabele. 9NA. Editie. McGraw Hill.
5. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.