Groeiende functie hoe het te identificeren, voorbeelden, oefeningen

Jij hebt er een groeiende functie Wanneer de waarde van Y toeneemt als de X ook toeneemt, in tegenstelling tot de afnemende functies, waarin de waarde van en afneemt wanneer de X toeneemt.

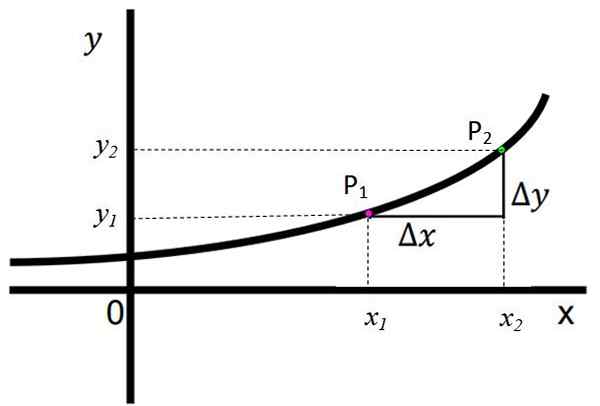
De volgende figuur toont een groeiende functie, en er wordt duidelijk opgemerkt dat bij het verplaatsen van links naar rechts op de X -as, de waarde van de respectieve coördinaat en, equivalent aan F (x), geleidelijk toeneemt. Er wordt gezegd dat als voor alles x₂ > x₁, Dan bestaat het en₂ > En₁.

Figuur 1. Een groeiende functie. Bron: f. Zapata.

De punten P₁ En P₂ Ze worden getoond, ze hebben respectievelijk coördinaten (x₁, En₁) en (x₂,En₂)). Ze zijn gedefinieerd:

Δy = y₂ -En₁

Δx = x₂ -X₁

In deze functie hebben zowel Δy als Δx een positief teken, wat betekent dat en₂ > En₁ en x₂ > x₁, respectievelijk. Dit is een duidelijk teken dat de functie effectief groeit.

Een goed voorbeeld van altijd de groeiende functie (toenemend monotoon) is het Neperiaanse logaritme van een reëel aantal. Hoe hoger het getal, hoe groter zijn logaritme.

[TOC]

Hoe u een groeiende functie kunt identificeren?

In een eenvoudige en continue functie zoals weergegeven in figuur 1, is het eenvoudig om te bepalen of de functie toeneemt of afneemt, op voorwaarde dat de grafiek beschikbaar is.

Meer complexe functies kunnen echter in sommige intervallen groeien en in andere afnemen. Daarom praten we over Groeiparen en afnemen van een functie.

In het netwerk zijn er gratis online graphics, zoals Geogebra, waarmee allerlei functies kunnen worden ingeprent. Met de grafiek is het eenvoudig om te bepalen of de functie altijd toeneemt, zoals f (x) = log x of dat het intervallen heeft waarin deze groeit en andere waarin deze afneemt en wat zijn.

Criterium van de eerste afgeleide

Overweeg een bepaald numeriek interval I, als het quotiënt tussen hoeveelheden Δy en Δx positief is, neemt de functie toe. En integendeel, als het negatief is, neemt de functie af.

Het kan u van dienst zijn: frequentiekans: concept, hoe het wordt berekend en voorbeelden

Je moet:

Δy / Δx> 0 → groeiende functie

Het feit dat Δy / Δx> 0 en de functie in een bepaald interval toeneemt, suggereert dat de eerste afgeleid van de functie, of liever het teken ervan, kan worden gebruikt als een criterium om te bepalen of de functie in feite in een bepaald interval of zelfs op een bepaald punt van uw domein.

Inderdaad, de eerste afgeleide wordt gedefinieerd als de helling van de curve elk punt:

Wat betekent dat Δx zo klein kan worden gedaan als je wilt. Als f '(x)> 0 voor een bepaalde waarde van x, bijvoorbeeld x = a, is de helling van de curve op dat punt f' (a) positief en zal de functie daar toenemen.

De volgende stelling biedt een criterium om te weten wanneer een functie in het interval groeit (a, b):

Stelling

Laat f (x) een afleidbare functie zijn in (a, b). Als f '(x)> 0, voor elke waarde van x behoort tot het genoemde interval, wordt gezegd dat f (x) groeit in (a, b).

De stelling wordt toegepast om erachter te komen in welke intervallen de functie groeit, volgens deze stappen:

Stap 1

Zoek de punten waarop f '(x) = 0, evenals die waarin f' (x) niet bestaat. Deze, geroepen kritieke punten, Dit zijn punten waar f '(x) van teken kan veranderen en daarom F (x) de mogelijkheid heeft om van groeien naar af te nemen of vice versa.

Stap 2

Zoek het teken van f '(x) voor willekeurige waarde in elk van de intervallen bepaald door de punten gevonden in stap 1.

Stap 3

Gebruik de stelling om te weten of de functie groeit of niet in elk interval.

Voorbeelden van groeiende functies

Er zijn functies met enkele groeiparen en andere afname, maar die hieronder worden getoond, groeien altijd.

Gewicht op basis van leeftijd

Het gewicht van de persoon sinds het werd geboren, totdat ongeveer de adolescentie beëindigt, is bijna altijd een groeiende functie van leeftijd. Baby's en kinderen groeien en ontwikkelen zich in de loop der jaren, en dan, wanneer ze volwassen worden, wordt verwacht dat de rest van hun leven een stabiel gewicht handhaaft, hoewel de ups en downs zeer frequent zijn.

Kan u van dienst zijn: verticale lijn

De logaritm -functie

De functies van reële variabele logaritme Neperian f (x) = ln x en decimale logaritm f (x) = log x groeien altijd.

De vierkantswortelfunctie van een reëel getal

Een andere functie die altijd groeit, is de vierkantswortelfunctie van een positief reëel getal:

y = √x

De gerelateerde functie en lineaire functie

De gerelateerde functie:

f (x) = mx + b

Het groeit wanneer de lijn een positieve helling is. Evenzo, identiteit en lineaire functies:

f (x) = x en f (x) = ax, met een> 0

Ze groeien in al hun domein.

De exponentiële functie

Een exponentiële functie zoals f (x) = e^X  En in het algemeen, de functie van de vorm:

f (x) = a^X, Met een> 1

Ze groeien in al hun domein.

De potentiële Impar -indexfunctie

De potentiële functies van oneven exponent, zoals deze:

• f (x) = x³
• g (x) = x⁵

Ze groeien altijd.

Opdrachten

Oefening 1

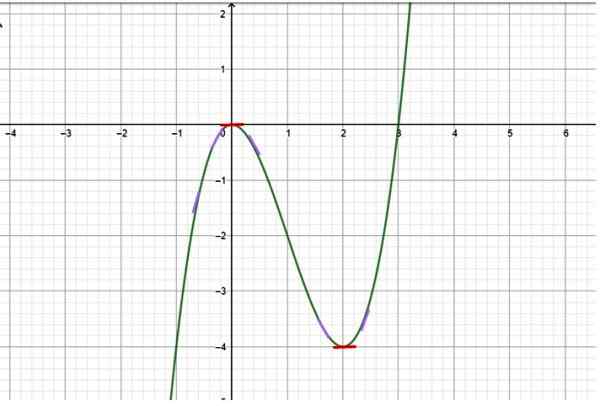
Bepaal in welke intervallen de functie weergegeven in de volgende grafiek neemt toe:

Figuur 2. Functie met groei en afname -intervallen. Bron: f. Zapata.

Oplossing

Naarmate de grafiek beschikbaar is, wordt uit de zorgvuldige observatie vastgesteld dat de functie het volgende gedrag heeft:

-Van x → -∞ tot x = 0 neemt de functie toe, omdat de waarden van Y steeds minder negatief worden. Kleine hellingssegmenten zijn paars getekend om de helling van de raaklijn op de curve op verschillende punten aan te geven (de helling van de raaklijn naar de curve is precies de eerste afgeleide).

Deze segmenten hebben een positieve helling, dus de stelling zorgt ervoor dat de functie in dit interval groeit.

-Maar bij x = 0 wordt de helling van de curve geannuleerd, wat wordt aangegeven met een klein horizontaal rood segment. Dit is een kritisch punt van de functie.

Kan je van dienst zijn: wat zijn wiskunde en waar zijn ze voor? 7 belangrijke toepassingen

Van daaruit begint de functie af te nemen, waarbij hij negatiever wordt, de waarden van en. Deze situatie gaat door tot x = 2, wat een ander kritisch punt is.

Vervolgens neemt in het interval van x = 0 tot x = 2 de functie af.

-Van x = 2 wordt de functie steeds minder negatief, totdat bij x = 3 de x -as kruist en elke keer positiever wordt. Daarom is dit een groei -interval.

Conclusie: de groei-intervallen zijn (-∞, 0) en (2, ∞+), terwijl het afname-interval (0,2) is.

Oefening 2

Bepaal de groeimiddelen van de volgende functie, door de criteria van de eerste afgeleide:

f (x) = x² - 2x

Oplossing

Volgens de hierboven aangegeven stappen wordt de eerste afgeleide berekend en is het gelijk aan 0 om de kritieke punten te vinden:

f '(x) = 2x -2

2x - 2 = 0

x = 1

Deze waarde bepaalt het bestaan ​​van de intervallen (-∞, 1) en (1, ∞+). Er worden twee willekeurige waarden gekozen die bij elk behoren:

-Voor x = 0, die tot (-∞, 1) behoort, moet u f '(0) = 2.0 - 2 = -2. Als het resultaat is negatief, neemt de functie in dit interval af.

-Voor x = 3, behorend tot (1, ∞+), is de eerste afgeleide f '(3) = 2 waard.3 - 2 = 4. Omdat het resultaat positief is, wordt geconcludeerd dat de functie in dit interval groeit.

De lezer kan de oorspronkelijke functie f (x) = x grafieken² - 2x op een online afbeelding om dit resultaat te bevestigen.

Referenties

1. Ayres, f. 20000000000000000000. Berekening. 5ed. MC Graw Hill.
2. Leithold, l. 1992. Berekening met analytische geometrie. Harla, s.NAAR.
3. Purcell, E. J., Varberg, D., & Rigdon, s. EN. (2007). Berekening. Mexico: Pearson Education.
4. Matemobile. Functies, groeien, afnemen en constant. Hersteld van: Matemovil.com
5. Eisen, b. Groeiende functies. Hersteld van: UniversOFormulas.com.
6. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.