Algemene formule kwadratische vergelijkingen, voorbeelden, oefeningen

De Algemene formule, die ook bekend staat als de oplosmiddel formule In sommige teksten wordt het gebruikt om tweedegraads vergelijkingen op te lossen: bijl² + bx + c = 0.

In hen naar, B En C Het zijn reële getallen, met de voorwaarde dat naar is anders dan 0, zijn X Het onbekende. Vervolgens presenteert de algemene formule de klaring van het onbekende door een uitdrukking die de waarden van naar, B En C als volgt:

Figuur 1. De algemene formule in de wiskunde wordt gebruikt om kwadratische vergelijkingen op te lossen. Bron: f. Zapata.

En via deze formule kunt u de oplossing vinden van elke tweede graad of kwadratische vergelijking, op voorwaarde dat deze oplossing bestaat.

Volgens historici was de algemene formule al bekend onder de oude Babylonische wiskunde. Het werd vervolgens overgedragen aan andere volkeren, zoals de Egyptenaren en de Grieken, door culturele beurzen.

De formule en zijn varianten zijn in Europa aangekomen dankzij de moslim wiskundigen die zich op het Iberische schiereiland vestigden. Ze hebben echter niet de algebraïsche notatie gebruikt die we momenteel gebruiken. Deze notatie is te wijten aan de Franse wiskundige en de 16e -eeuwse cryptografische expert Francois Viete.

[TOC]

Kwadratische vergelijkingen door de algemene formule

Laten we eens kijken hoe de algemene formule zich voordoet om de geldigheid ervan te verifiëren. Beginnend bij een algemene kwadratische vergelijking:

bijl² + bx + c = 0

Laten we enkele eenvoudige algebraïsche manipulaties in de praktijk brengen om de opruiming van het onbekende te bereiken. Er zijn verschillende manieren om dit mee te nemen, bijvoorbeeld het voltooien van vierkanten, zoals dan getoond.

Demonstratie van de algemene formule

We beginnen met het toevoegen van (-c) aan beide zijden van gelijkheid:

bijl² + Bx = - c

En nu wordt het vermenigvuldigd met 4A, altijd aan beide zijden van gelijkheid, om de uitdrukking niet te veranderen:

4e² X² + 4ab x = - 4ac

Het toevoegen van B²:

4e²⋅x² + 4ab⋅x + B² = - 4ac + B²

Het doel hiervan is om vierkanten aan de linkerkant van gelijkheid te voltooien, die het onbekende bevatten, op deze manier wordt de goedkeuring vergemakkelijkt. Dus:

Kan u van dienst zijn: divisors van 8: wat zijn en gemakkelijke uitleg

-De eerste termijn: 4e² X² Het is het perfecte vierkant van 2AX

-De laatste, die B is², Het is het perfecte vierkant van B.

-En de centrale term is het dubbele product van 2AX en B: 2⋅2AX⋅B = 4ABX

Daarom hebben we een vierkant binomiaal:

4e²⋅x² + 4ab⋅x + B² = (2AX + B)²

En we kunnen schrijven:

(2AX + B)² = - 4ac + B²

We zijn een stap verwijderd van het opruimen van het onbekende X:

En we verkrijgen al de algemene formule die we kennen:

Er zijn andere manieren om de kwadratische vergelijking te manipuleren en hetzelfde resultaat te verkrijgen.

Voorbeelden van het gebruik van de algemene formule

Om de algemene formule toe te passen, worden de waarden van A, B en C zorgvuldig bepaald en vervangen in de formule. Let op het symbool meer of minder in de teller; Dit geeft aan dat we twee mogelijkheden moeten overwegen met betrekking tot de operatie, één met het teken + en één met het bord -.

De kwadratische vergelijking kan de volgende oplossingen hebben, volgens de waarde van de sub-radicale hoeveelheid, bekend als discriminerend:

-Ja b² - 4ac> 0, de kwadratische vergelijking heeft twee echte en verschillende oplossingen.

-Wanneer B² - 4AC = 0, de vergelijking heeft een unieke oplossing, gegeven door:

x = -b/2a

-Eindelijk, als B² - 4AC < 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

Laten we eens kijken naar enkele voorbeelden waarin de algemene formule wordt toegepast, en merken op dat als een van de coëfficiënten die bij het onbekende hanteren niet lijkt, wordt begrepen dat het 1 waard is. En als de onafhankelijke term degene is die niet wordt gevonden, is het 0 waard.

- voorbeeld 1

Los de volgende kwadratische vergelijkingen op:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Antwoord op

We schrijven de coëfficiënten van elke term: a = 6, b = 11, c = -10 en vervangen de waarden in de algemene formule:

Kan u van dienst zijn: belastend

x = (-11 ± 19) /12

Het resultaat leidt tot de volgende twee echte oplossingen:

X₁ = (-11 + 19)/12 = 8/12 = 2/3

X₂ = (-11 -19)/12 = -5/2

Antwoord B

Nogmaals, de coëfficiënten worden bepaald: a = 3, b = -5 en c = -1. Door de formule te vervangen:

In tegenstelling tot het vorige geval is de vierkantswortel van 37 geen geheel getal, maar we kunnen ook de twee oplossingen verhogen en de wortel verlaten of de overeenkomstige decimale waarde vinden met behulp van de rekenmachine:

X₁ = (-5 + √37)/6 ≈ 0.18

X₂ = (-5 - √37)/6 ≈ - 1.85

- Voorbeeld 2

Los de tweede graad vergelijking x op² - 4x +13 = 0.

Antwoord

Zoals altijd identificeren we de waarden van de coëfficiënten en vervangen we de algemene formule: a = 1, b = - 4, c = 13. Dit leidt tot:

We hebben een negatieve wortel, daarom zijn de oplossingen van deze vergelijking complexe getallen. De wortel kan worden uitgedrukt in termen van Je, de Denkbeeldige eenheid:

√ (36i²) = 6i

Sinds ik² = -1, daarom zijn de complexe oplossingen:

X₁ = (4 + 6i)/2 = 2 + 3i

X₂ = (4 - 6i)/2 = 2 - 3i

Oefening opgelost

Een trap van 10 m lange trap ligt tegen een verticale muur, met de voet 6 m van die muur. De trap glijdt en de voet is 3 m meer gescheiden van de basis.

Zoek de verticale afstand die door de bovenkant van de trap loopt.

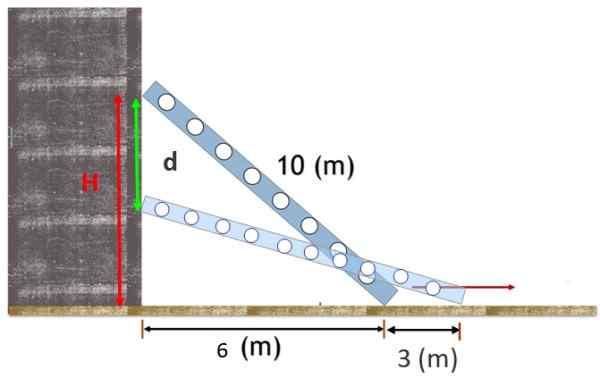Figuur 2. Een trap die op een muur wordt ondersteund een beetje en de bovenste stop beweegt verticaal een afstand D af. Bron: f. Zapata.

Oplossing

Om de verticale afstand te vinden die over de bovenkant van de trap schuift, moet u de positie vinden waarin deze oorspronkelijk met betrekking tot de grond was. We kunnen het doen met de stelling van Pythagoras, omdat de gevormde figuur die van een rechterdriehoek is:

H = (10² - 6²)) ^½ = 8 m

Zodra de trap glijdt, beweegt een afstand D, Meet omdat de bovenkant 8 m hoog was, totdat deze zijn nieuwe positie bereikte, op (H-D) meters boven de grond. Het onbekende om te wissen is D.

Kan u van dienst zijn: Gecumuleerde frequentie: formule, berekening, verdeling, voorbeelden

Om het te vinden, stellen we een nieuwe rechthoekige driehoek voor, die is gevormd nadat de ladder een beetje is uitgegleden. Deze driehoek heeft nog steeds hypotenusa gelijk aan 10 m en de parallelle cateto is nu 6m + 3m = 9 m, daarom:

(H-D)² = 10² - 9² = 100 - 81 = 19

We vervangen h = 8m, eerder berekend:

(8-D)² = 19

De vergelijking kan op verschillende manieren worden opgelost, inclusief het gebruik van de algemene formule, die we hieronder met deze stappen zullen laten zien:

Stap 1

Ontwikkel het opmerkelijke links van links:

64 -16D + D² = 19

Stap 2

Stel de tweede graad vergelijking in voor onbekende d:

D² - 16d + 45 = 0

Stap 3

-De coëfficiënten zijn: A = 1, B = -16 en C = 45, we vervangen ze in de algemene formule:

De oplossingen van de vergelijking zijn:

D₁ = (16 + √76)/2 ≈ 12.36 m

D₂ = (16 - √76)/2 ≈ 3.64 m

Stap 4

De verkregen oplossingen worden geanalyseerd: de eerste is niet fysiek logisch, omdat het niet mogelijk is voor de ladder om 12 te compileren.36 m, als oorspronkelijk de stop 8 m hoog op de grond was.

Daarom is het juiste antwoord de tweede oplossing: de bovenkant van de trap slipt d = 3.64 m.

Kan de lezer het probleem oplossen door een andere methode toe te passen?

Referenties

1. Baldor. 1977. Elementaire algebra. Venezolaanse culturele edities.
2. Hoffman, J. Selectie van wiskundeproblemen. Deel 2.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
5. Zill, D. 1984. Algebra en trigonometrie. McGraw Hill.