Absolute frequentieformule, berekening, verdeling, voorbeeld

De Absolute frecuency Het wordt gedefinieerd als het aantal keren dat dezelfde gegevens worden herhaald binnen de reeks observaties van een numerieke variabele. De som van alle absolute frequenties is gelijk aan het in totaal de gegevens.

Wanneer er veel waarden van een statistische variabele zijn, is het handig om ze goed te organiseren om informatie over hun gedrag te extraheren. Dergelijke informatie wordt gegeven door centrale tendensmaatregelen en dispersiemaatregelen.

Figuur 1. De absolute frequentie van een statistische observatie is de sleutel tot het vinden van de trend die de gegevensset volgt

In de berekeningen van deze maatregelen worden de gegevens weergegeven door de frequentie waarmee ze in alle waarnemingen verschijnen.

Het volgende voorbeeld laat zien hoe het onthullen van de absolute frequentie van elke gegevens is. Tijdens de eerste helft van mei waren dit de maten van beste cocktailkostuums, van een goed bekend dameskledingmagazijn:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Hoeveel jurken worden in een bepaalde grootte verkocht, bijvoorbeeld maat 10? Eigenaren zijn geïnteresseerd in het weten om bestellingen te geven.

Het bestellen van de gegevens is gemakkelijker te tellen, er zijn in totaal exact 30 observaties, dan geordend van de kleinste tot de hoogste zijn als volgt:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

En nu is het duidelijk dat maat 10 6 keer wordt herhaald, daarom is de absolute frequentie gelijk aan 6. Dezelfde procedure wordt uitgevoerd om de absolute frequentie van de resterende maten te achterhalen.

[TOC]

Formules

De absolute frequentie, aangeduid als f_Je, Het is gelijk aan het aantal keren als een bepaalde X -waarde_Je bevindt zich binnen de groep van observaties.

Ervan uitgaande dat de totale waarnemingen van N -waarden zijn, moet de som van alle absolute frequenties gelijk zijn aan dit getal:

Kan u van dienst zijn: papomudas

∑f_Je = f₁ + F₂ + F₃ +… F_N = N

Andere frequenties

Als elke waarde van f_Je Het wordt gedeeld door het totale aantal gegevens n, u hebt de relatieve frequentie F_R van waarde x_Je:

F_R = f_Je / N

Relatieve frequenties zijn waarden tussen 0 en 1, omdat n altijd groter is dan elke f_Je, Maar de som moet gelijk zijn aan 1.

Vermenigvuldigen met 100 tot elke waarde van f_R jij hebt de Relatieve procentuele frequentie, wiens som 100%is:

Relatieve procentuele frequentie = (f_Je / N) x 100%

Het is ook belangrijk opgebouwde frequentie F_Je Tot een bepaalde observatie is dit de som van alle absolute frequenties totdat deze observatie inclusief observatie:

F_Je = f₁ + F₂ + F₃ +… F_Je

Als de geaccumuleerde frequentie wordt gedeeld door het totale aantal gegevens n, heeft u de verzamelde relatieve frequentie, die vermenigvuldigde per 100 resulteert in de Gecumuleerd relatief frequentiepercentage.

Hoe u de absolute frequentie kunt krijgen?

Om de absolute frequentie te vinden van een bepaalde waarde die tot een gegevensset behoort, zijn ze allemaal van het minst tot de grootste georganiseerd en wordt de waarde geteld.

In het voorbeeld van de maten van de jurken is de absolute frequentie van maat 4 3 jurken, dat wil zeggen f₁ = 3. Voor maat 6 werden 4 jurken verkocht: F₂ = 4. In maat 8 4 -jurken werden ook verkocht, f₃ = 4 enzovoort.

Tabel

De totale resultaten kunnen worden weergegeven in een tabel die de absolute frequenties van elk toont:

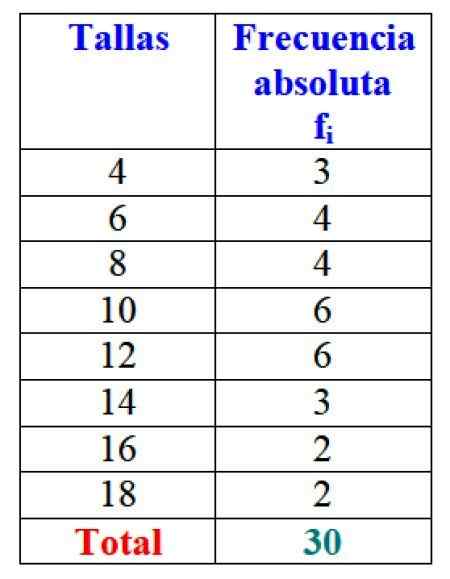Figuur 2. Tabel die de variabele "verkochte verkoop" en de respectieve absolute frequenties weergeeft. Bron: f. Zapata.

Het is duidelijk voordelig om de informatie te bestellen en er toegang toe te hebben, in plaats van te werken met losse gegevens.

Belangrijk: Merk op dat door alle waarden van kolom F toe te voegen_Je  Het totale aantal gegevens wordt altijd verkregen. Zo niet, dan moet de boekhouding worden beoordeeld, omdat er een fout is.

Uitgebreide frequentietabel

De vorige tabel kan worden uitgebreid door de andere soorten frequentie in opeenvolgende kolommen aan de rechterkant toe te voegen:

Kan u van dienst zijn: HOMOCEDASTICITEIT: Wat is belangrijk en voorbeelden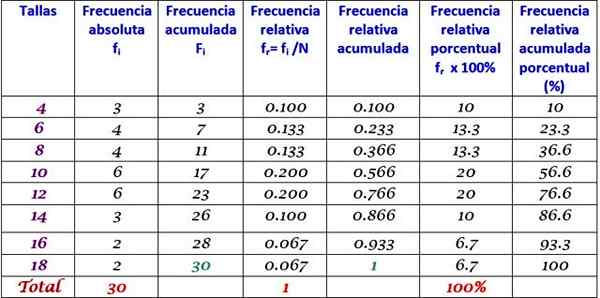

Frequentieverdeling

Frequentieverdeling is het resultaat van het organiseren van gegevens in termen van hun frequenties. Bij het werken met veel gegevens is het handig om ze te groeperen in categorieën, intervallen of klassen, elk met hun respectieve frequenties: absoluut, relatief, geaccumuleerd en percentage.

Het doel om ze te doen is om gemakkelijker toegang te krijgen tot de informatie die de gegevens bevatten, en ze goed te interpreteren, wat niet mogelijk is wanneer ze zonder bestelling worden gepresenteerd.

In het voorbeeld van de maten zijn de gegevens niet gegroepeerd, omdat ze niet te veel maten zijn en gemakkelijk kunnen worden gemanipuleerd en geteld. Kwalitatieve variabelen kunnen ook op deze manier worden gewerkt, maar als de gegevens heel talrijk zijn, werken ze beter in de klassen.

Frequentieverdeling voor gegroepeerde gegevens

Om de gegevens in klassen van gelijke grootte te groeperen, moet het volgende worden overwogen:

-Grootte, breedte of klassenamplitude: Het is het verschil tussen de grootste waarde van de klasse en de minderjarige.

Klasgrootte wordt bepaald door het bereik R te delen door het aantal te overwegen klassen. Het bereik is het verschil tussen de maximale waarde van de gegevens en de minderjarige, zoals deze:

Klasgrootte = bereik / aantal klassen.

-Klasse limiet: Interval dat van de ondergrens naar de bovengrens van de klasse gaat.

-Klasmerk: Het is het middelpunt van het interval, dat als representatief voor de klasse wordt beschouwd. Het wordt berekend met de semi -beperking van de bovengrens en de ondergrens van de klasse.

-Aantal klassen: Sturges -formule kan worden gebruikt:

Klassen = 1 + 3.322 log n

Waar n het aantal klassen is. Zoals meestal een decimaal nummer is, is het volgende afgerond.

Voorbeeld

Een grote fabrieksmachine is buiten gebruik, omdat het terugkerende mislukkingen heeft. De opeenvolgende perioden van inactiviteit in minuten, van genoemde machine, worden hieronder opgenomen, met in totaal 100 gegevens:

Het kan u van dienst zijn: frequentiekans: concept, hoe het wordt berekend en voorbeelden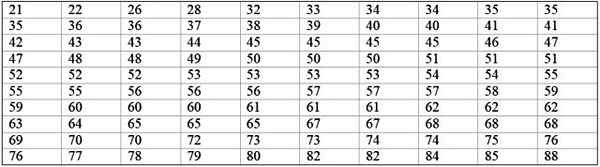

Eerst wordt het aantal klassen bepaald:

Klassen = 1 + 3,322 log n = 1 + 3.32 Log 100 = 7.64 ≈ 8

Klasse grootte = bereik / aantal klassen = (88-21) / 8 = 8.375

Het is ook een decimaal nummer, dus het duurt 9 als klassengrootte.

Het klassenmerk is het gemiddelde tussen de bovenste en ondergrens van de klasse, bijvoorbeeld voor klasse [20-29) Er is een kenmerk van:

Class Brand = (29 + 20) / 2 = 24.5

Ga op dezelfde manier verder om de klassenmerken van de resterende intervallen te vinden.

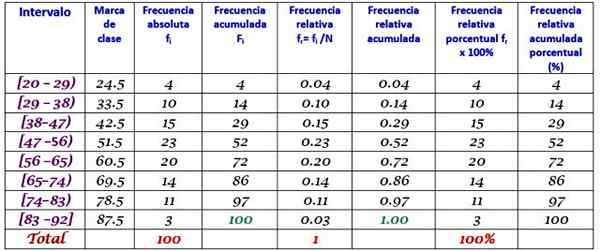
Oefening opgelost

40 jonge mensen gaven aan dat de tijd in minuten die afgelopen zondag op internet voorbijgingen, de volgende was, in toenemende mate besteld:

0; 12; twintig; 35; 35; 38; 40; Vier vijf; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

Er wordt gevraagd om de frequentieverdeling van deze gegevens te bouwen.

Oplossing

De rang R van de set van N = 40 -gegevens is:

R = 220 - 0 = 220

De toepassing van de Sturges -formule om het aantal klassen te bepalen levert het volgende resultaat op:

Klassen = 1 + 3,322 log n = 1 + 3.32 log 40 = 6.3

Zoals een decimaal is, is het directe geheel 7, daarom zijn de gegevens gegroepeerd in 7 klassen. Elke klasse heeft een breedte van:

Klasgrootte = bereik / aantal klassen = 220/7 = 31.4

Een hechte en ronde waarde is 35, daarom wordt een klassenbreedte van 35 gekozen.

Klassenmarkeringen worden berekend met het gemiddelde van de bovenste en ondergrens van elk interval, bijvoorbeeld voor het interval [0,35):

Class Brand = (0+35)/2 = 17.5

We gaan op dezelfde manier door met de resterende klassen.

Ten slotte worden de frequenties berekend volgens de hierboven beschreven procedure, wat resulteert in de volgende verdeling:

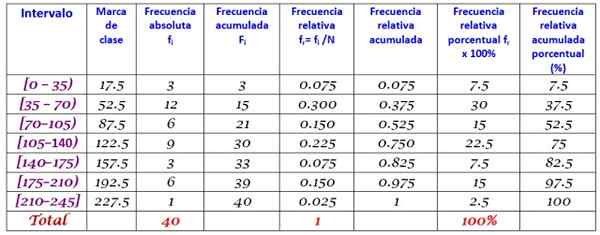
Referenties

1. Berenson, m. 1985. Statistieken voor administratie en economie. Inter -American S.NAAR.
2. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
3. Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.
4. Spiegel, m. 2009. Statistieken. Schaum -serie. 4 TA. Editie. McGraw Hill.
5. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.