Inferentiële statistiekengeschiedenis, kenmerken, waarvoor is het voor voorbeelden

De Inferentiële statistieken of deductieve statistieken is er een die de kenmerken van een populatie afleidt uit monsters die eruit zijn geëxtraheerd, via een reeks analysetechnieken. Met de verkregen informatie worden modellen uitgewerkt die vervolgens voorspellingen toestaan ​​over het gedrag van deze populatie.

Daarom zijn inferentiële statistieken de belangrijkste wetenschap geworden die onderhoud en instrumenten aanbiedt die talloze disciplines vereisen, bij het nemen van beslissingen.

Natuurkunde, scheikunde, biologie, engineering en sociale wetenschappen, profiteren voortdurend van deze tools wanneer ze hun modellen maken en experimenten ontwerpen en implementeren.

[TOC]

Korte geschiedenis van inferentiële statistieken

Statistieken zijn in de oudheid ontstaan ​​vanwege de noodzaak van mensen om dingen te organiseren en middelen te optimaliseren. Vóór de uitvinding van het schrijven werden records van het aantal mensen en vee uitgevoerd, via symbolen die in steen werden opgenomen.

Later lieten Chinese, Babylonische en Egyptische heersers gegevens over over de hoeveelheid gewassen en het aantal inwoners, geregistreerd op kleitabletten, kolommen en monumenten.

Romeinse rijk

Toen Rome zijn domein in de Middellandse Zee uitoefende, was het gebruikelijk dat de autoriteiten om de vijf jaar tellingen uit te voeren. In feite komt het woord "statistisch" uit het Italiaanse woord statista, Wat betekent het om uit te drukken.

Tegelijkertijd brachten de grote pre -Columbiaanse rijken in Amerika ook soortgelijke records mee.

Middeleeuwen

Tijdens de middeleeuwen registreerden de regeringen van Europa, evenals de kerk, het eigendom van de aarde. Toen deden ze hetzelfde met geboorten, dopen, huwelijken en sterfgevallen.

Moderne tijd

De Engelse statistiek John Graunt (1620-1674) was de eerste die voorspellingen deed op basis van dergelijke lijsten, zoals hoeveel mensen konden sterven aan bepaalde ziekten en het geschatte deel van de geboorten van vrouwen en mannen. Daarom wordt de vader van demografie overwogen.

Hedendaagse leeftijd

Later, met de komst van de waarschijnlijkheidstheorie, waren statistieken niet meer een verzameling organisatietechnieken en bereikten ze een onverwachte scope als een voorspellende wetenschap.

Aldus konden experts in staat zijn.

Kenmerken

Hieronder hebben we de meest relevante kenmerken van deze statistiekentak:

- Inferentiële statistieken bestuderen een populatie die hieruit een representatieve steekproef haalt.

- De monsterselectie wordt uitgevoerd via verschillende procedures, de meest geschikte zijn degenen die de componenten willekeurig kiezen. Aldus heeft elk element van de populatie dezelfde kans om gekozen te worden en daarmee worden ongewenste vooroordelen vermeden.

Kan u van dienst zijn: hoe u kunt converteren vanaf km/h a m/s? Opgeloste oefeningen

- Om de verzamelde informatie te organiseren, maakt het gebruik van beschrijvende statistieken.

- Op de steekproef worden statistische variabelen berekend die dienen om de eigenschappen van de bevolking te schatten.

- Inferentiële of deductieve statistieken maken gebruik van de waarschijnlijkhedenstheorie om willekeurige gebeurtenissen te bestuderen, dat wil zeggen degenen die toevallig optreden. Elke gebeurtenis krijgt een bepaalde kans op voorkomen.

- Bouw hypothesen -suposities op over de parameters van de populatie en contrasteren ze, om te weten of ze al dan niet correct zijn en berekent ook het vertrouwensniveau van de respons, dat wil zeggen dat het een foutmarge biedt. De eerste procedure wordt genoemd Hypothesetests, Terwijl de foutenmarge de Betrouwbaarheidsinterval.

Wat is beschrijvende statistieken voor? Toepassingen

Inferentiële statistieken: essentieel bij het nemen van beslissingen en kwaliteitscontrole

Studie in zijn geheel kan een bevolking veel middelen eisen in geld, tijd en moeite. Het verdient de voorkeur om representatieve monsters te nemen die veel beter beheersbaar zijn, gegevens door hen verzamelen en hypothesen of veronderstellingen over steekproefgedrag creëren.

Zodra de hypothesen zijn vastgesteld en hun geldigheid is contrast.

Ze helpen ook om modellen van die populatie te maken, om toekomstige projecties te maken. Daarom is inferentiële statistieken een zeer nuttige wetenschap voor:

Sociologie en demografische studies

Dit zijn ideale applicatievelden, omdat statistische technieken van toepassing zijn op het idee om verschillende modellen van menselijk gedrag op te zetten. Iets dat a priori vrij ingewikkeld is, omdat talloze variabelen ingrijpen.

In de politiek wordt er veel gebruikt in de verkiezingstijd om de neiging tot kiezers te kennen, op deze manier ontwerpen de strategieën van de partijen.

Engineering

Inferentiële statistiekenmethoden worden veel gebruikt in engineering, de belangrijkste toepassingen zijn de kwaliteitscontrole en verwerkten optimalisatie, bijvoorbeeld het verbeteren van de tijden bij het uitvoeren van taken, evenals bij het voorkomen van beroepsgevallen.

Economie en bedrijfskunde 

Met de deductieve methoden kunnen projecties worden uitgevoerd over de werking van een bedrijf, het verwachte verkoopniveau en hulp bij het nemen van beslissingen.

Uw technieken kunnen bijvoorbeeld worden gebruikt om de reactie van kopers op een nieuw product te schatten, dicht bij de lancering van de markt.

Het dient ook om te evalueren wat de wijzigingen in de verbruiksgewoonten van mensen zijn, gezien belangrijke gebeurtenissen, zoals de covid -epidemie.

Voorbeelden van inferentiële statistieken

voorbeeld 1

Een eenvoudig deductief statistisch probleem is als volgt: een wiskundeleraar heeft de leiding over 5 secties elementaire algebra in een universiteit en besluit de gemiddelde aantekeningen van een enkele van hun secties te gebruiken om het gemiddelde van allemaal te schatten.

Kan u van dienst zijn: bij benadering meting van amorfe figuren: voorbeeld en oefeningMaar grote populatie kan worden bestudeerd via een representatieve steekproef. Bron: Pixabay.

Een andere mogelijkheid is om een ​​steekproef van elke sectie te nemen, de kenmerken ervan te bestuderen en de resultaten uit te breiden naar alle secties.

Voorbeeld 2

De manager van een kledingwinkel voor dames wil weten hoeveel een bepaalde blouse zal worden verkocht tijdens het zomerseizoen. Om dit te doen, analyseer je kledingverkoop tijdens de eerste twee weken van het seizoen en bepaal zo de trend.

Basisconcepten in inferentiële statistieken

Er zijn verschillende belangrijke concepten, waaronder die van de waarschijnlijkheidstheorie, die noodzakelijk zijn om alle reikwijdte van deze technieken duidelijk te begrijpen. Sommigen, als een populatie en steekproef, hebben we al in de tekst vermeld.

Evenement

Een gebeurtenis of gebeurtenis is iets dat gebeurt, en dat kan verschillende resultaten hebben. Een gebeurtenisvoorbeeld kan zijn om een ​​valuta te lanceren en er zijn twee mogelijke resultaten: gezicht of zegel.

Voorbeeldruimte

Het is de set van alle mogelijke resultaten van een evenement.

Bevolking en steekproef

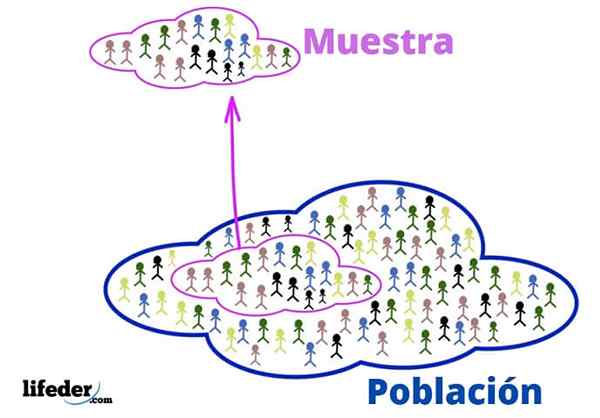Bevolking en steekproef

De bevolking is het universum om te studeren. Ze gaan niet noodzakelijkerwijs over levende mensen of wezens, omdat de bevolking in statistieken kan bestaan ​​uit objecten of ideeën.

Van zijn kant is de steekproef een subset van de bevolking, er zorgvuldig uit geëxtraheerd omdat hij representatief is.

Bemonstering

Het is de set technieken waardoor een steekproef is geselecteerd uit een bepaalde populatie. Bemonstering kan willekeurig zijn als probabilistische methoden worden gebruikt om de steekproef te kiezen, of niet probabilistisch, als de analist een eigen selectiecriterium heeft, volgens hun ervaring.

Statistische variabelen

Set van waarden die de kenmerken van de populatie kunnen hebben. Ze zijn op verschillende manieren geclassificeerd, bijvoorbeeld ze kunnen discreet of continu zijn. Volgens hun aard kunnen ze ook kwalitatief of kwantitatief zijn.

Waarschijnlijkheidsverdelingen

Waarschijnlijkheidsfuncties die het gedrag beschrijven van een groot aantal systemen en situaties die in de natuur worden waargenomen. De bekendste zijn Gaussiaanse distributie of Gauss Bell en Binomiale verdeling.

Parameters en statistieken 

De theorie van de schatting stelt vast dat er een verband bestaat tussen de waarden van de bevolking en die van de steekproef die uit die populatie is genomen. De parameters Ze zijn de kenmerken van de populatie die we niet kennen, maar we willen schatten: bijvoorbeeld het gemiddelde en de standaardafwijking.

Van zijn kant, de statistisch zijn de kenmerken van het monster, bijvoorbeeld de gemiddelde en standaardafwijking.

Stel bijvoorbeeld dat de bevolking uit alle jongeren bestaat tussen 17 en 30 jaar van een gemeenschap, en het is gewenst om het aandeel te kennen van degenen die momenteel in het hoger onderwijs zijn. Dit zou de te bepalen populatieparameter zijn.

Kan u van dienst zijn: lineaire interpolatie

Om het te schatten, wordt een willekeurige steekproef van 50 jongeren geselecteerd en wordt het aandeel van hen gestudeerd aan een universiteit of instituut voor hoger onderwijs berekend. Dit aandeel is de statistiek.

Als de studie wordt uitgevoerd, wordt vastgesteld dat 63 % van de 50 jongeren hoger studeren, dit is de geschatte populatie, gemaakt van de steekproef.

Dit is slechts een voorbeeld van wat inferentiële statistieken kunnen doen. Het staat bekend als schatting, maar er zijn ook technieken om statistische variabelen te voorspellen, en om beslissingen te nemen.

Statistische hypothese

Het is een vermoeden dat wordt gedaan met betrekking tot de waarde van het gemiddelde en de standaardafwijking van een kenmerk van de bevolking. Tenzij de bevolking volledig wordt onderzocht, zijn dit onbekende waarden.

Hypothesetests

Zijn de veronderstellingen over de populatieparameters geldig? Om het te weten, is het geverifieerd of de resultaten van de steekproef hen ondersteunen of niet, dus het is noodzakelijk om hypothese -tests te ontwerpen.

Dit zijn de algemene stappen om er een uit te voeren:

Stap 1

Identificeer het type verdeling dat de bevolking naar verwachting zal volgen.

Stap 2

Hef twee hypothesen op, aangeduid als h_of en h₁. De eerste is de nulhypothese waarin we aannemen dat de parameter een bepaalde waarde heeft. De tweede is De alternatieve hypothese wat een andere waarde is dan de nulhypothese. Als dit wordt afgewezen, wordt de alternatieve hypothese geaccepteerd.

Stap 3

Stel een acceptabele marge in voor het verschil tussen de parameter en de statistiek. Ze zullen zelden identiek zijn, hoewel van hen wordt verwacht dat ze heel dichtbij zijn.

Stap 4

Stel een criterium voor om de nulhypothese te accepteren of af te wijzen. Hiervoor wordt een teststatistiek gebruikt die het gemiddelde kan zijn. Als de gemiddelde waarde binnen bepaalde limieten valt, wordt de nulhypothese geaccepteerd, anders wordt deze afgewezen.

Stap 5

Als laatste stap wordt besloten of de nulhypothese al dan niet wordt geaccepteerd.

Thema's van belangstelling

Statistiektakken.

Statistische variabelen.

Bevolking en steekproef.

Beschrijvende statistieken.

Referenties

1. Berenson, m. 1985.Statistieken voor administratie en economie, concepten en toepassingen. Inter -Amerikaans redactioneel.
2. Canavos, G. 1988. Waarschijnlijkheid en statistieken: toepassingen en methoden. McGraw Hill.
3. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Cengage leren.
4. Statistiekengeschiedenis. Hersteld van: Eumed.netto.
5. Ibañez, P. 2010. Wiskunde II. Competentiebenadering. Cengage leren.
6. Levin, r. 1981. Statistieken voor beheerders. Prentice Hall.
7. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.