Bemonsteringsfoutformules en -vergelijkingen, berekening, voorbeelden
- 1268
- 208
- Dr. Rickey Hudson
Hij bemonsteringsfout of monsterfout In statistieken is het het verschil tussen de gemiddelde waarde van een steekproef ten opzichte van de gemiddelde waarde van de totale populatie. Om het idee te illustreren, laten we ons voorstellen dat de totale bevolking van een stad een miljoen is, van waaruit u de gemiddelde schoenen wilt, waarvoor duizend mensen willekeurig worden genomen.
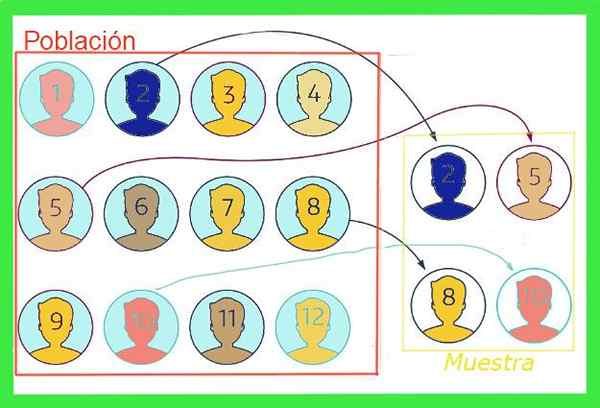
De gemiddelde grootte die voortvloeit uit de steekproef zal niet noodzakelijkerwijs samenvallen met die van de totale populatie, hoewel als de steekproef niet bevooroordeeld is, moet de waarde dichtbij zijn. Dit verschil tussen de gemiddelde waarde van de steekproef en die van de totale populatie is de steekproeffout.
 Figuur 1. Aangezien de steekproef een subset is van de totale populatie, heeft het gemiddelde van de steekproef een foutmarge. Bron: f. Zapata.
Figuur 1. Aangezien de steekproef een subset is van de totale populatie, heeft het gemiddelde van de steekproef een foutmarge. Bron: f. Zapata. Over het algemeen is de gemiddelde waarde van de totale populatie onbekend, maar er zijn technieken om een dergelijke fouten en formules te verminderen om de Monsterfoutmarge Dat zal in dit artikel worden getoond.
[TOC]
Formules en vergelijkingen
Laten we in het geval dat u de gemiddelde waarde van een bepaalde meetbare functie wilt weten X In een populatie van grootte N, maar hoe N Het is een groot aantal is niet haalbaar om de totale bevolking te bestuderen, dus gaan we verder met het nemen van een Aleatory sample van grootte N<
De gemiddelde waarde van de steekproef wordt aangegeven door en de gemiddelde waarde van de totale bevolking geeft deze aan voor de Griekse brief μ (er staat MU of MIU)).
Stel dat ze zijn genomen M Totale bevolkingsmonsters N, Alle gelijke grootte N Met gemiddelde waarden
Deze gemiddelde waarden zullen niet identiek aan elkaar zijn en zullen allemaal rond de gemiddelde populatiewaarde zijn μ. Hij Monsterfoutmarge e geeft de verwachte scheiding aan van de gemiddelde waarden ten opzichte van de Gemiddelde populatiewaarde μ Binnen een bepaald percentage genaamd de Vertrouwensniveau γ ((Gamma)).
Kan u van dienst zijn: additief inverseHij Standaardfoutmarge ε van het size monster N is:
ε = σ/√n
waar σ is de standaardafwijking (De vierkantswortel van de variantie), die wordt berekend door de volgende formule:
σ = √ [(x -)2/(N - 1)]
De betekenis van Standaardfoutmarge ε is de volgende:
Hij middelwaarde verkregen door het size monster N wordt begrepen in de interval ( - ε, + ε) met een betrouwbaarheidsniveau 68,3%.
Hoe de steekproeffout te berekenen
In de vorige sectie werd de formule gegeven om de foutenbereik standaard van een steekproef van N, waarbij het standaardwoord aangeeft dat het een foutenmarge is met 68% vertrouwen.
Dit geeft aan dat als veel monsters van dezelfde grootte zijn genomen N, 68% van hen zal gemiddelde waarden in het bereik geven [ - ε, + ε].
Er is een eenvoudige regel, de naam van de Regel 68-95-99.7 waarmee we de marge van kunnen vinden van Voorbeeldfout e Voor betrouwbaarheidsniveaus van 68%, 95% En 99,7% Gemakkelijk, omdat deze marge 1⋅ isε, 2⋅ε en 3⋅ε respectievelijk.
Voor een betrouwbaarheidsniveau γ
Als hij Vertrouwensniveau γ Het is geen van de bovenstaande, dus de bemonsteringsfout is de standaardafwijking σ vermenigvuldigd met de factor Zy, die wordt verkregen via de volgende procedure:
1.- Eerst de significantieniveau α waaruit wordt berekend Vertrouwensniveau γ Door de volgende relatie: α = 1 - γ
Kan u van dienst zijn: Bayes Stelling2.- Dan moet je de waarde berekenen 1 - α/2 = (1 + γ)/2, die overeenkomt met de normale frequentie die is verzameld tussen -∞ en Zy, In een normale of Gaussiaanse verdeling getypeerd F (z), waarvan de definitie te zien is in figuur 2.
3.- De vergelijking is opgelost F (zy) = 1 - α/2 Via de normale distributietabellen (verzameld) F, o Via een computerapplicatie die de typeerde omgekeerde Gaussiaanse functie heeft F-1.
In het laatste geval heb je:
Zy = g-1(1 - α/2).
4.- Ten slotte wordt deze formule voor de bemonsteringsfout met een betrouwbaarheidsniveau toegepast γ:
E = zy⋅(σ/√n)
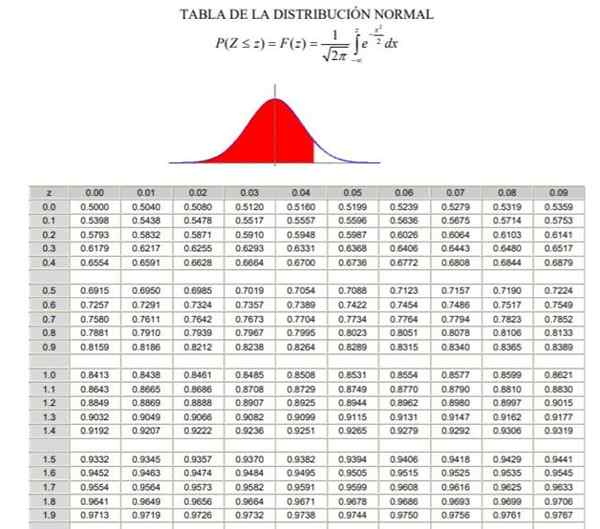 Figuur 2. Normale distributietabel. Bron: Wikimedia Commons.
Figuur 2. Normale distributietabel. Bron: Wikimedia Commons. Voorbeelden
- voorbeeld 1
Bereken de Standaard foutmarge Op het gemiddelde gewicht van een monster van 100 pasgeborenen. De berekening van het gemiddelde gewicht was = 3.100 kg met een standaardafwijking σ = 1500 kg.
Oplossing
Hij Standaard foutmarge is ε = σ/√n = (1.500 kg)/√100 = 0,15 kg. Wat betekent dat met deze gegevens kan worden afgeleid dat het gewicht van 68% van de pasgeborenen tussen 2.950 kg en 3 ligt.25 kg.
- Voorbeeld 2
Bepalen de marge van monsterfout en en het gewichtsbereik van 100 pasgeborenen met een betrouwbaarheidsniveau van 95% als het gemiddelde gewicht 3.100 kg is met standaardafwijking σ = 1500 kg.
Oplossing
Als de Regel 68; 95; 99.7 → 1⋅ε; 2⋅ε; 3⋅ε, Je hebt:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
Met andere woorden, 95% van de pasgeborenen zal peso hebben tussen 2.800 kg en 3.400 kg.
- Voorbeeld 3
Bepaal het pesosbereik van pasgeborenen van voorbeeld 1 met een betrouwbaarheidsmarge van 99,7%.
Kan u van dienst zijn: rhomboid: kenmerken, hoe u de perimeter en het gebied kunt verwijderenOplossing
De steekproeffout met 99,7% vertrouwen is 3 σ/√n, Dat voor ons voorbeeld is E = 3 *0,15 kg = 0,45 kg. Vanaf hier wordt afgeleid dat 99,7% van de pasgeborenen pesos zal hebben tussen 2.650 kg en 3.550 kg.
- Voorbeeld 4
Bepaal de factor Zy Voor een betrouwbaarheidsniveau van 75%. Bepaal de bemonsteringsfoutmarge met dit niveau van betrouwbaarheid voor de case die is verhoogd in Voorbeeld 1.
Oplossing
Hij betrouwbaarheidsniveau is γ = 75% = 0,75 die betrekking heeft op de mate van belang α door de relatie γ= (1 - α), zodat het significantieniveau is α = 1 - 0,75 = 0,25.
Dit betekent dat de opgebouwde normale waarschijnlijkheid tussen -∞ en Zy is:
P (z ≤ Zy ) = 1 - 0,125 = 0,875
Wat overeenkomt met een waarde Zy van 1.1503, zoals getoond in figuur 3.
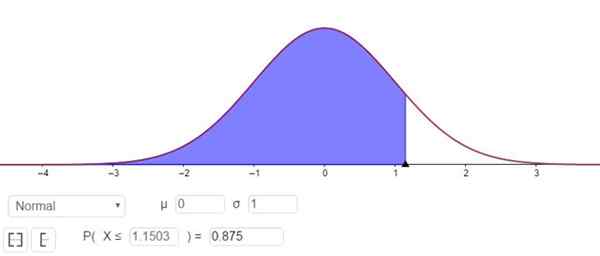 figuur 3. Bepaling van de Zy -factor die overeenkomt met een betrouwbaarheidsniveau van 75%. Bron: f. Zapata door Geogebra.
figuur 3. Bepaling van de Zy -factor die overeenkomt met een betrouwbaarheidsniveau van 75%. Bron: f. Zapata door Geogebra. Met andere woorden, de steekproeffout is E = zy⋅(σ/√n)= 1.15⋅(σ/√n).
Wanneer toegepast op voorbeeld 1 -gegevens, geeft dit een fout van:
E = 1,15*0,15 kg = 0,17 kg
Met een betrouwbaarheidsniveau van 75%.
- Oefening 5
Wat is het niveau van vertrouwen als Zα/2 = 2.4 ?
Oplossing
P (z ≤ zα/2 ) = 1 - α/2
P (z ≤ 2.4) = 1 - α/2 = 0.9918 → α/2 = 1 - 0.9918 = 0.0082 → α = 0,0164
Het significantieniveau is:
α = 0,0164 = 1,64%
En ten slotte blijft het vertrouwensniveau bestaan:
1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%
Referenties
- Canavos, G. 1988. Waarschijnlijkheid en statistieken: toepassingen en methoden. McGraw Hill.
- Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
- Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.
- Sudman, s.1982. Vragen stellen: een praktische gids voor vragenlijstontwerp. San Francisco. Jossey -bas.
- Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.
- Wonnacott, T.H. en r.J. Wonnacott. 1990000000000000000. Inleidende statistieken. 5e ed. Wiley
- Wikipedia. Monsterfout. Opgehaald uit: in.Wikipedia.com
- Wikipedia. Foutmarge. Opgehaald uit: in.Wikipedia.com
- « Inferentiële statistiekengeschiedenis, kenmerken, waarvoor is het voor voorbeelden
- U -Test van Mann - Whitney Wat is en wanneer van toepassing, uitvoering, voorbeeld »

