Formule en vergelijkingen spanningsinspanning, berekening, oefeningen

Hij Stressspanning Het wordt gedefinieerd als de kracht loodrecht op het gebied per gebied van eenheid die wordt uitgeoefend op een object aan de uiteinden om er tractie op te oefenen, waarmee het verlengt. De dimensies zijn van kracht / gebied en in wiskundige vorm kunnen we het als volgt uitdrukken:

τ = f / a

De eenheid van de inspanning in het internationale systeem van eenheden is hetzelfde dat wordt gebruikt voor druk: de Pascal, afgekort PA, die gelijkwaardig is aan 1 Newton/ m².

Figuur 1. Als de spanningsinspanning een bepaalde waarde overschrijdt, is het touw verbroken. Bron: Pxhere.

In de spanningsinspanning zijn er twee krachten die in dezelfde richting en tegenovergestelde zintuigen van toepassing zijn, die het lichaam strekken. Als oorspronkelijk de lengte van het object l was_of, Bij het toepassen van de spanningsinspanning is de nieuwe lengte L en wordt het AL -stretchen berekend door:

Δl = l - l_of

Solide objecten hebben in meer of mindere mate elasticiteit, wat betekent dat wanneer de spanningsinspanning verdwijnt, ze terugkeren naar hun oorspronkelijke dimensies.

Dit gebeurt op voorwaarde dat de inspanning niet zo groot is om permanente vervorming te veroorzaken. Rubber-, rubber- of rubberen materialen zijn goed voor elastische objecten en hebben ook deze kwaliteit haar en huid, onder andere.

[TOC]

Unitaire vervorming

Bij het bestuderen van hoe lichamen vervormen onder spanning, is het erg handig om het concept van te definiëren Unitaire vervorming, Een losgelaten hoeveelheid. Unitaire vervorming wordt aangegeven door de Griekse letter 8 (kleine letters "delta") en wordt als volgt berekend:

Δ = Δl /l_of

Unitaire vervorming dient om de vervorming van het object onder spanning relatief te beoordelen. Laten we het op deze manier zien: het is niet hetzelfde om 1 cm een ​​balk van 1 meter lang te strekken, om 1 cm tot nog eens 10 m lang te strekken. In het eerste geval is vervorming veel belangrijker dan in de tweede.

Het kan u van dienst zijn: OHM: weerstandsmaatregelen, voorbeelden en oefening opgelost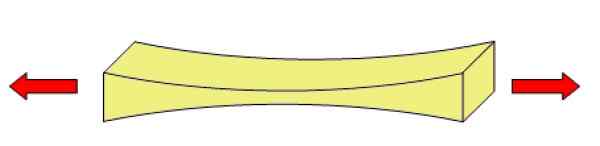Figuur 2. Een object dat een spanning of tractie -inspanning ondergaat, is vervormd. Bron: Wikimedia Commons.

Hoe wordt de spanningsinspanning berekend?? (Voorbeelden)

Newton's Engelse en hedendaagse natuurkundige genaamd Robert Hooke (1635-1703), onderzocht de elastische eigenschappen van de lichamen en vestigde de wet die zijn naam draagt. Hiermee is de inspanning die wordt toegepast op de vervorming die wordt ervaren wanneer de inspanning klein is, gerelateerd:

Inspanning ∝ vervorming (unital)

Het is logisch om te verwachten dat hoe groter de stressinspanning, een grotere verlenging zal optreden. Gebruik maken van de hierboven gegeven definities:

τ ∝ δ

De evenredigheid die nodig is om gelijkheid vast te stellen wordt aangeduid en staat bekend als de jonge module of elasticiteitsmodule, kenmerkend voor de materialen:

τ = y⋅δ

De module van Young heeft dezelfde eenheden van spanningsinspanning, omdat de vervorming van de eenheid dimensieloos is.

Dus een manier om de stressinspanning in een lichaam met elastische eigenschappen te berekenen, is het meten van vervorming en het kennen van de jonge module. Deze hoeveelheid is voor veel materialen experimenteel bepaald en is getabeld.

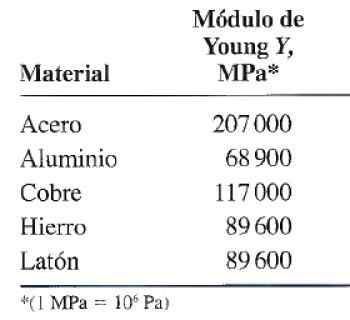figuur 3. Young's elasticiteit of modulemoduletabel voor wat gemeenschappelijk gebruiksmateriaal. Bron: Valera Negrete, J. 2005. ALGEMENE FYSICA -NOTIES. UNAM.

Voorbeeld van berekening

Stel dat een gehard staal met een diameter van 3 mm wordt onderworpen aan een spanningsinspanning, waardoor er een gewicht van 250 N aan hangt, wat de omvang van de genoemde inspanning zou zijn?

Welnu, we kunnen de definitie van spanningsinspanning gebruiken als het quotiënt tussen de kracht loodrecht op het oppervlak en het gebied van genoemde oppervlak. Laten we eerst het gebied berekenen, uitgaande van een cirkelvormige dwarsdraad:

Het kan u van dienst zijn: Massalummer: wat is het en hoe u het kunt krijgen (met voorbeelden)

A = π . (D/2)² =  π . (D² /4)

De diameter van de draad is 3 mm en deze eenheden moeten worden omgezet in meters:

D = 3 x 10^-3 M.

A = π . (3 x 10^-3 M)² / 4 = 7.07 x 10^-6 M².

De spanningsinspanning wordt geproduceerd door het gewicht dat aan de draad hangt, dat loodrecht op de dwarsdoorsnede wordt toegepast, daarom:

τ = 250 n / 7.07 x 10^-6 M² = 3.5 x 10 ⁷ vader

De Pascal is een vrij kleine eenheid, dus de veelvouden zijn niet ongebruikelijk. Weten dat 1 mega-pascal (MPA) 10 is⁶ Pascal, de spanningsinspanning blijft:

τ = 35 MPa

Opgeloste oefeningen

- Oefening 1

De elasticiteitsmodule van een staaf is 4 x 10^elf vader. Welke eenheidsvervorming wordt verkregen door een spanningsinspanning van 420 MPa toe te passen?

Oplossing

De te gebruiken vergelijking is:

τ = y⋅δ

Hiermee berekenen we de unitaire vervorming:

Δ = τ / y = 420 x 10⁶ PA/ 4 x 10^elf PA = 0.00105

Δ = Δl /l_of

Daarom is de vervorming AL:

Δl = 0.00105 L_of

Als de staaf bijvoorbeeld oorspronkelijk 1 meter lang was, met die spanningsinspanning strekt hij zich uit slechts 0.00105 m = 1.05 mm.

- Oefening 2

Een staaldraad heeft 1.50 m lang en een diameter van 0.400 mm. Een van de uiteinden is aan het dak bevestigd en een massameflector wordt op de andere geplaatst M = 1.50 kg, die wordt vrijgegeven. Berekenen:

A) Draadrek.

b) Unitaire vervorming en eenheidspercentage. Is het mogelijk dat de draad wordt verbroken door het gewicht van de reflector?

Oplossing

De draad gaat uitrekken, omdat de reflector wordt onderworpen aan een spanningsinspanning. De kracht die door deze inspanning wordt geproduceerd, is het gewicht van de reflector.

Het kan je van dienst zijn: natuurkunde voor de Grieken (Antigua Griekenland)

Het gewicht van een massaobject is het product van de massa door de waarde van de versnelling van de zwaartekracht, daarom:

F = 1.50 kg x 9.8 m/s² = 14.7 n

De kruising van het draadgedeelte is nodig:

A =  π . (D² /4) = π x (0.4 x 10-3 m) 2/4 = 1.26 x 10^-7 M².

Met deze resultaten wordt de inspanning op de draad berekend:

τ = 14.7 N / 1.26 x 10^-7 M² = 1.17 x 10⁸ vader

De draad heeft een elastisch gedrag, daarom is het geldig om aan te nemen dat de wet van Hooke is vervuld:

τ = y⋅δ

Uit de elasticiteitsmoduletabel vinden we dat voor staal y = 207 x 10⁹ vader. Bovendien is unitaire vervorming:

Δ = Δl /l_of

Vervangen in de vergelijking voor de inspanning:

τ = y⋅δ = y⋅ (Δl /l_of))

Daarom is het strekken:

Δl = l_of τ / y =

= 1.50 m x 1.17 x 10⁸ PA / 207 x 10⁹ PA = 8.5 x 10^-4 M = 0.849 mm.

De unitaire vervorming van de draad is:

Δ = Δl /l_of = 8.5 x 10^-4 m / 1.5 m = 5.652 x 10^-4

Als we het als een percentage uitdrukken, is het percentage unitaire vervorming 0.0565 %, minder dan 0.1 %, daarom wordt verwacht dat de draad het reflectorgewicht weerstaat zonder te breken, omdat de vervorming die het ervaart niet te groot is in vergelijking met de oorspronkelijke lengte.

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Bier, f. 2010. Materiaalmechanica. McGraw Hill. 5e. Editie.
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1.
5. Valera Negrete, J. 2005. ALGEMENE FYSICA -NOTIES. UNAM.