Rotatie -balansformules en -vergelijkingen, voorbeelden, oefeningen

Er wordt beweerd dat er een uitgebreide lichaam in is rotatiebalans Wanneer de som van de knooppunten die erop werken nul is. Dit betekent niet dat het object noodzakelijkerwijs in rust is, maar eerder dat er geen netto trend is om de staat van beweging te veranderen in een ander.

Een object dat met constante snelheid beweegt, doet dit langs een rechte lijn en we kunnen het in rotatiebalans beschouwen. Nu draaien objecten omdat er krachten zijn die op hen op een zodanige manier handelen dat het een rotatie is. Het vermogen van een kracht om rotatie te produceren, koppel genoemd of Torca, Het hangt niet alleen af ​​van de intensiteit van de kracht, maar ook waar het wordt toegepast.

Figuur 1. De hangbrug van de figuur was ontworpen om in balans te zijn. Bron: Wikimedia Commons.

We herkennen dit onmiddellijk wanneer een gesloten deur gaat openen: de kracht wordt nooit in de buurt van de scharnieren aangebracht, maar ver van hen, dus het handvat wordt zo ver mogelijk geplaatst, naast de deur van de deur.

De scharnieren passeren de rotatieas van de deur. Je erop aandringen het heel dicht bij de scharnieren te duwen, je moet een grote inspanning doen voor de deur om zelfs een beetje te bewegen.

In de literatuur staat het koppel met verschillende namen: moment van torsie, torsie, moment van een kracht en torca. Het zijn allemaal synoniemen.

We moeten dus de koppels kennen die op een object handelen om de rotatie -balansvoorwaarde vast te stellen.

[TOC]

Rotatiebalansconditie

De rotatiebalansconditie is:

De som van alle momenten of koppels die op een lichaam werken, berekend met betrekking tot elke as, moet nietig zijn.

Het object in kwestie moet worden uitgebreid, omdat deeltjes per definitie alleen een vertaalbalans hebben.

U kunt u van dienst zijn: de tweede wet van Newton: aanvragen, experimenten en oefeningen

Er kunnen krachten op het lichaam worden uitgeoefend en er is nog steeds een rotatiebalans, terwijl de krachten het niet draaien.

Er kan ook beweging zijn, zelfs versneld, maar altijd langs een rechte lijn, omdat niet alle krachten het uiterlijk van Turques veroorzaken. Deze verschijnen wanneer de krachten niet in dezelfde werklijn handelen.

Koppel of moment van kracht

Het koppel wordt aangeduid met de Griekse teksten τ, in dikgedrukt lettertype Omdat het een vector is en we het onderscheiden van zijn grootte of module, wat een scalair is. Het hangt af van de uitgeoefende kracht F, van de vector R die is gericht vanuit de rotatieas of op het punt van toepassing van de kracht en ten slotte, van de hoek tussen deze twee vectoren.

De juiste relatie tussen deze magnitudes wordt vastgesteld via het vectorproduct:

τ = r X F

En de koppelmodule, zonder vet aangeduid is:

τ = r⋅f⋅Sen θ

Waar θ de hoek is tussen R En F. Koppeleenheden zijn gewoon N⋅m in het internationale systeem.

In de figuur is er een Engelse sleutel waarmee deze is bedoeld. Hiervoor worden twee krachten geprobeerd F_NAAR En F_B.

F_NAAR is dichter bij O en heeft een vector R_NAAR of kortere hendelarm, produceert daarom niet zoveel koppel en kracht F_B, Dat heeft dezelfde omvang, maar het heeft een vector R_B groter.

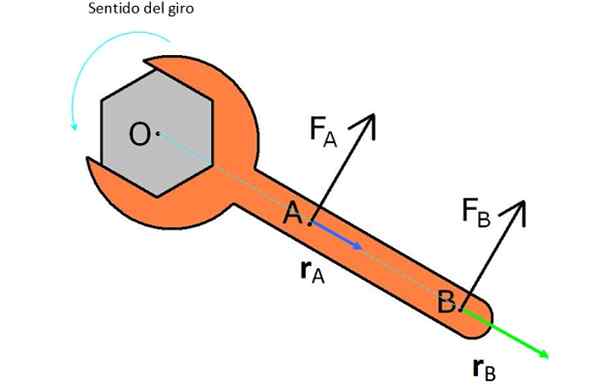Figuur 2. Krachten en armen toegepast op een Engelse sleutel om het in tegenstelling tot de kloknaalden te draaien. Bron: Wikimedia Commons.

Merk op dat als u de moer in een schema wilt roteren, u de krachten in de tegenovergestelde richting moet aanbrengen op hoe ze in de figuur verschijnen.

Richting en gevoel van koppel

Aangezien het koppel voortvloeit uit het kruisproduct tussen de sterkte- en positievectoren, en deze zijn in het vlak van de Engelse sleutel, moet het koppel een vector loodrecht op dat vlak zijn, dat wil zeggen gericht op de lezer of binnen de pagina.

Kan u van dienst zijn: atmosferische druk: normale waarde, hoe het wordt gemeten, voorbeelden

Volgens de conventie is het koppel positief als het beurt in de tegenovergestelde richting van de kloknaalden produceert, en negatief als dit in de richting van de klok doet.

De richting en richting van het resulterende koppel worden gemakkelijk bepaald door de regel van de onderstaande rechterhand:

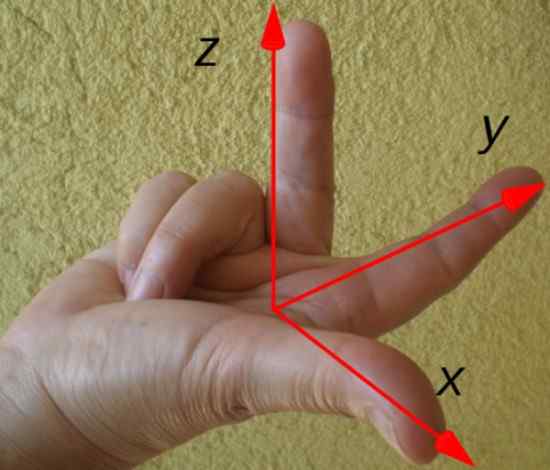figuur 3. Rechterhandregel om de richting en richting van de troca te bepalen. Bron: Wikimedia Commons.

De wijsvinger wijst volgens de positievector R, De middelvinger volgens geweld F En de duim geeft de richting en richting van het koppel aan τ. In dit voorbeeld wordt het koppel gericht langs de X -as, volgens de tekening van de coördinaatassen.

Formules en vergelijkingen

Als de knooppunten op een lichaam handelen τ₁, τ_2, τ_3… τ_Je, Het net of het resulterende koppel τ_N Het is de vector som van ze allemaal:

τ_N = τ₁+ τ₂ +  τ₃ +_.. τ_Je

Met een samenvatting van de samenvatting blijft het:

τ_N = ∑ τ_Je

De evenwichtstoestand wordt als volgt wiskundig uitgedrukt:

τ_N = 0

O goed:

∑ τ_Je = 0

Waar het koppel τ, Wat betreft een bepaalde O -as, wordt deze berekend door:

τ = r X F

En wiens omvang is:

τ = r⋅f⋅Sen θ

Voorbeelden

-Bij mensen en dieren is gewicht een kracht die koppel kan veroorzaken en draaien en vallen.

Mensen handhaven meestal een dergelijke positie dat ze bij het lopen in balans houden van rotatie, tenzij sportactiviteit wordt beoefend, zoals gymnastiek, schaatsen of sporten in het algemeen.

-Twee kinderen die erin slaagden om horizontaal te blijven in de rocker of omhoog en omlaag Ze zijn in rotatiebalans.

-Wanneer de schotels van de balans in evenwicht zijn, bevindt het systeem zich in rotatie -evenwicht.

-Kennisgevingen en verkeerslichten die aan straten en wegen hangen, zijn ook in rotatiebalans. Als de kabels die ze vasthouden zijn verbroken, gaat dit evenwicht verloren en hangt de kennisgeving of valt.

Het kan u van dienst zijn: gemiddelde versnelling: hoe het wordt berekend en opgelost

-Hangende bruggen zoals Golden Gate in San Francisco en de brug van figuur 1.

Oefening opgelost

De balk ondersteund door een ondersteuning in de figuur is erg licht. De kracht die door ondersteuning wordt uitgeoefend, is F en aan het einde is de kracht van toepassing NAAR.

Er wordt gevraagd om de grootte van deze krachten te berekenen, aangezien het systeem in evenwicht is van vertaling en rotatie.

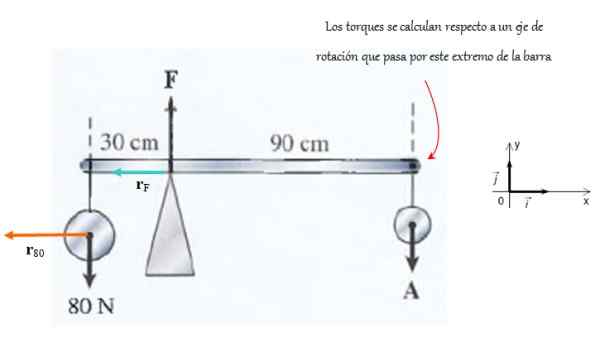Figuur 4. Op deze bar werken krachten op een zodanige manier dat het in rotatie -evenwicht blijft. Bron: f. Zapata.

Oplossing

Aangezien het systeem niet beweegt, wordt de som van krachten geannuleerd. Ze zijn allemaal verticaal en je kunt werken met de magnitudes. De positieve zin is daarom en het negatieve down:

F - 80 - A = 0

Nu wordt de rotatie -evenwichtstoestand toegepast, waarvoor u een willekeurige rotatieas moet kiezen. In dit geval wordt het aan het einde gekozen, zodat de vector R_NAAR Wees nietig, op deze manier het koppel uitgeoefend door NAAR, maar alleen die van F en de kracht van de linker.

Het koppel geproduceerd door F Het is volgens de regel van de rechterhand en het getoonde coördinatensysteem:

τ_F = R_F X F = 0.9 F (-k) N.M

Het is gericht in het scherm en heeft een negatief teken. Terwijl het koppel geproduceerd door de kracht van 80 N is:

τ = 80 x 1.twintig (k) N⋅m = 96 (k) N⋅m

Dit koppel is uit het scherm gericht en krijgt een positief teken toegewezen. Omdat er rotatiebalans is:

96 - 0.9⋅f = 0

De omvang van F is:

F = (96/0.9) n = 106.7 n

En omdat het systeem zich in de vertaalbalans bevindt, wordt de som van de krachten geannuleerd. Hierdoor kunnen we de omvang van NAAR:

F - a - 80 n = 0

Daarom:

A = 106.7 - 80 n = 26.7 n.

Referenties

1. Rex, a. 2011. Fundamentals of Physics. Pearson.
2. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.
3. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. Pearson.
4. Tipler, p. (2006) Natuurkunde voor wetenschap en technologie. 5e ed. Deel 1. Redactioneel teruggekeerd.
5. Tippens, p. 2011. Fysica: concepten en toepassingen. 7e editie. McGraw Hill.