Mechanische energieformules, concept, typen, voorbeelden, oefeningen

De mechanische energie van een object of systeem wordt gedefinieerd als de som van zijn potentiële energie en zijn kinetische energie. Zoals de naam al aangeeft, verwerft het systeem mechanische energie dankzij de werking van mechanische krachten zoals gewicht en elastische kracht.

Volgens de hoeveelheid mechanische energie die het lichaam heeft, zal het ook de mogelijkheid hebben om een ​​mechanisch werk uit te voeren.

Figuur 1. De Roller Mountain Car Movement kan worden beschreven door het behoud van mechanische energie. Bron: Pixabay.

De energie - het type dat is - is een scalaire hoeveelheid, daarom ontbrekende richting en betekenis. Zijn EN_M De mechanische energie van een object, OF zijn potentiële energie en K Zijn kinetische energie, de formule om te berekenen is:

EN_M = K + u

De eenheid in het internationale energiesysteem van welke aard dan ook is de joule, die wordt afgekort als J. 1 J is gelijk aan 1 n.M (Newton per meter)).

Wat betreft kinetische energie, het wordt als volgt berekend:

K = ½ m.v²

Waar M Het is de massa van het object en v Zijn snelheid. Kinetische energie is altijd een positieve hoeveelheid, omdat de massa en het kwadraat van de snelheid zijn. Wat betreft potentiële energie, als het gaat om zwaartekracht potentieel energie, heb je:

U = m.G.H

Hier M Het is nog steeds het deeg, G Het is de versnelling van de zwaartekracht en H Het is de hoogte ten opzichte van het referentieniveau of indien gewenst, de grond.

Nu, als het lichaam in kwestie elastische potentiële energie heeft -het kan een veer zijn -het komt omdat het wordt gecomprimeerd of misschien langwerpig. In dat geval is de bijbehorende potentiële energie:

U = ½ kx²

Met k als de veerconstante, wat aangeeft hoe gemakkelijk of moeilijk het is om het te vervormen en X De lengte van genoemde vervorming.

[TOC]

Concept en kenmerken van mechanische energie

Door de eerder gegeven definitie te verdiepen, hangt mechanische energie dan af van de energie geassocieerd met lichaamsbeweging: kinetische energie, plus de bijdrage van potentiële energie, die zoals we al zei zwaartekracht kan zijn, zowel vanwege gewicht als aan gewicht en positie die het lichaam bezet met respect voor de bodem of referentieniveau.

Laten we dit illustreren met een eenvoudig voorbeeld: stel dat u een pot op de vloer en in rust hebt. Omdat het nog steeds is, heeft het geen kinetische energie, en het is ook op de grond, een plaats van waar het niet kan vallen; Daarom mist het zwaartekracht potentieel energie en de mechanische energie is 0.

Stel nu dat iemand de pot net aan de rand van een dak of een raam plaatst, op 3.0 meter hoog. Hiervoor moest de persoon een baan doen tegen de zwaartekracht. De pot heeft nu zwaartekracht potentieel energie, het kan van die hoogte vallen en de mechanische energie is niet langer ongeldig.

Figuur 2. Een pot bovenop een raam heeft zwaartekracht potentieel energie. Bron: Pixabay.

In deze omstandigheden heeft de pot EN_M = U En deze hoeveelheid hangt af van de lengte en het gewicht van de pot, zoals eerder aangegeven.

Laten we zeggen dat de pot valt omdat deze in een precaire positie was. Naarmate de snelheid toeneemt en daarmee zijn kinetische energie, terwijl de zwaartekrachtpotentiaal energie afneemt, omdat het hoogte verliest. De mechanische energie op elk moment van de herfst is:

Kan u van dienst zijn: wat zijn de afgeleide magnitudes?

EN_M = U + k = ½ m.v² + M.G.H  

Conservatieve en niet-conservatieve krachten

Wanneer de pot op een bepaalde hoogte is, heeft het zwaartekracht potentieel energie omdat wie er klimt, een werk tegen de zwaartekracht aan. De omvang van dit werk is hetzelfde waard als degene die de zwaartekracht maakt wanneer de pot valt af Van dezelfde hoogte, maar het heeft het tegenovergestelde teken, omdat het ertegen is gemaakt.

Het werk dat krachten zoals zwaartekracht en elasticiteit alleen hangt af van de initiële positie en de eindpositie verkregen door het object. Ongeacht het traject dat volgde om van de ene naar de andere te gaan, alleen de waarden zelf doen er toe. De krachten die zich op deze manier gedragen, worden genoemd Conservatieve krachten.

En omdat ze conservatief zijn, laten ze het werk dat door hen wordt verricht, als potentiële energie worden opgeslagen in de configuratie van het object of het systeem. Dat is de reden waarom de pot aan de rand van het raam of het dak de mogelijkheid had om te vallen, en daarmee om beweging te ontwikkelen.

Aan de andere kant zijn er krachten waarvan de werken afhankelijk zijn van het pad gevolgd door het object waarop ze handelen. De wrijving hoort bij dit soort krachten. Schoenenzolen worden meer besteed als je van de ene plaats naar de andere op een weg gaat met veel ronden, dan wanneer je voor een andere gaat.

Wrijvingskrachten doen een werk die de kinetische energie van de lichamen vermindert, omdat het hen vertraagt. En dat is de reden waarom de mechanische energie van de systemen waarin de wrijving werkt, de neiging heeft om af te nemen.

Een deel van het werk dat met geweld wordt gedaan, gaat bijvoorbeeld verloren door warmte of geluid.

Soorten mechanische energie

Mechanische energie is, zoals we zeiden, de som van kinetische energie en potentiële energie. Nu kan potentiële energie voortkomen uit verschillende conservatieve krachten: gewicht, elastische sterkte en elektrostatische kracht.

- Kinetische energie

Kinetische energie is een scalaire hoeveelheid die altijd de beweging wordt. Elk deeltje of bewegend object heeft kinetische energie. Een object dat in een rechte lijn beweegt, heeft kinetische vertalingsenergie. Hetzelfde gebeurt als het roteert, in dit geval is er sprake van rotatiekinetische energie.

Een auto die langs een weg beweegt, heeft bijvoorbeeld kinetische energie. Ook een voetbalbal terwijl je langs het veld gaat of de persoon die haastig loopt om het kantoor te bereiken.

- Potentiële energie

Het is altijd mogelijk om een ​​scalaire functie te associëren die potentiële energie wordt genoemd met een conservatieve kracht. De volgende worden onderscheiden:

Gravitationele potentieel energie

Degene die alle objecten hebben op grond van hun hoogte ten opzichte van de grond, of het referentieniveau dat als zodanig is geselecteerd. Als voorbeeld heeft iemand die in rust is op het terras van een gebouw met 10 storingen, potentiële energie 0 met betrekking tot de grond van het terras, maar niet met betrekking tot de straat die 10 verdiepingen lager is.

Elastische potentiële energie

Het wordt meestal opgeslagen in objecten zoals competities en veren, geassocieerd met de vervorming die ze ervaren bij het uitrekken of comprimeren van ze.

Elektrostatische potentiële energie

Het wordt opgeslagen in een systeem van elektriciteitsbelastingen in evenwicht, vanwege de elektrostatische interactie daartussen. Stel dat er op kleine afstand twee elektrische ladingen van hetzelfde afzonderlijke bord zijn; Omdat elektrische kosten van hetzelfde teken worden afgestoten, wordt verwacht dat een externe agent werk heeft gedaan om ze dichterbij te brengen.

Kan u van dienst zijn: Wisselingsstroomcircuits: typen, toepassingen, voorbeelden

Zodra het is geplaatst, slaagt het systeem erin het werk op te slaan dat de agent heeft gedaan om ze te configureren, in de vorm van elektrostatische potentiële energie.

Behoud van mechanische energie

Terugkerend naar de vallende pot, wordt de zwaartekrachtpotentiaal energie die het had toen het op de rand van het dak was omgezet in kinetische beweging van beweging. Dit neemt toe ten koste van de eerste, maar de som van beide blijft constant, omdat de val van de pot wordt geactiveerd door de zwaartekracht, wat een conservatieve kracht is.

Er is een uitwisseling tussen het ene type energie en het andere, maar de oorspronkelijke hoeveelheid is hetzelfde. Daarom is het geldig om te bevestigen dat:

Eerste mechanische energie = uiteindelijke mechanische energie

EN_{Eerste m} = E_{M finale}

Alternatief:

K_voorletter + OF_voorletter = K _laatste + OF_laatste

Met andere woorden, mechanische energie verandert niet en ∆E_M = 0. Het "∆" -symbool betekent variatie of verschil tussen een definitieve hoeveelheid en een initiaal.

Om het principe van behoud van mechanische energie correct toe te passen op probleemoplossing is het noodzakelijk om:

-Het is alleen van toepassing wanneer de krachten die op het systeem werken conservatief zijn (ernst, elastisch en elektrostatisch). In dat geval: ∆E_M = 0.

-Het studiesysteem moet worden geïsoleerd. Er is op geen enkele manier geen energieoverdracht.

-Als in een probleem frivatie verschijnt, dan ∆E_M ≠ 0. Toch kan het probleem worden opgelost door het werk te vinden dat door conservatieve krachten wordt gedaan, omdat het de oorzaak is van de afname van mechanische energie.

Aftrek van mechanische energiebesparing

Stel dat een conservatieve kracht werkt op het systeem dat een werk doet W. Dit werk veroorzaakt een verandering in kinetische energie:

W = ∆k (Cinetic Work-Energy Stelling)

Het is belangrijk op te merken dat de werk-energie-stelling Kinetic van toepassing is, zelfs in het geval van niet-conservatieve krachten.

Aan de andere kant is het werk ook verantwoordelijk voor de verandering in potentiële energie, en in het geval van een conservatieve kracht wordt de verandering in potentiële energie gedefinieerd als het negatieve van dat werk:

W = -∆U

Bij het matchen van deze vergelijkingen, omdat beide verwijzen naar het werk dat aan het object is gedaan:

∆k = -∆U 

K_F - K_of = -(u_F - OF_of))

Subscripts symboliseren "finale" en "initiaal". Groepering:

K_F + OF_F = K_of + OF_of                                                    

Voorbeelden van mechanische energie

Veel objecten hebben complexe bewegingen, waarin het ingewikkeld is om uitdrukkingen te vinden voor de positie, snelheid en versnelling als functie van de tijd. In dergelijke gevallen is het toepassen van het principe van mechanische energiebesparing een effectievere procedure dan proberen de wetten van Newton rechtstreeks toe te passen.

Laten we eens kijken naar enkele voorbeelden waarin mechanische energie wordt bewaard:

-Een skiër die bergafwaarts over besneeuwde heuvels glijdt, op voorwaarde dat afwezigheid van wrijving wordt verondersteld. In dit geval is het gewicht de oorzakelijke kracht van de beweging in het traject.

-Russische bergkarren, Het is een van de meest typische voorbeelden. Hier is ook het gewicht de kracht die beweging definieert en mechanische energie wordt bewaard als er geen wrijving is.

Kan u van dienst zijn: ionisatie -energie

-De eenvoudige slinger Het bestaat uit een massa die onderworpen is aan een niet -uitgelegd touw -het verandert niet de lengte -die kort scheidt van de verticaal en mag oscilleren. We weten dat het uiteindelijk zal stoppen vanwege wrijving, maar wanneer de wrijving niet wordt overwogen, wordt mechanische energie ook bewaard.

-Een blok dat een lente beïnvloedt Opgelost aan het ene uiteinde aan de muur, zetten ze allemaal een zeer gladde tafel op. Het blok comprimeert de veer, reist op een bepaalde afstand en wordt vervolgens in de tegenovergestelde richting afgevuurd, omdat de veer strekt. Hier verwerft het blok zijn potentiële energie dankzij het werk dat de lente erop maakt.

-Lente en bal: Wanneer een veer wordt gecomprimeerd door een bal, dit stuiteren. Dit komt omdat wanneer de veer wordt vrijgegeven, potentiële energie kinetische energie in de bal wordt.

-Trampolinesprong: Het werkt vergelijkbaar met een lente, het elastisch promoten van de persoon die op hem springt. Dit maakt gebruik van zijn gewicht tijdens het springen, waarmee het de trampoline vervormt, maar deze, bij terugkeer naar zijn oorspronkelijke positie, geeft de impuls aan de jumper.

figuur 3. De springplank fungeert als een veer en promoot de mensen die erop springen. Bron: Pixabay.

Opgeloste oefeningen

- Oefening 1

Een object van massa M = 1 kg wordt gedropt door een helling van een hoogte van 1 m. Als de helling extreem soepel is, berekent u de lichaamssnelheid net wanneer de veer botst.

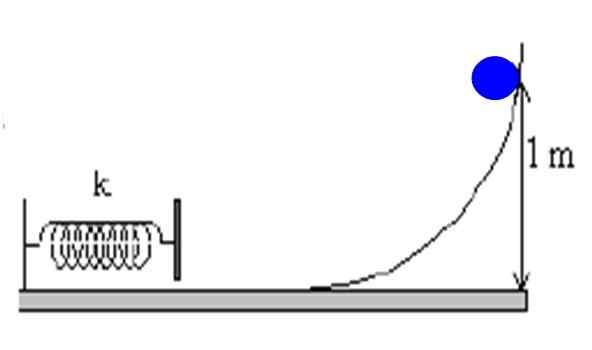Figuur 4. Een object daalt op een helling af zonder wrijving en somprimeert een veer die aan de muur is bevestigd. Bron: f. Zapata.

Oplossing

De verklaring meldt dat de helling soepel is, wat betekent dat de enige kracht die op het lichaam werkt zijn gewicht is, een conservatieve kracht. Daarom wordt aangegeven om het behoud van mechanische energie tussen alle punten van het traject toe te passen.

Overweeg de punten gemarkeerd in figuur 5: a, b en c.

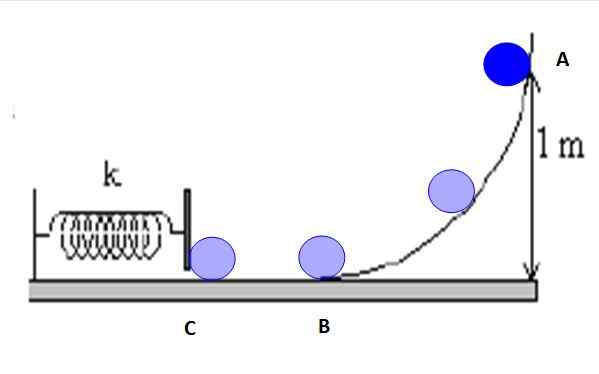Figuur 5. Het pad dat het object volgt, is wrijving en mechanische energie wordt bewaard tussen elk paar punten. Bron: f. Zapata.

Het is mogelijk om het behoud van energie tussen A en B, B en C of A en C of een van de tussenliggende punten op de helling vast te stellen. Bijvoorbeeld, tussen A en C heb je:

Mechanische energie bij A = mechanische energie in C

EN_ma = E_MC

K_NAAR + OF_NAAR = K_C + OF_C

½ m.v_NAAR² + M.G.H_NAAR = ½ m V_C² + M.G.H_C

Zoals wordt vrijgegeven uit punt A, de snelheid V_NAAR = 0, aan de andere kant h_C = 0. Bovendien wordt de massa geannuleerd, omdat deze een gemeenschappelijke factor is. Dus:

G.H_NAAR = ½ V_C²

v_C²= 2 g.H_NAAR

- Oefening 2

Zoek de maximale compressie die de veer van de oefening heeft opgelost, ik zal ervaren, als de elastische constante van hetzelfde 200 n/m is.

Oplossing

De elastische constante van de veer geeft aan dat de kracht moet worden toegepast om een ​​lengte -eenheid te vervormen. Aangezien de constante van dit voorjaar k = 200 N/m waard is, geeft dit aan dat 200 N vereist is om het te comprimeren of te rekken 1 m.

Zijn X De afstand die het object de veer comprimeert voordat hij stopt op punt D:

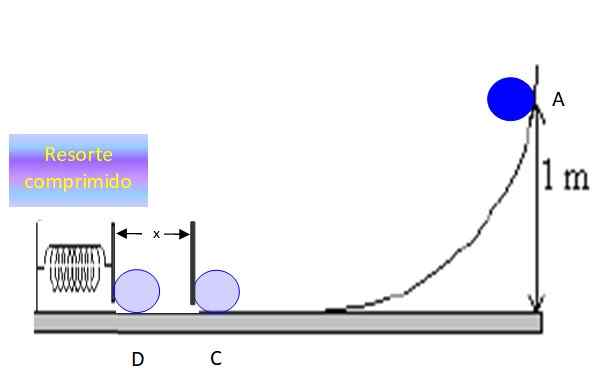Figuur 6. Het object comprimeert de veer een X -afstand en stopt even. Bron: f. Zapata.

Het behoud van energie tussen punten C en D stelt dat vast:

K_C + OF_C = K_D + OF_D

Op punt C heeft het geen zwaartekracht potentieel energie, omdat de hoogte 0 is, maar het heeft kinetische energie. In D is hij volledig gestopt, daarom k_D = 0, maar in plaats daarvan heb je ter beschikking de potentiële energie van de gecomprimeerde veer U_D.

Het behoud van mechanische energie blijft bestaan:

K_C = U_D

½ mV_C² = ½ kx²

 

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB).
3. Ridder, r.  2017. Fysica voor wetenschappers en engineering: een strategiebenadering. Pearson.
4. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1.
5. Wikipedia. Mechanische energie.Hersteld van: is.Wikipedia.borg.