Hendecagon

Wat is een endecagon?

Hij Hendecagon, ook wel genoemd Undecágono, Het is een platte geometrische figuur met 11 zijden die tot de Polygons -familie behoort.

Deze worden benoemd volgens de hoeveelheid kanten die ze hebben en in het geval van de endecagon is hun naam afgeleid van de Griekse woorden "Hendeka" en "Gona": respectievelijk elf en hoekpunt, volgens het feit dat de endecagon het heeft 11 hoekpunten of tips.

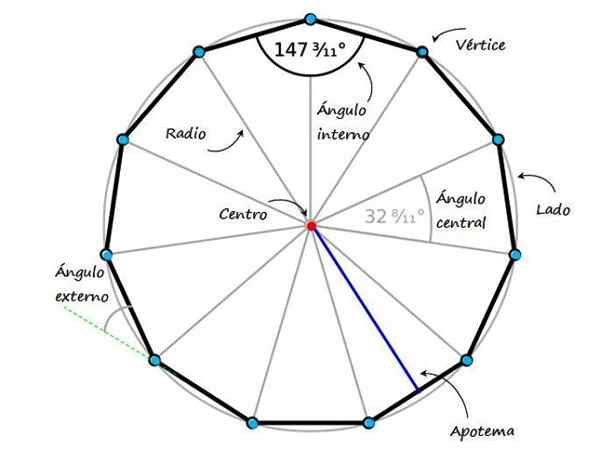
Figuur 1. Een regelmatige endecagon en zijn elementen. Bron: f. Gemodificeerde Wikimedia Commons -schoen.

Reguliere polygonen delen een reeks onderscheidende kenmerken, met name. Figuur 1 toont een gewone endecagon en de belangrijkste eigenschappen:

• Zijkanten, Een totaal van 11.
• Hoekpunten, Er zijn ook 11 punten die samenvoegen met twee opeenvolgende zijden (in de vorige figuur zijn de blauwe punten en in figuur 3 worden ze ook genoemd met hoofdletters).
• Centrum, Equidistant punt van zowel de hoekpunten als de zijkanten.
• Diagonalen, Lijnen die zich aansluiten bij een hoekpunt met een ander niet -opeenvolgend hoekpunt, in totaal 44.
• Interne hoeken, Degenen die worden gevormd tussen twee aangrenzende zijden aan de interne kant van de endecagon. Als de endecagon regelmatig is, meet alle interne hoeken 147 ^3/11 º.
• Externe hoeken, Ze worden gevormd tussen één kant en de verlenging van een van de opeenvolgende kanten.
• Radio, Afstand van het midden tot een hoekpunt.
• Centrale hoek, dat in het geval van reguliere endecagon meet 32 ^11/11 º, waarvan de zijkanten twee aangrenzende segmenten zijn en het hoekpunt van de hoek valt samen met het midden.
• Apothem, Ledigulair segment dat samen met het midden van de figuur het midden van één zijde verbindt.

Het kan je bedienen: Hipparco van Nicea: biografie en bijdragen aan de wetenschap

Hoe je een gewone endecagon maakt?

Om een ​​gewone endecagon te tekenen, wiens partijen hetzelfde meten, heb je regel en kompas nodig. Een manier om de lay -out te maken, is deze stappen volgen:

1.- Teken een omtrek en twee diameters ervan, een verticaal en een andere horizontaal. De punten van de omtrek bepaald door deze diameters worden genoemd en B (horizontale diameter) en C en D (verticale diameter).

2.- Open het kompas met de maat van de cirkelradius, ondersteun de punt op punt D van de CD -diameter en teken een eerste boog die de omtrek op punt E kruist.

3.- Met dezelfde maatregel ondersteunen de punt van het kompas op punt A en teken een tweede boog die de omtrek op punt F kruist en tegelijkertijd door het midden van hetzelfde gaat.

4.- Open de beat met de tip ondersteund door E en om F te punt,, tekenen een derde boog die de verticale diameter snijdt op punt G.

5.- Open nu het kompas tussen punten F en G. Dit is de maat van de endecagon -zijde. De punt van het kompas wordt ondersteund in F en trekt een vierde boog die naar de omtrek op punt H snijdt, de FH -zijde behoort al tot de endecagon en wordt getekend door de punten aan te sluiten met de hulp van de regel.

6.- De punt van het kompas rust achtereenvolgens op punt H en wordt zorgvuldig opgesteld en verbinden zich aan de punten die worden bepaald door segmenten, tot de elf zijden van de polygoon.

Voorbeelden van endecágonos

Er zijn verschillende soorten endecargons, volgens de maat van hun zijden en die van hun interne hoeken, onder enkele voorbeelden:

Regelmatige en onregelmatige endeconists

-Normaal, Als alle partijen en interne hoeken hetzelfde meten.

Kan u van dienst zijn: Euler -nummer of nummer E: hoeveel OK, eigenschappen, applicaties

-Onregelmatig, Wanneer hun partijen een andere maatregel hebben.

De volgende figuur toont een reguliere endecagon in de interne contour van een Amerikaanse dollar met de figuur van Susan B. Anthony (1820-1906), een activist van vrouwenrechten geboren in Massachusetts, Verenigde Staten. De endecagon is ook gebruikt als onderdeel van het ontwerp van andere munten over de hele wereld.

Figuur 2. Een regelmatige endecagon die deel uitmaakt van het Dollar Susan B -ontwerp. Anthony, bedacht tussen 1979 en 1981, en later opnieuw gelanceerd in 1999. Bron: Wikimedia Commons.

Convexe en concave endecargons

Endecargons verschillen volgens hun interne hoeken, bijvoorbeeld kunnen ze zijn:

-Convex, Als de interne hoeken minder zijn dan 180º.

-Concaaf, Als er interne hoeken zijn groter dan 180º.

De endecagon die de dollar susan b versiert. Anthony is convex, omdat de maat van een van zijn interne hoeken minder is dan 180º. De waarde ervan wordt berekend via een formule die afhankelijk is van het aantal zijden op de figuur (zie de volgende sectie).

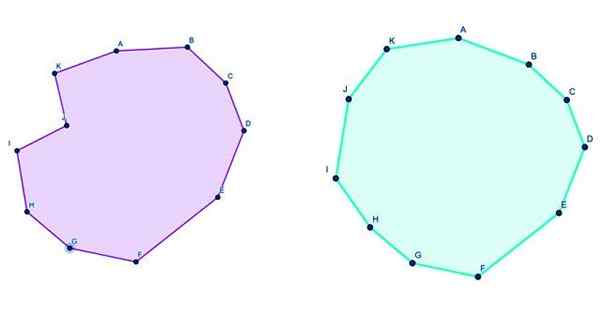figuur 3. Links een convexe endecagon en rechts een concave endecagon. Bron: f. Zapata door Geogebra.

Formules voor de endecagon

Formule voor interne hoeken

Om de maat I in graden te bepalen, van de interne hoeken van een reguliere polygoon van N zijkanten, de volgende formule wordt gebruikt:

 Het aantal zijden van de endecagon n = 11 in de formule wordt vervangen:

 En omdat de interne hoeken van de reguliere endecagon minder dan 180º zijn, is dit cijfer een convexe polygoon.

De som van de interne hoeken van een gewone polygoon wordt gevonden door deze formule, geldig voor geheel en groter dan 2:

Kan u van dienst zijn: hoeken in de omtrek: typen, eigenschappen, opgeloste oefeningen

S = (n - 2) x 180º

N = 11 resultaten vervangen:

S = (11 - 2) x 180º = 1620º

Externe hoeken

Om de maat voor interne hoeken te kennen, wordt toegepast dat de som van een interne en een externe hoek gelijk is aan 180º:

180 º - 147 ^3/11º = 32 ^11/11º.

Omtrek

De omtrek is de som van de zijkanten van de endecagon, nu regelmatig of niet. In het geval van reguliere endecagon, als ℓ Het is de lengte van één kant, de perimeter vermenigvuldigt zich met N, Het aantal zijden.

Daarom is de perimeter P van de reguliere endecagon:

P = 11 ℓ

Gebied

De zijkant kennen, kan het gebied worden berekend met de formule:

Dat is ongeveer:

A = 9.3656 ∙ ℓ²

Een andere manier om het gebied te vinden, op voorwaarde dat de endecagon regelmatig is, is door het te verdelen in basisdriehoeken gelijk aan de zijkant ℓ en hoogte gelijk aan de lengte van de apothem l l l l l l l l l_NAAR.

Het gebied van elke driehoek wordt berekend door:

Gebied = basis x hoogte /2

Dat afhankelijk van Apothem ook wordt geschreven als:

Gebied = ℓ. L_NAAR /2

En de totale oppervlakte van de endecagon vermenigvuldigt het driehoekgebied met 11:

A = 11ℓ. L_NAAR /2

In termen van de omtrek is het reguliere endecagon -gebied:

A = P. L_NAAR /2

Diagonalen

Het aantal diagonalen wordt berekend door n = 11 te doen in de volgende formule:

 D = [11 x (11-3)]/2 = 44 diagonalen.

Oefening opgelost

Bereken perimeter en oppervlakte van een gewone endecagon van 20 cm zijde.

Oplossing

De omtrek is:

P = 11 ℓ =11 × 20 cm = 220 cm.

En het gebied is:

A = 9.3656 ∙ ℓ²= 9.3656 × (20 cm)²= 3746.2 cm²

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Tekenaar professor. Endecágono ingeschreven in een omtrek (11 zijden polygoon). Hersteld van: YouTube.com.
3. Problemen en vergelijkingen. Gebied en perimetercalculator van de reguliere endecagon. Opgehaald uit: problemen Syuses.com.
4. Sangaku -wiskunde. Elementen van een polygoon en zijn classificatie. Hersteld van: Sangakoo.com.
5. Automatische geometrie probleemoplossing. De endecagon. Hersteld van: Scuolaetrica.Item.
6. Wolfram Mathworld. Hendecagon. Hersteld van: Mathworld.Wolfraam.com.