Absolute waarde

Wat is de absolute waarde?

Hij absolute waarde van een reëel getal wordt gedefinieerd als de afstand tussen dat aantal en 0 van de echte lijn. Om een ​​afstand te zijn, is de waarde ervan altijd positief of nul en gelijk aan de figuur van het getal.

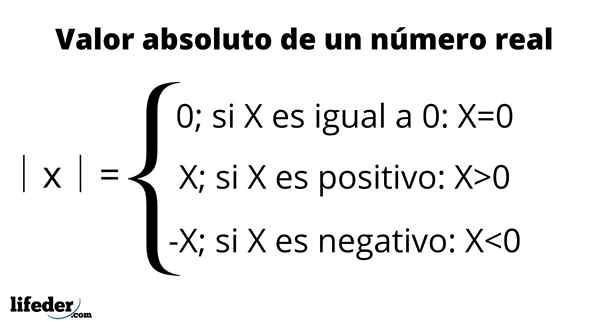
De absolute waarde wordt weergegeven door het nummer tussen twee verticale balken te plaatsen, een symbool dat wordt gelezen: "absolute waarde van”, Zoals samengevat in de volgende tabel:

De absolute waarde van -3 is bijvoorbeeld geschreven als │ -3│ en is gelijk aan 3. Dit betekent dat er tussen -3 en 0 drie eenheden zijn, die de cijfers op de echte lijn vertegenwoordigen. Aan de andere kant is de absolute waarde van +3 of eenvoudig 3 ook gelijk aan 3, omdat het door zijn afstand tot 0 te meten ook drie eenheden is.

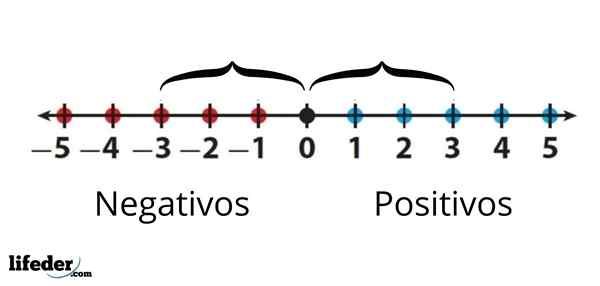De absolute waarde van -3 is gelijk aan de absolute waarde van +3, omdat de afstand tussen beide tot 0 hetzelfde is, is hetzelfde

Samenvattend is de absolute waarde van een getal hetzelfde cijfer van het getal, maar altijd met een positief teken.

Eigenschappen van absolute waarde

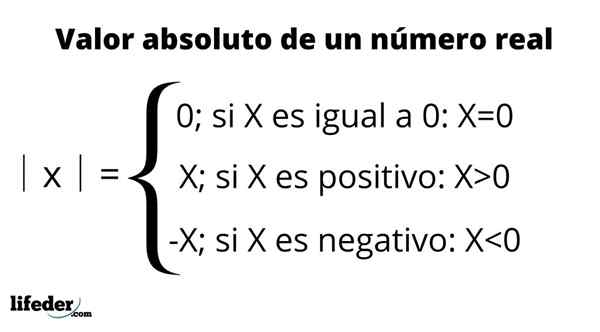Definitie van absolute waarde

De belangrijkste eigenschappen van absolute waarde:

• 1) De absolute waarde van een getal is daarom altijd positief of 0:

│x│ ≥ 0

• 2) De absolute waarde van nul is ook nul, dat wil zeggen │0│ = 0, daarom kan worden bevestigd dat:

│x│ = 0, ja y alleen als x = 0

• 3) Voor elk getal x dat tot de set reële getallen behoort, is de absolute waarde van X gelijk aan de absolute waarde van - x:

│x│ = │ - x│

• 4) Als de absolute waarde van een X -nummer A is, betekent dit dat er twee opties zijn voor dat nummer: i) x = +a of ii) x = -a.

Het kan je van dienst zijn: Mary reist 2/4 van de CyclePist, Melissa Travels 4/8 en Anahi reist 3/6

Als bijvoorbeeld de absolute waarde van een nummer 5 is, zijn de twee mogelijkheden dat het nummer +5 of -5 is.

Bewerkingen met absolute waarde

De volgende eigenschappen zijn zeer nuttig om bewerkingen met absolute waarden uit te voeren:

• 5) Voor "x" en "y" die twee reële getallen zijn, wordt de volgende ongelijkheid altijd vervuld, genaamd driehoekige ongelijkheid van absolute waarde:

│x│+│y│ │ │x+y│

Bijvoorbeeld:

x = -6

y = 9

De linkerkant van ongelijkheid is:

│-6│ + │9│ = 6 + 9 = 16

En de rechterkant is:

│-6+9│ = │3│ = 3

Het is duidelijk dat 16 groter is dan of gelijk is aan 3, en dit is altijd het geval wanneer de getallen x en verschillende tekenen hebben. Als ze gelijke tekenen hebben, wordt gelijkheid verkregen. Zie dit andere voorbeeld met twee andere verschillende waarden:

x = -5

y = -3

│-5│+│-3│ │ │-5-3│

5+3≥│-8│

Inderdaad:

8 = 8

• 6) Het product van de respectieve absolute waarden van twee reële getal "x" en "y" is gelijk aan de absolute waarde van het product van de getallen:

│x│ ∙ │y│ = │x ∙ y│

Opnieuw zijn de waarden:

x = -6

y = 9

Dus:

│-6│ ∙ │9│ = 6 ∙ 9 = 54

Die gelijk is aan:

│ (-6) ∙ 9│ = │-54│ = 54

• 7) Het quotiënt van de absolute waarde van twee reële getallen "X" en "Y", met de verschillende noemer van 0, is de absolute waarde van het quotiënt tussen deze getallen:

Zolang en ≠ 0.

Voorbeeld:

Voorbeelden van absolute waarde

Eenvoudige voorbeelden

Het berekenen van de absolute waarde van elk reëel getal is heel eenvoudig, bijvoorbeeld de absolute waarde van de volgende nummers is:

a) │-14│ = 14

b) │-(-5) │ = │5│ = 5

c) │π│ = π

Berekeningen met de absolute waarde van een reëel getal

Voer de volgende bewerkingen uit die de absolute waarde inhouden:

a) 2⋅│8│ + 5⋅│ -16│-⋅│4│ = (2⋅8) + (5⋅16) - 4 = 16 + 80 - 4 = 92

b) │5- (8⋅3) │- 6 + │81 ÷ (-3) │ 

Kan u van dienst zijn: de helft van 15

Dit is een gecombineerde bewerking, dus het heeft de voorkeur om het op te lossen met stappen. De eerste absolute waarde is:

│5- (8⋅3) │ = │5-24│ = │-19 │ = 19

De tweede absolute waarde die verschijnt, wordt als volgt berekend:

│81 ÷ (-3) │ = │-27│ = 27

Vervolgens worden de verkregen resultaten verzameld en wordt de uiteindelijke berekening uitgevoerd:

│5- (8⋅3) │- 6 + │81 ÷ (-3) │ = 19-6 + 27 = 40

De afstand tussen twee punten op de echte lijn

De absolute waarde verschijnt in veel toepassingen, zoals het vinden van de afstand tussen twee getallen die tot de echte lijn behoren. Als A een reëel getal is, bevindt het zich op de echte lijn op het punt waarvan de abscis "A" is, gebeurt hetzelfde met een reëel getal B.

Laat "A" en "B" twee getallen op de echte lijn, de afstand die ze scheidt, is:

D_Aab = │b - a│

Die ook kan worden berekend door:

D_Aab = │a - b│

De afstand tussen a = 5 en b = 12 is bijvoorbeeld:

D = │5−12│ = │12−5│ = 7

Op deze manier is de absolute waarde van de aftrekking tussen twee reële getallen eenvoudigweg de afstand die ze op de echte lijn scheidt.

Absolute waardefunctie

De absolute waardefunctie is een toepassing die op de set reële getallen gaat ℛ tot ℛ⁺, die overeenkomt met elk reëel getal zijn absolute waarde. Het wordt gedefinieerd door:

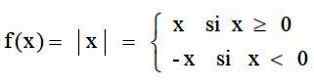
En de grafiek heeft de typische V -vorm:

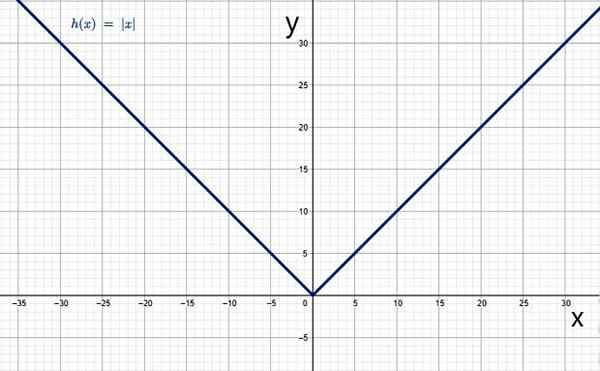De absolute waarde als functie. Bron: f. Zapata door Geogebra.

Kenmerken van de absolute waardefunctie

-Uw domein is de set van alle reële getallen.

-Het is continu.

-Het is zelfs, omdat het wordt vervuld dat f (x) = f (-x), daarom is de verticale as een symmetrieasas.

-Het bereik van de absolute waardefunctie is de set van positieve reële, inclusief 0, omdat de functie altijd een afstand vertegenwoordigt, en dit is altijd positief of nul.

Kan u van dienst zijn: wat is de richtlijn? (Geometrie)

-Het is een functie per secties of door onderdelen.

-Neemt af in het interval (-∞, 0) en groeit in (0,+∞).

Het argument van absolute waarde kan ook een kwadratische of andere functie zijn, het kan bijvoorbeeld worden gedefinieerd:

• f (x) = │x²-5x+3│
• g (x) = │sen x│

De absolute waarde is verantwoordelijk om positief te worden, de beelden van het argument die een negatief teken hebben.

Opgeloste oefeningen

Oefening 1

Evalueer de volgende algebraïsche uitdrukkingen met absolute waarde:

a) │2x - 5│ + │ --x + 1│ at x = 3

b) │ (x - 5) ÷ (x+4) │ op x = −1

Oplossing voor

│2⋅3−5│ + │ - 3 + 1│ = │6−5│ + │ - 2│ = │1│ + 2 = 3

Oplossing B

│ (−1−5) ÷ (−1+4) │ = │ (−6) ÷ (3) │ = │ - 2│ = 2

Oefening 2

Wat is de set van waarden die de volgende ongelijkheid vertegenwoordigt?

│x│≤ 3

Oplossing

Ongelijkheid vertegenwoordigt alle reële getallen waarvan de absolute waarde kleiner is dan of gelijk is aan 3, daarom is het de set van alle getallen tussen -3 en +3, inclusief deze.

In de intervalnotatie blijft het:

[-3,3]

Oefening 3

Los de volgende vergelijking op met absolute waarde:

│2x-1│ = 5

Oplossing 

Zoals eerder aangegeven, om een ​​vergelijking met absolute waarde op te lossen, is het noodzakelijk om de twee opties te overwegen. Ik bedoel ja:

│f (x) │ = c

Dus:

1) f (x) = c

2) f (x) = -c

Daarom heeft deze vergelijking, waarvan het argument lineair is, twee oplossingen:

Eerste oplossing

2x - 1 = 5

2x = 6 ⇒ x₁ = 3

Tweede oplossing

2x - 1 = -5

2x = -4 ⇒ x₂ = -2

Bij het evalueren van x₁ = 3 of x₂ = -2 In de oorspronkelijke vergelijking moet een gelijkheid worden verkregen, op deze manier wordt geverifieerd dat de verkregen waarden oplossing zijn van de voorgestelde vergelijking. Inderdaad:

│ (2⋅3) -1│ = │6-1│ = 5

En wanneer u met de tweede optie probeert, wordt ook een gelijkheid verkregen:

│2⋅ (-2) -1│ = │-4-1│ = 5

Referenties

1. Baldor, een. 2005. Algebra. Culturele thuislandgroep.
2. Larson, r. 2012. Voorzetting. 8e. Editie. Cengage leren.
3. Hoffman, J. Selectie van wiskundeproblemen. Deel 2.
4. Stewart, J. 2007. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
5. Zill, D. 1984. Algebra en trigonometrie. McGraw Hill.