Frequentieverdeling hoe een tabel te maken, bijvoorbeeld, oefening

A Frequentieverdeling In statistieken verwijst het naar de trend die volgt op de gegevens die zijn georganiseerd in groepen, categorieën of klassen, wanneer elk een nummer wordt toegewezen dat frequentie wordt genoemd, wat aangeeft hoeveel gegevens er in elke groep zijn. 

In de regel wordt opgemerkt dat deze frequenties worden verdeeld over een centrale groep: degene met het hoogste aantal gegevens.

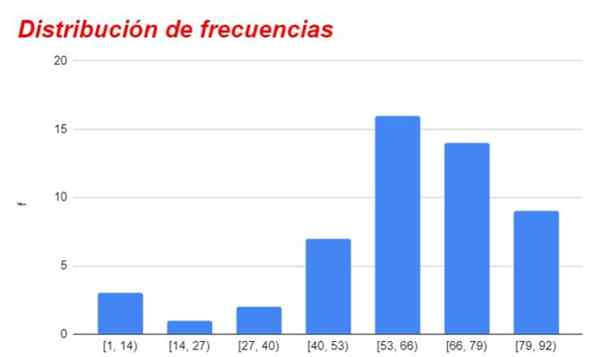
Figuur 1. Frequentiedistributiekaart verkregen uit de overeenkomstige tabel. Bron: f. Zapata.

Groepen die boven of onder de genoemde centrale categorie zijn, verlaagt geleidelijk hun frequentie, die erg klein of onbeduidend zijn voor de categorieën het verst van de categorie met een hogere frequentie.

De manier om de frequentieverdeling van een gegevensset te kennen, bestaat eerst uit het maken van de categorieën en vervolgens de frequentietabel maken. De visuele weergave van de frequentietabel wordt histogram genoemd.

[TOC]

Frequentietypen

Er zijn verschillende soorten frequenties:

1.- Absolute frecuency: Het is de meest basale, en daaruit zijn de anderen gebouwd. Het bestaat eenvoudig uit het totale aantal gegevens dat overeenkomt met een categorie.

2.- Relatieve frequentie: Het is de absolute frequentie van elke categorie gedeeld door het totale aantal gegevens.

3.- Percentagefrequentie: Het is dezelfde relatieve frequentie maar vermenigvuldigd met honderd, wat het percentage van de verschijning van de waarden in elke categorie aangeeft.

4.- Opgebouwde frequentie: Het is de som van de absolute frequenties van de categorieën lager of gelijk aan de categorie die wordt overwogen. 

5.- Percentage geaccumuleerde frequentie: Het is de som van de procentuele frequenties van de categorieën lager of gelijk aan de categorie die wordt waargenomen.

Stappen om een ​​frequentieverdelingstabel te maken

Er zijn verschillende stappen te volgen om een ​​frequentieverdelingstabel te bouwen.

In de eerste plaats moeten de gegevens van een boom, enz.

Kan u van dienst zijn: wat zijn de delers van 30? (Uitleg)

Stap 1

Identificeer de minimumwaarde Xmin en de maximale waarde Xmax In de gegevensset X.

Stap 2

Bereken het R -bereik, dat wordt gedefinieerd als het verschil tussen de maximale waarde minder de minimale waarde: r = xmax - xmin.

Stap 3

Bepaal het nummer k van intervallen of klassen, die vooraf kunnen worden ingesteld. Het nummer k zal het aantal rijen bepalen dat de frequentietabel zal hebben.

Stap 4

In het geval het aantal intervallen k Het wordt niet eerder gegeven, dan moet het worden vastgesteld volgens de volgende richtlijnen: het minst aantal aanbevolen categorieën is 5, maar het kan hoger zijn, in welk geval het de voorkeur heeft om een ​​oneven nummer te kiezen.

Stap 5

Er is een formule genoemd Storgen regel Dat geeft ons het aantal intervallen k aanbevolen voor een set die uit bestaat N gegevens:

K = [1 + 3,322⋅log n]

Als het resultaat binnen de beugel zal zeker een reëel getal zijn, geeft de beugel aan dat deze moet worden afgerond met het dichtstbijzijnde oneven geheel getal om een ​​geheel getal te verkrijgen k.

Stap 6

De amplitude wordt berekend NAAR van elk interval (klassen of categorieën) die het quotiënt tussen het bereik nemen R en het aantal intervallen k: A = r/k. Als de originele gegevens volledige getallen zijn, is het dichtstbijzijnde gehele getal afgerond, anders is de echte waarde overgelaten.

Stap 7

Bepaal de onderste en bovengrenzen van elk interval of klasse. Het eerste interval, of de laagste klasse, heeft als ondergrens de kleinste van de oorspronkelijke gegevens, dat wil zeggen Li = Xmin en als de bovengrens de minimale waarde plus de amplitude van het interval, dit is LS = Xmin + A. 

Stap 8

De opeenvolgende intervallen zijn: 

[[Xmin, xmin + a), [ Xmin + a, xmin + 2⋅a), ... [ Xmin + (K-1) A, Xmin + K⋅a)).

Kan u van dienst zijn: gecombineerde bewerkingen

Stap 9

Het XC -klassenmerk wordt voor elk interval bepaald met behulp van de volgende formule: Xc = (ls - li) / 2 + li.

Stap 10

De koers van de frequentietabel is geplaatst, die bestaat uit een rij met de volgende labels: klassen, XC Class -merk, frequentie F, relatieve frequentie F (of percentagefrequentie F%) en geaccumuleerde frequentie F (of geaccumuleerde procentuele frequentie F%).

Wat we hierna zullen hebben, is de volgende:

Eerste kolom van de frequentietabel: bevat de intervallen of klassen waarin de gegevens zijn verdeeld.

Tweede kolom: bevat het klassenmerk (of tussenliggende punt) van elke subinterval.

Derde kolom: Bevat de absolute frequentie F van elke klasse of categorie.

Vierde en vijfde kolom: De waarden die overeenkomen met de relatieve (of percentage) frequentie en de geaccumuleerde frequentie F (of percentage geaccumuleerd) worden geplaatst.

Voorbeeld van tabelconstructie

De volgende gegevens komen overeen met de nauwkeurige antwoorden van 100 vragen die zijn toegepast op een groep van 52 studenten:

65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.

We zullen de stappen volgen om de frequentietabel te bouwen:

1.- Minimale en maximale waarden xmin = 1, xmax = 89.

2.- Het bereik is: r = 89 - 1 = 88

3.- Bepaling van het aantal intervallen volgens de Storgen regel: K = [1 + 3,322⋅log 52] = [6,70] = 7.

4.- Berekening van de breedte van de intervallen: a = r / k = 88/7 = 12.57 ≈ 13.

5.- De intervallen zijn: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92).

6.- De klassenmerken van elk interval worden bepaald: 8, 21, 34, 47, 60, 73 en 86.

7.- De tabel is gemaakt:

Kan u van dienst zijn: interne en externe conjugaathoeken: voorbeelden, oefeningen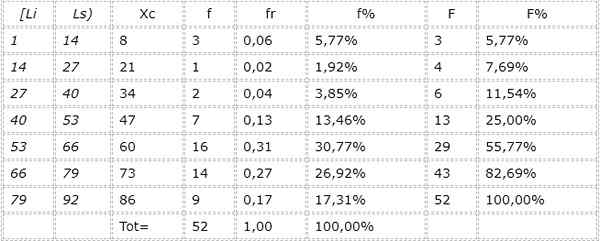

De grafiek van de frequenties voor de verschillende intervallen of categorieën wordt weergegeven in figuur 1.

Oefening opgelost

Een leraar registreert het percentage van de doelstellingen die zijn bereikt in het onderwerp natuurkunde voor elke student. De kwalificatie voor elke student, hoewel deze afhangt van het percentage van de doelstellingen, is echter krap in bepaalde categorieën die eerder zijn vastgesteld in de voorschriften van de University Studies.

Laten we eens kijken naar een specifiek geval: in een fysica -sectie heb je het percentage van de doelstellingen voor elk van de 52 studenten: 

15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61, 61. 65, 70, 89, 64, 54, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.

In dit voorbeeld komen de categorieën of klassen overeen met de uiteindelijke kwalificatie die is toegewezen volgens het percentage X van de bereikte doelstellingen:

1.- Zeer slecht: 1 ≤ x < 30

2.- Slecht: 30 ≤ x < 50

3.- Genoeg: 50 ≤ x < 70

4.- Nou: 70 ≤ x < 85

5.- Uitstekend: 85 ≤ x ≤ 100

Om de frequentietabel te maken, worden de gegevens van het minst tot het grootst besteld en vertelt hoeveel gegevens overeenkomen met elke categorie, wat de kwalificatie zal zijn die de student zal verkrijgen in het onderwerp natuurkunde:

1.- Zeer slecht: 4 studenten.

2.- Slecht: 6 studenten.

3.- Genoeg: 20 studenten.

4.- Nou: 17 studenten.

5.- Uitstekend: 5 studenten.

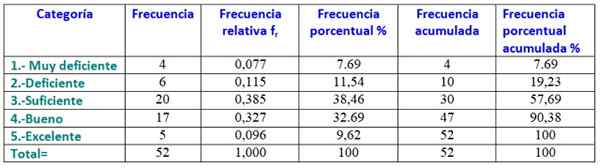
Hieronder is het histogram van de cijfers, gebouwd uit de vorige tabel:

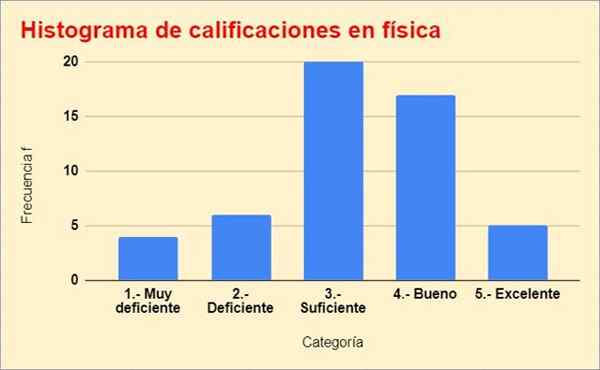Figuur 2. Frequentieverdelingsgrafiek van de oefening opgelost. Bron: f. Zapata.

Referenties

1. Berenson, m. 1985. Statistieken voor administratie en economie. Inter -American S.NAAR.
2. Canavos, G. 1988. Waarschijnlijkheid en statistieken: toepassingen en methoden. McGraw Hill.
3. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
4. Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.
5. Spiegel, m. 2009. Statistieken. Schaum -serie. 4 TA. Editie. McGraw Hill.
6. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.