Fourier -serie toepassingen, voorbeelden en oefeningen opgelost

De Fourier -serie Ze bestaan ​​uit een som van oneindige termen, die bestaan ​​uit harmonische functies, sinus en cosinus, wiens argument een hele fundamenteel is voor een fundamentele frequentie.

De sinus- en cosinusfuncties worden vermenigvuldigd met waardencoëfficiënten, zodat de som identiek is aan een functie met periode t gelijk aan tweemaal pi (2π) gedeeld door de fundamentele hoekfrequentie ω ω.

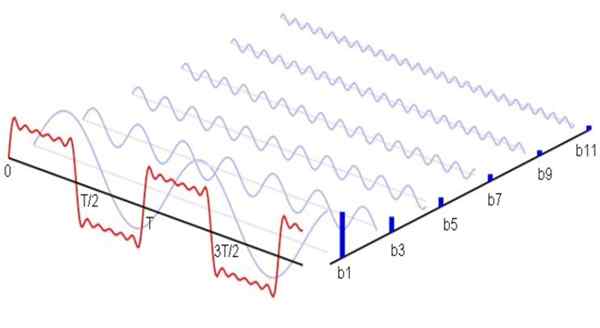
Figuur 1. Hier zijn (in blauw) de eerste niet -nulharmonischen van de Fourier -serie die overeenkomt met een vierkant golfvormsignaal. De som die deze harmonischen aanleiding geven tot het rode signaal. Bron: Wikimedia Commons.

Wiskundig zou het als volgt worden uitgedrukt: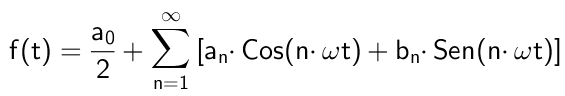

Waar Ω Het is de fundamentele frequentie, die verband houdt met de periode T van de functie F (t) Door de relatie: 

Ω = 2π / t

Voor het zijn van periodieke periode T, de functie F (t) voldoet aan deze voorwaarde:

f (t) = f (t + k t)

Waar k Het is een geheel getal en de coëfficiënten₀ , naar_N en B_N Ze worden de Fourier -coëfficiënten.

[TOC]

Belang en gebruik van Fourier -serie

De naam van Fourier -serie is te wijten aan het feit dat zijn ontdekker de Franse wiskundige was.

Deze ontdekking was fundamenteel voor de wiskunde, omdat als een differentiaalvergelijking een bepaalde harmonische oplossing heeft, het mogelijk is om de algemene oplossing te bereiken door middel van de overlap of som van hetzelfde.

Fourier's coëfficiënten van een periodieke functie, ook wel genoemd teken, Ze zijn het spectrum van hetzelfde.

Daarom is het spectrum de set frequenties die een signaal vormen dat wordt gekenmerkt door de amplitude van elke frequentie, wat overeenkomt met de waarden van Fourier's coëfficiënten.

Signaalcompressiesystemen of audio- en videogolfvormen, aan de achterkant aanzienlijk kleiner aantal bits dan het oorspronkelijke gedigitaliseerde signaal.

De Fourier -serie van een signaal is als zijn vingerafdruk, in de zin dat, bekend de coëfficiënten die het vormen, je altijd kunt weten welk teken ze erbij horen.

Hoewel het gebruik van de Fourier -serie, of de meest algemene vorm, de Fourier -transformatie, Als een signaalcompressiemethode is het al geruime tijd bekend, het gebruik ervan in de praktijk moest wachten op numerieke processors snel genoeg, waardoor de signalen konden worden gecomprimeerd en gedecomprimeerd in "realtime".

Kan u van dienst zijn: statistische variabelen

Fourier -serie voorbeeld 

Vervolgens een voorbeeld van F (T) -functie en de Fourier -serie.

De functie is:

 f (t) = 0 ja 0 ≤ t  < π y 1 si π ≤  t   < 2π

En heeft zijn bijbehorende Fourier -serie gegeven door:

f (t) = ½ - 2/π⋅SE (t) - 2/(3π) ⋅SE (3T) - 2/(5π) ⋅sen (5t) - 2/(7π) ⋅sen (7t) -…

De volgende figuur toont de functie en gedeeltelijke som van de Fourier -serie:

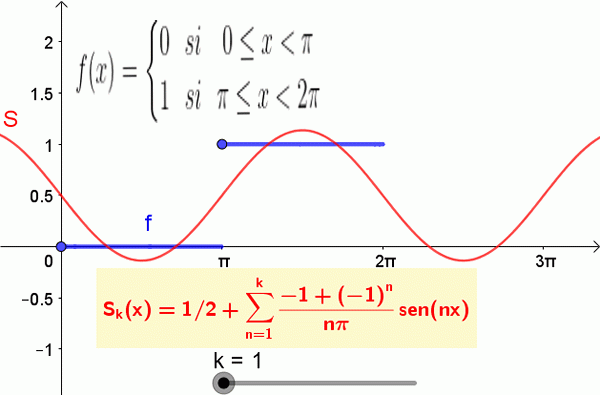Figuur 2. De eerste 19 termen van de som van Fourier die overeenkomen met de stapfunctie worden getoond. Bron: f. Zapata.

Bepaling van coëfficiënten

Hieronder vindt u hoe u de coëfficiënten van Fourier kunt bepalen:

Stel dat de functie f (x) is gedefinieerd in een interval dat van t gaat_Je tot t_Je + T, waar kapitaal de periode van de functie zal zijn. Dan is zijn Fourier -serie:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 Ω t) +… + a_N Cos (n ω t) +..

.. .+ b₁ sin (ω t) +b₂ sin (2 ω t) +… +b_N Sin (n ω t) +..

Berekening van de onafhankelijke termijn

Om de onafhankelijke term te vinden, integreren we beide leden van gelijkheid in het interval van de definitie van de functie:

[T_Je , T_Je+ T]

Daarom:

Dezelfde_N ∫cos (n ω t) dt +..

.. .+ b₁ ∫sen (ω t) dt +b₂ ∫sen (2 Ω t) dt +… +b_N ∫sen (n ω t) dt +..

Hier betekent het symbool ∫ integraal gedefinieerd uit t_Je tot t_Je + T.

De integrale van de eerste term is t, die wanneer geëvalueerd in de bovengrensresultaten:

T_Je + T

Bij het aftrekken van de ondergrens T_Je, in definitieve t.

Alle andere termen zijn 0, omdat dit cosinus- of sinusfuncties zijn die in een volledige periode worden geëvalueerd, zoals we hieronder laten zien:

∫cos (nω t) dt = (1/ nω) ∫cos (nω t) d (nω t)

Onthoud dat het symbool ∫ integratie betekent tussen t_Je tot t_Je + T. 

Om de integratie van de termen die cosinus of borst hebben te maken, zullen we de volgende wijziging van variabele aanbrengen:

x = ω (t - t_Je))

Dus het x, dx differentieel is gelijk aan het differentieel d (ωt).

Dus de integraal om uit te voeren is:

Omdat n een geheel getal is, zal de gedefinieerde integrale altijd nul geven. Hetzelfde geldt voor de sinusfunctie.

Daarom bevat de gedefinieerde integraal geëvalueerd in een volledige periode van alle voorwaarden. 

Kan u van dienst zijn: divisies waarin het residu 300 is

Daarom wordt geconcludeerd dat de term A₀ als volgt wordt berekend:

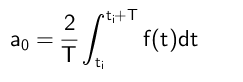
Berekening van coëfficiënten

Om de coëfficiënten te berekenen die zich vermenigvuldigen met de cosinusfuncties, moeten beide leden van gelijkheid worden vermenigvuldigd:

f (t) = a₀/2 + a₁ cos (ω t) + a₂ cos (2 Ω t) +… + a_N Cos (n ω t) +..

.. .+ b₁ sin (ω t) +b₂ sin (2 ω t) +… +b_N Sin (n ω t) +..

Door de cosinusfunctie geëvalueerd in de overeenkomstige harmonische en vervolgens wordt de integraal gedefinieerd in een volledige periode op beide leden toegepast. 

Bijvoorbeeld om te berekenen_M Beide leden worden vermenigvuldigd met COS (MωT):

f (t) cos (m ω t) = a₀/2 cos (m ω t) + a₁ cos (ω t) cos (m ω t) + a₂ cos (2 ω t) cos (m ω t) +… + naar_N Cos (n ω t) cos (m ω t) +..

.. .+ b₁ sin (ω t) cos (m ω t) +b₂ sin (2 ω t) cos (m ω t) +… +b_N Sin (n ω t) cos (m ω t) +..

Integreer vervolgens in een volledige periode, dat wil zeggen in het interval dat van t gaat_Je tot t_Je + T.

De integrale van de term die A₀ bevat, is geannuleerd, omdat M een geheel getal is en de cosinusfunctie wordt geïntegreerd in een volledige periode. 

Integralen die de productcos (n ω t) cos (m ω t) bevatten, worden ook geannuleerd wanneer n ≠ m. Alleen in het geval dat N = M de integraal heeft:

Alle termen met een cosinus vermenigvuldigde sinus, dat wil zeggen die die worden vermenigvuldigd door de B's coëfficiënten, omdat het bevatten periode. 

Vanaf hier wordt geconcludeerd dat:

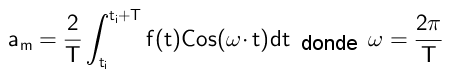
Berekening van de coëfficiënten B's

Om de B -coëfficiënten van B te vinden, wordt een vergelijkbare procedure toegepast, maar deze keer worden beide leden van de functie die overeenkomt met de Fourier -serie vermenigvuldigd met de SEN -functie (M ω T).

Om dezelfde redenen die al zijn uitgelegd voor de zaak waarin de enige term die niet wordt geannuleerd na de integratie in een volledige periode, is er een waarin:

n = m

En waar de integrale van [sen (m ω t)] verschijnt]², die geïntegreerd in een volledige periode resulteert in π.

Kan u van dienst zijn: homografische functie: hoe u kunt grafieken, opgeloste oefeningen

Op deze manier worden de coëfficiënten van de B berekend volgens de volgende formule:

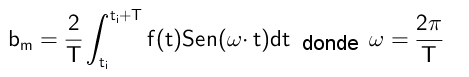
Opdrachten

- Oefening 1

Maak de expliciete berekening van de coëfficiënten van de functie

 f (t) = 0 ja 0 ≤ t  < π y 1 si π ≤  t   < 2π

Oplossing

Eerst identificeren we de periode T van deze functie als 2π, dus de fundamentele frequentie ω = 2π/ t in dit voorbeeld is gelijk aan de eenheid, dat wil zeggen:

Ω = 1

De functie is gedefinieerd in het interval [0, 2π], dus alle integraties zullen in genoemde interval worden uitgevoerd. 

Dan wordt de onafhankelijke term als volgt berekend:

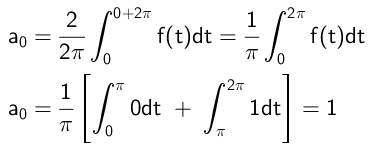
De coëfficiënten die zich vermenigvuldigen met de cosinusfuncties worden op deze manier berekend:

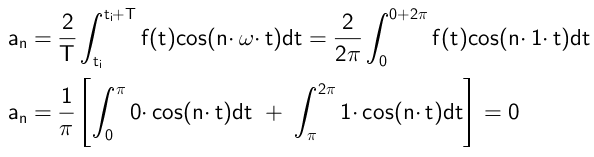
Zoals te zien is, zijn alle coëfficiënten tot nul, wat zal gebeuren op voorwaarde dat de functie f (t) vreemd is.

Evenzo zullen de B -coëfficiënten als volgt worden berekend:

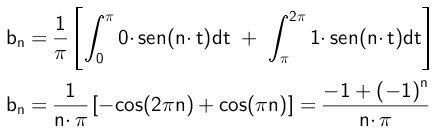
- Oefening 2

Zoek de coëfficiënten van de functie die overeenkomt met figuur 1, dat is:

f (t) = -1 ja 0≤ t

Oplossing 

Aangezien de functie waarden tussen -1 en +1 nodig heeft, kunnen we intuïteren dat de onafhankelijke term nietig is, maar we zullen deze expliciet berekenen:

Vanwege het feit dat de functie vreemde symmetrie heeft, moeten alle coëfficiënten die de harmonische termen vermenigvuldigen met de cosinusfunctie, nietig zijn. We verifiëren het hieronder:

Ten slotte zullen we de coëfficiënten van de B vinden die de harmonische termen vermenigvuldigen die de sinusfunctie bevatten:

Waar kunnen alle voorwaarden van B's Subscript worden opgemerkt, zijn 0. De eerste vreemde termen zijn:

B₁= -4/(π); B₃= -4/(3π); B₅= -4/(5π); B₇= -4/(7π) en B₉= -4/(9π)

https: // youtu.Be/737yagwszya

Referenties

1. Amerror, ik. 2013. De discrete Fourier -transformatie beheersen in één, twee of meerdere dimensies: valkuilen en artefacten. Springer Science & Business Media.
2. Briggs, W. negentienvijfennegentig. De DFT: een handleiding van een eigenaren voor de discrete Fourier -transformatie. Siam.
3. Chu, E. 2008. Discrete en continue Fourier -transformaties: analyse, toepassingen en snelle algoritmen. CRC Press.
4. Guoan Bi, Yonghong Zeng. 2012. Transformeert en snelle algoritmen voor signaalanalyse en representaties. Springer Science & Business Media.
5. Sundararajan, D. 2003. Digitale signaalverwerking: theorie en praktijk.Wereldwetenschappelijk. 
6. Wikipedia. Fourier -serie. Hersteld van: is.Wikipedia.com