Lineaire dilatatie wat is, formule en coëfficiënten, voorbeeld

De Lineaire verwijding treedt op wanneer een object dilatatie ervaart vanwege een temperatuurvariatie, voornamelijk in een enkele dimensie. Dit komt door de kenmerken van het materiaal of de geometrische vorm. 

Bijvoorbeeld, in een draad of in een balk, wanneer een toename van de temperatuur is, is de lange temperatuur die de grootste verandering lijdt vanwege thermische verwijding.

Vogels gesteld in draden. Bron: Pixabay.

De kabels waarin de vogels van de vorige figuur een stuk lijden wanneer hun temperatuur stijgt; In plaats daarvan samentrekken ze als ze afkoelen. Op dezelfde manier gebeurt het bijvoorbeeld met de staven die de rails van een spoorweg vormen.

[TOC]

Wat is lineaire verwijding?

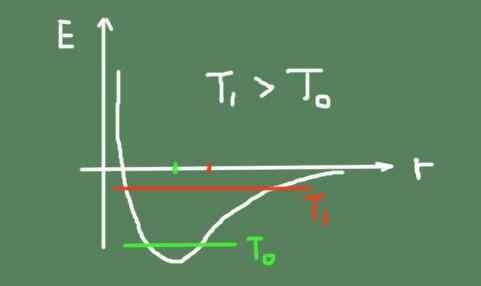Grafiek van de energie van de chemische binding versus de interatomische afstand. Bron: zelf gemaakt.

In een vast materiaal behouden atomen hun relatieve posities min of meer gefixeerd rond een balanspunt. Vanwege thermische agitatie oscilleren ze er echter altijd omheen.

Door de temperatuur te verhogen, neemt ook de thermische oscillatie toe, waardoor gemiddelde oscillatieposities veranderen. Dit komt omdat het linkpotentieel niet bepaald parabolisch is en asymmetrie heeft rond het minimum.

Hieronder staat een figuur dat de energie van de chemische binding schetst, afhankelijk van de interatomaire afstand. De totale oscillatie -energie bij twee temperaturen wordt ook getoond, en hoe het oscillatiecentrum beweegt.

Formule van lineaire verwijding en de coëfficiënt ervan

Om de lineaire verwijding te meten, beginnen we met een initiële LE -lengte en een begintemperatuur T, van het object waarvan u uw dilatatie wilt meten.

Stel dat dit object een balk is waarvan de lengte L is en de afmetingen van de dwarsdoorsnede veel lager zijn dan L.

Kan u van dienst zijn: onmiddellijke versnelling: wat is het, hoe het wordt berekend en oefeningen

Ten eerste wordt dit object onderworpen aan een AT -temperatuurvariatie, zodat de eindtemperatuur van het object zodra het warmte -evenwicht is vastgesteld met de warmtebron T '= T+ Δt zal zijn.

Tijdens dit proces is de lengte van het object ook gewijzigd in een nieuwe waarde l '= l + Δl, waarbij Δl de variatie van de lengte is.

De lineaire dilatatiecoëfficiënt α wordt gedefinieerd als de verhouding tussen de relatieve variatie van lengte per eenheid van temperatuurvariatie. De volgende formule definieert de lineaire dilatatiecoëfficiënt α:

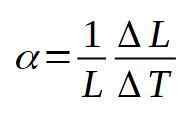In de meeste gevallen, α Het heeft een constante waarde voor temperaturen tussen (t - Δt) en (t + Δt).

De afmetingen van de lineaire dilatatiecoëfficiënt zijn die van temperatuur.

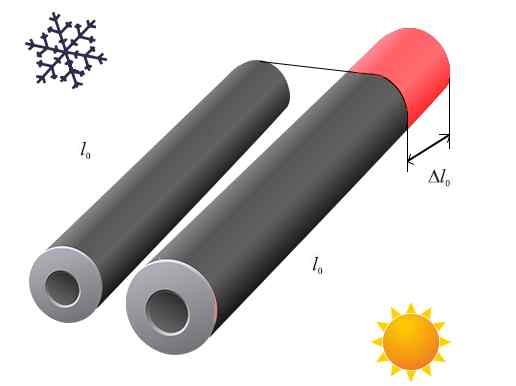
De temperatuur verhoogt de lengte van buisvormige vaste stoffen. Dit is wat bekend staat als lineaire verwijding. Bron: Lafer.com

Lineaire dilatatiecoëfficiënt voor verschillende materialen

Vervolgens geven we een lijst met de lineaire dilatatiecoëfficiënt voor sommige typische materialen en elementen. De coëfficiënt wordt berekend in normale atmosferische druk op basis van een omgevingstemperatuur van 25 ° C; en de waarde ervan wordt als constant beschouwd in een bereik van AT tot 100 ° C.

De lineaire dilatatiecoëfficiëntseenheid is (° C)^-1.

- Staal: α = 12 ∙ 10^-6 (° C)^-1

- Aluminium: α = 23 ∙ 10^-6 (° C)^-1

- Goud: α = 14 ∙ 10^-6 (° C)^-1

- Koper: α = 17 ∙ 10^-6 (° C)^-1

- Messing: α = 18 ∙ 10^-6 (° C)^-1

- IJzer: α = 12 ∙ 10^-6 (° C)^-1

- Glas: α = (7 tot 9) ∙ 10^-6 (° C)^-1

- Kwik: α = 60,4 ∙ 10^-6 (° C)^-1

- Kwarts: α = 0,4 ∙ 10^-6 (° C)^-1

- Diamant: α = 1,2 ∙ 10^-6 (° C)^-1

- Lood: α = 30 ∙ 10^-6 (° C)^-1

Het kan u van dienst zijn: convectiewarmteoverdracht (met voorbeelden)

- Eiken hout: α = 54 ∙ 10^-6 (° C)^-1

- PVC: α = 52 ∙ 10^-6 (° C)^-1

- Koolstofvezel: α = -0.8 ∙ 10^-6 (° C)^-1

- Beton: α = (8 tot 12) ∙ 10^-6 (° C)^-1

De meeste materialen strekken zich uit met een temperatuurstijging. Sommige speciale materialen zoals koolstofvezel krimpen echter met de temperatuurstijging.

Opgeloste voorbeelden van lineaire expansie

voorbeeld 1

Een koperen kabel wordt opgehangen tussen twee palen, en de lengte in een koele dag bij 20 ° C is 12 m. Bereken de waarde van zijn lengte op een warme dag bij 35 ° C.

Oplossing

Beginnend met de definitie van de lineaire dilatatiecoëfficiënt en weten dat voor koper deze coëfficiënt waard is: α = 17 ∙ 10^-6 (° C)^-1

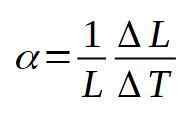
De toename van de lengte wordt gegeven door: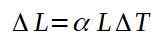

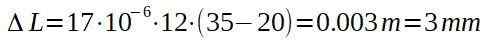
De koperen kabel ondergaat een toename van zijn lengte, maar dit is slechts 3 mm. Dat wil zeggen, de kabel gaat van 12.000 m naar 12.003 m.

Voorbeeld 2

In een smidse verlaat een aluminium staaf de oven op 800 graden Celsius, met een lengte van 10,00 m. Zodra het afkoelt tot de omgevingstemperatuur van 18 graden Celsius, bepaalt u de lengte die de balk zal hebben.

Oplossing

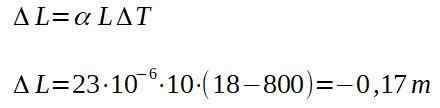
Dat wil zeggen dat de bar, eenmaal koud, een totale lengte zal hebben van:

9,83 m.

Voorbeeld 3

Een stalen klinknagel heeft een diameter van 0.915 cm. Een gat van 0,910 cm wordt gemaakt op een aluminiumplaat. Dit zijn de initiële diameters wanneer de omgevingstemperatuur 18 ° C is.

Bij welke minimumtemperatuur moet de plaat worden verwarmd zodat de klinknagel door het gat gaat? Het doel hiervan is dat wanneer het ijzer terugkeert naar kamertemperatuur, de klinknagel op de plaat wordt aangepast.

Kan u van dienst zijn: Parallellogram -methode: voorbeelden, opgeloste oefeningen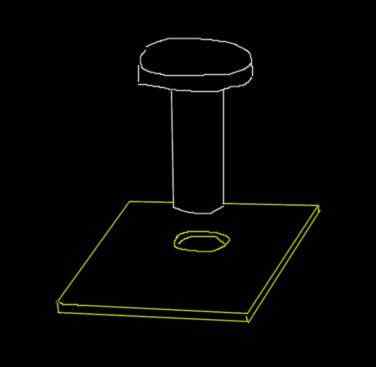Figuur bijvoorbeeld 3. Bron: zelf gemaakt.

Oplossing

Hoewel de plaat een gebied is, zijn we geïnteresseerd in dilatatie van de gatdiameter, wat een dimensionale hoeveelheid is.

Laten we bellen₀ naar de oorspronkelijke diameter van de aluminiumplaat en D die eenmaal verwarmd zal zijn.

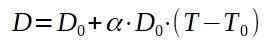
Je hebt de eindtemperatuur op, je hebt:

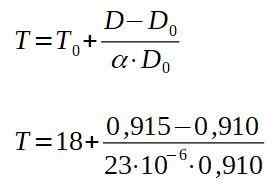
Het resultaat van de vorige bewerkingen is 257 ° C, wat de minimumtemperatuur is waarbij de plaat moet worden verwarmd zodat de klinknagel door het gat gaat.

Voorbeeld 4

De klinknagel en plaquette van de vorige oefening worden in een oven samengebracht. Bepaal bij welke minimale temperatuur de oven moet zijn zodat de stalen klinknagel door het aluminium plaatgat gaat.

Oplossing

In dit geval zullen zowel de klinknagel als het gat vertragen. Maar de stalen dilatatiecoëfficiënt is α = 12 ∙ 10^-6 (° C)^-1, Terwijl het aluminium α = 23 ∙ 10 is^-6 (° C)^-1 .

We zoeken dan naar een eindtemperatuur T zodanig dat beide diameters samenvallen.

Als we 1 naar de klinknagel bellen en 2 op de aluminiumplaat, zoeken we naar een eindtemperatuur t zodanig dat D₁ = D₂.

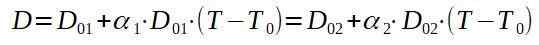
Als we de eindtemperatuur t wissen, hebben we:

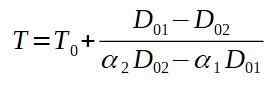
Vervolgens plaatsen we de overeenkomstige waarden.

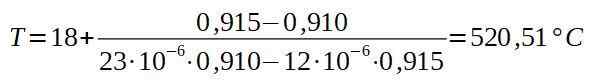
De conclusie is dat de oven ten minste 520,5 ° C moet zijn, zodat de klinknagel door het aluminium plaatgat gaat.

Referenties

1. Giancoli, D.  2006. Fysica: principes met toepassingen. Zesde editie. Prentice Hall. 238-249.
2. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. Mac Graw Hill. 422-527.