Verschil in formules, vergelijkingen, voorbeelden, oefeningen

De Verschil van kubussen Het is een binomiale algebraïsche uitdrukking van de vorm³ - B³, waar termen A en B reële getallen of algebraïsche uitdrukkingen van verschillende typen kunnen zijn. Een voorbeeld van Cubes -verschil is: 8 - x³, Omdat 8 kan worden geschreven als 2³.

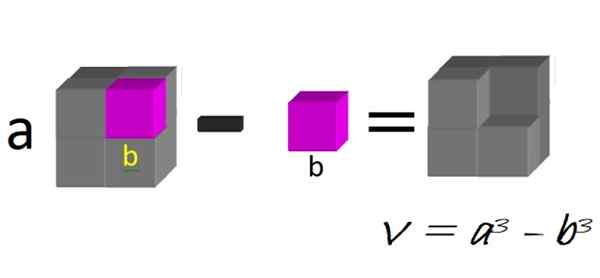
Geometrisch kunnen we een grote kubus bedenken, van zijde A, waaraan de kleine bube van zij B wordt afgetrokken, zoals geïllustreerd in figuur 1:

Figuur 1. Een verschil met blokjes. Bron: f. Zapata.

Het volume van de resulterende figuur is precies een verschil in kubussen:

V = a³ - B³

Om een ​​alternatieve uitdrukking te vinden, wordt waargenomen dat deze figuur kan worden opgesplitst in drie prisma's, zoals hieronder getoond:

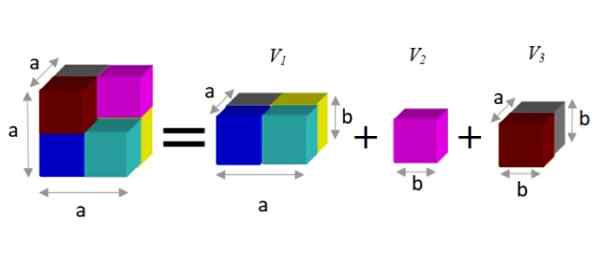Figuur 2. Het verschil in kubussen (links van gelijkheid) is gelijk aan de som van gedeeltelijke volumes (rechts). Bron: f. Zapata.

Een prisma heeft een volume gegeven door het product van zijn drie dimensies: Breedte x Hoge x Diepte. Op deze manier is het resulterende volume:

V = a³ - B³ = A².B + B³ + naar.B²

De factor B Het is aan de rechterkant. Bovendien wordt in de hierboven getoonde figuur met name vervuld dat:

b = (a/2) ⇒ a = b + b

Daarom kan worden gezegd dat: b = a - b. Dus:

naar³ - B³ = B (a² + B² +naar.b) = (a-b) (a² + naar.B + B²))

Deze manier om het verschil in kubussen uit te drukken zal in veel toepassingen zeer nuttig blijken te zijn en zou op dezelfde manier zijn verkregen, hoewel de ontbrekende kubuszijde in de hoek verschilde van B = A/2.

Merk op dat de tweede haakjesHet lijkt veel naar het opmerkelijke product van het kwadraat van de som, maar de gekruiste term wordt niet vermenigvuldigd met 2. De lezer kan de rechterkant ontwikkelen om te controleren of deze effectief is verkregen naar³ - B³.

[TOC]

Kan u van dienst zijn: Square Binomial

Voorbeelden

Er zijn verschillende kubussenverschillen:

1 - m⁶

naar⁶B³ - 8z¹²En⁶

(1/125).X⁶ - 27.En⁹

Laten we elk van hen analiseren. In het eerste voorbeeld kan de 1 worden geschreven als 1 = 1³ en de term m⁶ Het blijft: (m²))³. Beide termen zijn perfecte kubussen, daarom is hun verschil:

1 -m⁶ = 1³ - (M²))³

In het tweede voorbeeld worden de termen herschreven:

naar⁶B³ = (a²B)³

8z¹²En⁶ = 2³ (z⁴))³ (En²))³ = (2z⁴En²))³

Het verschil van deze kubussen is: (a²B)³ - (2z⁴En²))³.

Ten slotte is de fractie (1/125) (1/5³), X⁶ = (x²))³, 27 = 3³ en en⁹ = (en³))³. Het vervangt dit alles in de oorspronkelijke uitdrukking, het wordt verkregen:

(1/125).X⁶  - 27y⁹ = [(1/5) (x²)]³ - (3y³))³

Factorisatie van een kubusverschil

Feit het verschil in kubussen vereenvoudigt veel algebraïsche bewerkingen. Om dit te doen, is het voldoende om de eerder afgetrokken formule te gebruiken:

figuur 3. Factorisatie van het verschil in blokjes en expressie van een opmerkelijk quotiënt. Bron: f. Zapata.

Nu bestaat de procedure om deze formule toe te passen drie stappen:

- Ten eerste wordt de kubieke wortel van elk van de termen van het verschil verkregen.

- Dan zijn de binomiale en trinomiale die aan de rechterkant van de formule verschijnen gebouwd.

- Ten slotte worden de binomiale en trinomiale vervangen om de uiteindelijke factorisatie te verkrijgen.

We zullen het gebruik van deze stappen illustreren bij elk van de voorbeelden van het hierboven voorgestelde verschil van kubussen en dus het gefactoriseerde equivalent verkrijgen.

voorbeeld 1

Feitieve uitdrukking 1 -m⁶   Volg de beschreven stappen. We beginnen met het herschrijven van de uitdrukking als 1 -m⁶ = 1³ - (M²))³ Om de respectieve kubieke wortels van elke term te extraheren:

Dan worden de binomiale en trinomiale gebouwd:

Het kan u van dienst zijn: wachtrijtheorie: geschiedenis, model, waarvoor is het voor en voorbeelden voor

A = 1

b = m²

Dus:

A - B = 1 - M²

 (naar² +naar.B + B²) = 1² + 1.M² + (M²))² = 1 + m² + M⁴

 Eindelijk wordt het vervangen in formule a³ - B³ = (a-b) (a² +naar.B + B²):

1 -m⁶ = (1 - m²) (1 + m² + M⁴))

Voorbeeld 2

Factorize:

naar⁶B³ -8z¹²En⁶ = (a²B)³ - (2z⁴En²))³

Omdat dit perfecte kubussen zijn, zijn kubieke wortels onmiddellijk: a²B en 2Z⁴En², Van daaruit volgt dat:

- Binomiaal: a²B - 2z⁴En²

- Trinomial: (a²B)² + naar²B. 2z⁴En² + (naar²B +2Z⁴En²))²

 En nu is de gewenste factorisatie gebouwd:

naar⁶B³ -8z¹²En⁶ = (a²B - 2z⁴En²)). [(naar²B)² + naar²B. 2z⁴En² + (naar²B + 2Z⁴En²))²] =

= (a²B - 2z⁴En²)). [naar⁴B² + 2e²B.Z⁴En² + (naar²B + 2Z⁴En²))²]

In principe is de factorisatie gereed, maar het is vaak nodig om elke term te vereenvoudigen. Dan wordt het opmerkelijke product ontwikkeld vanuit een som - dat aan het einde verschijnt en vervolgens vergelijkbare termen toevoegt. Herinnerend dat het kwadraat van een som is:

(x + y)² = x² + 2xy + en²

Het opmerkelijke recht tot rechts ontwikkelt zich op deze manier:

(naar²B + 2Z⁴En²))² = A⁴B² + 4e²B.Z⁴En² + 4Z⁸En⁴

 Vervanging van de ontwikkeling die is verkregen bij de factorisatie van het verschil in kubussen:

naar⁶B³ -8z¹²En⁶ = (a²B - 2z⁴En²)). [naar⁴B² + 2e²B.Z⁴En² + naar⁴B² + 4e²B.Z⁴En² + 4Z⁸En⁴] =

Ten slotte wordt het groeperen van vergelijkbare termen en het factureren van de numerieke coëfficiënten, die allemaal paren zijn, het wordt verkregen:

(naar²B - 2z⁴En²)). [2e⁴B² + 6e²B.Z⁴En² + 4Z⁸En⁴] = 2 (a²B - 2z⁴En²)). [naar⁴B² + 3e²B.Z⁴En² + 2z⁸En⁴]

Voorbeeld 3

Factorize (1/125).X⁶  - 27y⁹ Het is veel eenvoudiger dan de vorige zaak. Eerst worden de equivalenten van A en B geïdentificeerd:

A = (1/5) x²

B = 3Y³

Vervolgens worden ze direct op de formule vervangen:

(1/125).X⁶  - 27y⁹ = [(1/5) x² - 3y³]. [(1/25) x⁴ + (3/5) x²En³ + 9y⁶]

Oefening opgelost

Het verschil in kubussen heeft, zoals we hebben gezegd, een verscheidenheid aan toepassingen in algebra. Laten we eens kijken:

Kan u van dienst zijn: 5 kenmerken van het Cartesiaanse vlak

Oefening 1

Los de volgende vergelijkingen op:

a) x⁵ - 125 x² = 0

b) 64 - 729 x³ = 0

Oplossing voor

Ten eerste is de vergelijking op deze manier een factor:

X² (X³ - 125) = 0

Omdat 125 een perfecte kubus is, wordt haakjes geschreven als een verschil in kubussen:

X² . (X³ - 5³) = 0

De eerste oplossing is x = 0, maar we vinden meer als we x maken³ - 5³ = 0, dan:

X³ = 5³ → x = 5

Oplossing B

De linkerkant van de vergelijking wordt herschreven als 64 - 729 x³ = 4³ - (9x)³. Daarom:

4³ - (9x)³ = 0

Omdat de exponent hetzelfde is:

9x = 4 → x = 9/4

Oefening 2

Factoriseer expressie:

(x + y)³ - (X - y)³

Oplossing

Deze uitdrukking is een verschil in kubussen, als we in de factor van de factorisatie opmerken dat:

A = x+ en

b = x- y

Dan wordt de binomiale eerst gebouwd:

a - b = x+ y - (x- y) = 2y

En nu het trinomiale:

naar² + naar.B + B² = (x+ y)² + (x + y) (x-y) + (x-y)²

Opmerkelijke producten worden ontwikkeld:

(x+ y)² = x² + 2xy +en²

(x+y) (x-y) = x²- En²

(x- y)² = x² - 2xy +en²

Dan moet u vergelijkbare termen vervangen en verminderen:

naar² + naar.B + B² = x² + 2xy +en²+ X²- En²+ X² - 2xy +en² = 3x² + En²

Factorisatieresultaten in:

(x + y)³ - (X - y)³ = 2y. (3x² + En²))

Referenties

1. Baldor, een. 1974. Algebra. Venezolaanse culturele redactionele s.NAAR.
2. CK-12 Foundation. Som en verschil van blokjes. Hersteld van: CK12.borg.
3. Khan Academy. Cubes verschilfactorisatie. Hersteld van: is.Khanacademy.borg.
4. Wiskunde is leuk gevorderd. Verschil van twee kubussen. Hersteld van: MathsisFun.com
5. UNAM. Factorisatie van een kubusverschil. Opgehaald uit: DCB.Fi-c.UNAM.mx.