Impliciete derivaten hoe ze worden opgelost en opgeloste oefeningen

De impliciete derivaten Het zijn tools die worden gebruikt in een differentiatietechniek die op functies wordt toegepast. Ze zijn van toepassing wanneer het niet mogelijk is, onder reguliere methoden, voert de opruiming van de afhankelijke variabele uit die moet worden afgeleid. Deze goedkeuring wordt gedaan op basis van de onafhankelijke variabele.

Bijvoorbeeld in de uitdrukking 3xy³ - 2y + xy² = xy, je kunt de uitdrukking niet krijgen die "y" definieert, afhankelijk van "x". Zodat wanneer de differentiële expressie dy/dx kan worden verkregen.

[TOC]

Hoe worden impliciete derivaten opgelost?

Om een ​​implicatie op te lossen, is het gebaseerd op een impliciete uitdrukking. Bijvoorbeeld: 3xy³ - 2y + xy² - Xy = 0. Dit is al duidelijk gewist, maar om dit te doen is geen noodzakelijke voorwaarde om de afgeleide van Y met betrekking tot X te verkrijgen. Vervolgens wordt elk van de elementen afgeleid met betrekking tot de kettingregel voor gemengde functies:

3xy³ Het bestaat uit 2 variabelen, daarom d (3xy³) Het zal worden behandeld als de afgeleide van een product van functies.

D (3xy³)/dx = 3y³ + 3y².(3x) en '= 3y³ + 9xy² En'

Waar het element en 'bekend staat als "en neef”En Dy/DX staat voor

-2y ontleent volgens wet K.U = k.OF'

D (-2y) = -2 en '

XY² veronderstelt een ander differentieel dat bestaat uit een product van functies

D (XY²) = y² + 2xy en '

-XY is een homologe manier

d (-xy) = -y -x en '

Ze worden in gelijkheid vervangen, wetende dat nul derivaat nul is.

3y³ + 9xy² en ' - 2 en' + en² + 2xy en ' - y - x en' = 0

De elementen die de term hebben en 'zijn gegroepeerd aan één kant van gelijkheid

Kan u van dienst zijn: Colineale vectoren

3y³ + En² - y = -9xy² en ' + 2 en' + x en '

De gemeenschappelijke factor en 'in het juiste lid van gelijkheid wordt geëxtraheerd

3y³ + En² - y = y '(-9xy² + x + 2)

Ten slotte vermenigvuldigt de term en '. Dus het verkrijgen van de expressie die overeenkomt met de impliciete derivaat van Y met betrekking tot x.

en '= dy/dx = (3y³ + En² - y)/(-9xy² + x + 2)

Kettingregel

In de impliciete afleiding wordt de kettingregel altijd gerespecteerd. Alle differentiële uitdrukkingen worden gegeven afhankelijk van de onafhankelijke variabele x. Zodat elke variabele θ die verschilt van X de term dθ/dx moet bevatten nadat hij is afgeleid.

Deze term verschijnt alleen in de eerste graad of met exponent gelijk aan 1. Deze kwaliteit maakt het volledig duidelijk onder traditionele factorisatiemethoden. Zodat het mogelijk wordt om de uitdrukking te verkrijgen die het differentiaal dθ/dx definieert.

In de kettingregel wordt de progressieve aard van het differentiatie- of derivaatproces getoond. Waarbij voor elke samengestelde functie f [g (x)] de differentiële expressie van f moet zijn

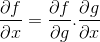
Operationele volgorde

In elke toegepaste formule- of afleidingwetgeving moet rekening worden gehouden met de volgorde van de variabelen. De criteria die verband houden met de onafhankelijke variabele worden gerespecteerd, zonder de correlatie ervan met de afhankelijke variabele te wijzigen.

De verhouding van de afhankelijke variabele op het moment van afgeleid wordt direct genomen.; Met uitzondering dat dit zal worden beschouwd als een tweede functie, zijn daarom de ketenregelcriteria voor gemengde functies toegepast.

Dit kan worden ontwikkeld in uitdrukkingen met meer dan 2 variabelen. Onder dezelfde principes zullen alle differentiëlen die verwijzen naar afhankelijke variabelen worden aangegeven.

Kan u van dienst zijn: wat is de richtlijn? (Geometrie)

Grafisch dezelfde criteria worden afgehandeld die het afgeleide definieert. Terwijl het derivaat de helling is van de lijn die op de curve in het vlak raakt, vertegenwoordigen de rest van de differentiëlen die behoren tot de afhankelijke variabelen (dy/dx, dz/dx) raakvlakken voor de vectorlichamen beschreven door de functies van meerdere variabele.

Impliciet van een functie

Er wordt gezegd dat een functie impliciet wordt gedefinieerd, als de uitdrukking y = f (x) kan worden weergegeven als een meervoudige variabele functie f (x, y) = 0 terwijl f is gedefinieerd in vlak r².

3xy³ - 2y + xy² = x en kan worden geschreven in de 3xy -vorm³ - 2y + xy² - Xy = 0

Gezien de onmogelijkheid om de functie Y = F (x) te verklaren.

Geschiedenis

De differentiële calculus begon te worden benoemd door verschillende wiskundige onderzoekers, rond de zeventiende eeuw. De eerste keer dat het werd genoemd, was via de bijdragen van Newton en Leibniz. Beide behandelden de differentiële calculus vanuit verschillende gezichtspunten, maar convergeren in hun resultaten.

Terwijl Newton zich concentreerde op differentiatie als een snelheid of variatie, was de Leibniz -benadering geometrischer. Men kan zeggen dat Newton de vermoedens heeft aangevallen die door Apollonius van Perge en Leibniz de geometrische ideeën van Fermat hebben aangevallen en Leibniz.

De impliciete afleiding verschijnt onmiddellijk wanneer de differentiële en uitgebreide vergelijkingen overwegen. Ze breidden het geometrische concept van Leibniz uit tot R³ en zelfs multidimensionale ruimtes.

Toepassingen

Impliciete derivaten worden in verschillende situaties gebruikt. Ze zijn gebruikelijk in wisselkoersproblemen tussen gerelateerde variabelen, waar, afhankelijk van het onderzoeksgevoel, de variabelen worden beschouwd als afhankelijk of onafhankelijk.

Ze hebben ook interessante geometrische toepassingen, zoals in problemen van reflecties of schaduwen, op cijfers waarvan de vorm wiskundig kan worden gemodelleerd.

Kan u van dienst zijn: quota -bemonstering: methode, voor-, nadelen, voorbeelden

Ze zijn van frequent gebruik op het gebied van economie en engineering, evenals in verschillende onderzoeken naar natuurlijke fenomenen en experimentele gebouwen.

Opgeloste oefeningen

Oefening 1

Definieer de impliciete expressie die DY/DX definieert

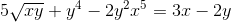
Elk element is anders dan de uitdrukking

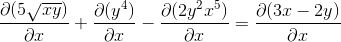
Het vaststellen van de kettingregel in elke competente zaak

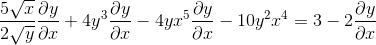
Groepering aan één kant van gelijkheid de elementen met dy/dx

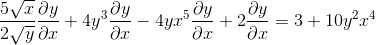
Is factureren met behulp van de gemeenschappelijke factor

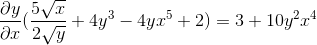
Wordt gewist door het verkrijgen van de gezochte uitdrukking

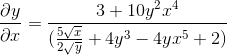
Oefening 2

Definieer de impliciete expressie die DY/DX definieert

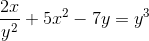
De derivaten uiten om uit te voeren

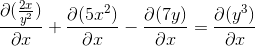
Impliciet afkomstig volgens de ketenregel

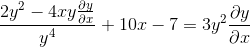
Behandeling van gemeenschappelijke elementen

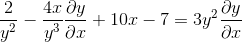
Groepering van de term dy/dx aan één kant van gelijkheid

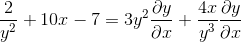
Gemeenschappelijke factor voor differentiaal element

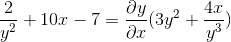
We wissen en verkrijgen de gezochte uitdrukking

Referenties

1. Calculus van een enkele variabele. Ron Larson, Bruce H. Edwards. Cengage Learning, 10 november. 2008
2. De impliciete functie -stelling: geschiedenis, theorie en toepassingen. Steven G. Krantz, Harold R. Parken. Springer Science & Business Media, 9 november. 2012
3. Multivariabele analyse. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 december. 2010
4. Systeemdynamiek: modellering, simulatie en controle van mechatronische systemen. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 maart. 2012
5. Calculus: wiskunde en modellering. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 januari. 199999