Quasiviteit formule en vergelijkingen, voorbeelden, oefening

De Quasieve beoordeling, quasi -variantie of ongezonde variantie is een statistische maat voor de dispersie van de gegevens van een steekproef Wat betreft het gemiddelde. De steekproef bestaat op zijn beurt uit een reeks gegevens uit een groot universum, genaamd bevolking.

Het wordt op verschillende manieren aangeduid, hier is het gekozen S_C² En om het te berekenen, volgt de volgende formule:

Figuur 1. De definitie van quasiviteit. Bron: f. Zapata.

Waar:

-S_C ² = De quasiriance of variantie van de steekproef (steekproefvariantie)

-X_Je = Elk van de voorbeeldgegevens

-N = Aantal observaties

-X = Het gemiddelde van het monster

Aangezien de eenheid van de monster quasiviteit het kwadraat is van de eenheid waarin het monster komt, heeft het bij het interpreteren van de resultaten de voorkeur om met de te werken met de quasi standaardafwijking of standaardafwijking van het monster.

Dit wordt aangeduid als S_C En het wordt verkregen door de vierkantswortel van de quasivariantie te extraheren:

S_C = √ s_C ²

De quasiriance is vergelijkbaar met de variantie S², met het enige verschil dat in de noemer daarvan is N-1, Terwijl het in de variantie alleen wordt verdeeld door N. Het is duidelijk dat wanneer n erg groot is, de waarden van beide meestal hetzelfde zijn.

Wanneer de waarde van de quasiriance bekend is, kunt u die van de variantie onmiddellijk weten.

[TOC]

Voorbeelden van quasiviteit

U wilt de kenmerken van elke populatie weten: mensen, dieren, planten en in het algemeen elk type objecten. Maar het analyseren van de hele populatie is misschien geen gemakkelijke taak, vooral als het aantal elementen erg groot is.

Vervolgens worden er monsters genomen, in de hoop dat hun gedrag dat van de bevolking weerspiegelt en er dus in staat is conclusies te trekken, dankzij welke middelen zijn geoptimaliseerd. Dit staat bekend als Statistische gevolgtrekking.

Hier zijn enkele voorbeelden waarin de quasiriance en de quasi -geassocieerde standaardafwijking dienen als een statistische indicator door erop te wijzen dat de verkregen resultaten met betrekking tot het gemiddelde.

Het kan u van dienst zijn: Perimeter van de cirkel: hoe u het eruit haalt en formules, opgeloste oefeningen

1.- De marketingdirecteur van een bedrijf dat autobatterijen produceert, moet in maanden de gemiddelde batterijduur schatten.

Selecteer hiervoor willekeurig een voorbeeld van 100 batterijen van dat gekochte merk. Het bedrijf behoudt een record van kopersgegevens en kan ze interviewen om de duur van de batterijen te kennen.

Figuur 2. Cuasive Appraise is nuttig voor het maken van conclusies en kwaliteitscontrole. Bron: Pixabay.

2.- Het academische management van een universitaire instelling moet de registratie van het volgende jaar schatten, het aantal studenten analyseren dat naar verwachting de onderwerpen goedkeuren.

Van elk van de secties die momenteel het fysieke onderwerp I bestuderen, kan het adres bijvoorbeeld een steekproef van studenten selecteren en de prestaties in genoemde voorzitter analyseren. Op deze manier kunt u afleiden hoeveel studenten natuurkunde II in de komende periode zullen studeren.

3.- Een groep astronomen richt hun aandacht op een deel van de lucht, waar een bepaald aantal sterren met bepaalde kenmerken wordt waargenomen: grootte, massa en temperatuur bijvoorbeeld.

Het is de moeite waard om te vragen of de sterren in een andere vergelijkbare regio dezelfde kenmerken zullen hebben, waaronder sterren in andere sterrenstelsels, zoals de aangrenzende wolken van Magallanes of Andromeda.

Waarom verdelen tussen N-1?

In de quasiriance is het verdeeld tussen N-1 in plaats van N En het is omdat de quasiriance een is Stond op schatter, Zoals in het begin vermeld.

Het gebeurt dat het uit dezelfde populatie mogelijk is om veel monsters te extraheren. De variantie van elk van deze monsters kan ook worden gemiddeld, maar het gemiddelde van deze varianties blijkt niet gelijk te zijn aan de variantie van de populatie.

Kan u van dienst zijn: relatieve waarde

In feite heeft het gemiddelde van de varianties van de steekproef de neiging om de variantie van de populatie te onderschatten, tenzij deze wordt gebruikt N-1 In de noemer. Het kan worden geverifieerd dat de verwachte waarde van de quasiviteit e (s_C²) is precies s².

Daarom wordt gezegd dat de quasiriance ontstaat en een betere schatter is van de populatievariantie s².

Alternatieve manier om de quasieve beoordeling te berekenen

Er wordt gemakkelijk aangetoond dat quasiriance ook als volgt kan worden berekend:

S_C² = [∑x² / (N -1)] - [∑NX² / (N-1)]

De standaardscore

Door de afwijking van het monster te hebben, kunnen we weten hoeveel standaardafwijkingen een bepaalde waarde X hebben, hetzij boven of onder het gemiddelde.

Hiervoor wordt de volgende dimensieloze uitdrukking gebruikt:

Standaardscore = (x - x) / s_C

Oefening opgelost

Bereken de quasiriance en de quasi -typische afwijking van de volgende gegevens, die bestaan ​​uit maandelijkse betalingen in $ gedaan door een verzekeringsmaatschappij aan een particuliere kliniek.

863 903 957 1041 1138 1204 1354 1624 1698 1745 1802 1883

a) Gebruik de definitie van quasiviteit die in het begin wordt gegeven en verifieer ook het resultaat door de alternatieve vorm die in de voorgaande sectie wordt gegeven.

b) Bereken de standaardscore van de tweede gegevens, lees van boven naar beneden van boven naar beneden.

Oplossing voor

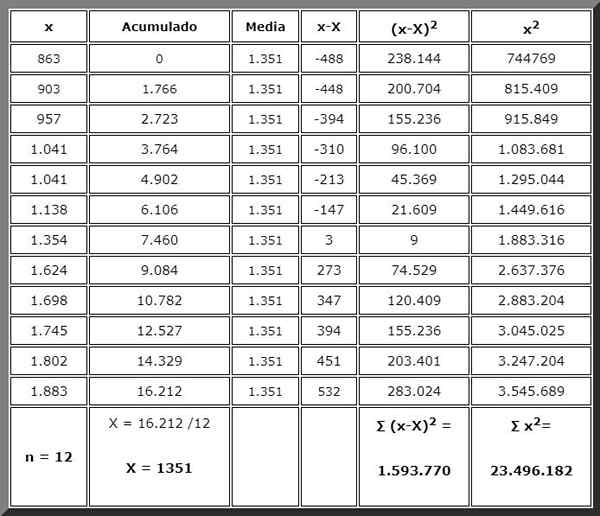
Het probleem kan met de hand worden opgelost met behulp van een eenvoudige of wetenschappelijke calculator, waarvoor we op volgorde moeten doorgaan. En hiervoor niets beter dan het organiseren van de gegevens in een tabel zoals hieronder getoond:

Dankzij de tabel heeft u informatie georganiseerd en de bedragen die nodig zijn in de formules bevinden zich aan het einde van de respectieve kolommen, klaar om onmiddellijk te gebruiken. Summaties worden vetgedrukt aangegeven.

Kan u van dienst zijn: wat zijn de 7 elementen van de omtrek?

De gemiddelde kolom wordt altijd herhaald, maar het is de moeite waard omdat het handig is om de waarde in beeld te hebben, om elke rij van de tabel te vullen.

Ten slotte wordt de vergelijking voor de in het begin gegeven quasiriance toegepast, alleen de waarden worden vervangen en in termen van de som hebben we deze al berekend:

S_C² = 1.593.770 / (12-1) = 1.593.770/11 = 144.888.2

Dit is de waarde van de quasiriance en zijn eenheden zijn "dollars in het kwadraat", wat niet veel praktisch zinvol is, dus de standaardquasiden van het monster worden berekend, wat niets meer is dan de vierkantswortel van de quasivariantie:

S_C = ((√144.888.2) $ = 380,64 $

Het wordt onmiddellijk bevestigd dat deze waarde ook wordt verkregen met de alternatieve vorm van de quasivariantie. De benodigde som bevindt zich aan het einde van de laatste kolom aan de linkerkant:

S_C² = [∑x² / (N-) - [∑NX² / (N-1)] = [23.496.182/11] - [12 x 1351²/ elf]

= 2.136.016.55 - 1.991.128,36 = 144.$ 888 kwadraat

Het is dezelfde waarde verkregen met de formule die aan het begin wordt gegeven.

Oplossing B

De tweede waarde van boven naar beneden is 903, de standaardscore is

Standaardscore van 903 = (x - x) / s_C = (903 - 1351)/380.64 = -1.177

Referenties

1. Canavos, G. 1988. Waarschijnlijkheid en statistieken: toepassingen en methoden. McGraw Hill.
2. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
3. Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.
4. Dispersiemaatregelen. Hersteld van: thales.CICA.is.
5. Walpole, r. 2007. Waarschijnlijkheid en statistieken voor engineering en wetenschap. Pearson.