Tukey -test in wat is, meester, oefening opgelost

De Tukey -test Het is een methode die tot doel heeft individuele gemiddelden te vergelijken van een variantieanalyse van verschillende monsters onder.

De test, gepresenteerd in 1949 door John.W. Tukey, maakt het mogelijk om te onderscheiden of de verkregen resultaten aanzienlijk verschillen of niet. Het staat ook bekend als de Tukey eerlijk gezegd significante verschiltest ((Tukey's HSD -test voor zijn acroniem in het Engels).

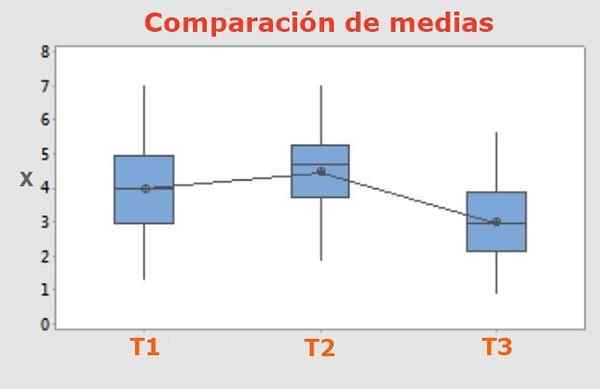
Figuur 1. De Tukey -test maakt het mogelijk om te onderscheiden of de verschillen in resultaat tussen drie of meer verschillende behandelingen die worden toegepast op drie of meer groepen gelijke kenmerken, significante en eerlijk verschillende gemiddelde waarden hebben.

In experimenten waarbij het wordt vergeleken tussen drie of meer verschillende behandelingen die op hetzelfde aantal monsters worden toegepast, is het noodzakelijk om te onderscheiden of de resultaten aanzienlijk verschillen of niet.

Er wordt gezegd dat een experiment in evenwicht is wanneer de grootte van alle statistische monsters in elke behandeling hetzelfde is. Wanneer de bemonsteringsgrootte voor elke behandeling anders is, is er dan een niet -balanced experiment.

Soms is het niet voldoende met een variantieanalyse (ANOVA) om te weten of in de vergelijking van verschillende behandelingen (of experimenten) toegepast op verschillende monsters ze de nulhypothese vervullen (ho: "Alle behandelingen zijn hetzelfde") of integendeel het Voortkomen op de alternatieve hypothese (ha: "ten minste een van de behandelingen is anders").

De Tukey -test is niet uniek, er zijn nog veel meer bewijs om monsters te vergelijken, maar dit is een van de bekendste en toegepaste.

[TOC]

Vergelijker en tukey -tabel

In de toepassing van deze test wordt een waarde berekend W genaamd de Tukey -comparator wiens definitie als volgt is:

W = q √ (mse /r)

Waar de factor Q Het wordt verkregen uit een tabel (tukey -tabel), die bestaat uit waardenrangen Q Voor verschillende behandelingen of experimenten. De kolommen geven de factorwaarde aan Q Voor verschillende vrijheidsgraden. Normaal gesproken hebben de beschikbare tabellen relatieve middelen van 0.05 en 0.01.

Kan u van dienst zijn: in afwachting van een lijn: formule en vergelijkingen, representatie, voorbeelden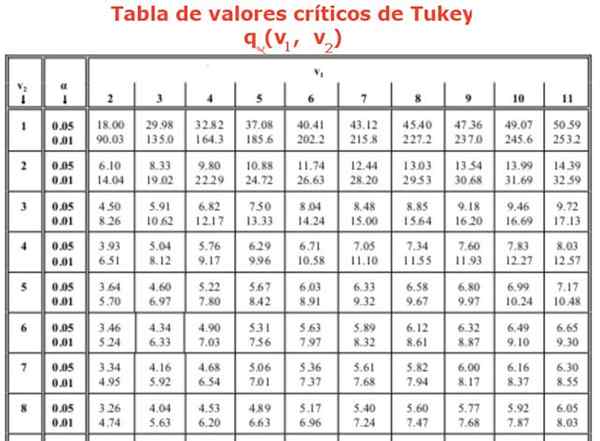

In deze formule verschijnt binnen de vierkantswortel de MSE -factor (gemiddeld vierkant van de fout) gedeeld door R, wat het aantal herhalingen aangeeft. De MSE is een getal dat normaal wordt verkregen uit een analyse van varianties (ANOVA).

Wanneer het verschil tussen twee gemiddelde waarden de waarde overschrijdt W (Tukey Comparator), dan wordt geconcludeerd dat dit verschillende gemiddelden zijn, maar als het verschil minder is dan het tukey -nummer, dan zijn het twee monsters met een statistisch identieke gemiddelde waarde.

Het W -nummer staat ook bekend als HSD -nummer (eerlijk gezegd significant verschil).

Dit alleen vergelijkingsnummer kan worden toegepast als het aantal toegepaste monsters voor de test van elke behandeling in elk van hen hetzelfde is.

Onevenwichtige experimenten

Wanneer om een ​​of andere reden de grootte van de monsters in elke behandeling anders is om te vergelijken, verschilt de hierboven beschreven procedure enigszins en staat bekend als bekend als Tukey-Kramer-test.

Nu wordt een nummer verkregen W Vergelijker voor elk paar behandelingen ik, j:

w (i, j) = q √ (½ mse /(ri +rj))

In deze formule is de factor die wordt verkregen uit de tukey -tabel. Genoemde factor die afhangt van het aantal behandelingen en de foutenvrijheidsgraden. R_Je Het is het aantal herhalingen in behandeling I, terwijl r_J Het is het aantal herhalingen in de J -behandeling.

Voorbeeldcase

Een konijnenfokker wil een betrouwbaar statistisch onderzoek maken dat aangeeft dat hij weet welke van de vier konijnenmesten voedselmerken het meest effectief is. Voor de studie vormt het vier groepen met zes en een halve konijnen die tot die tijd dezelfde voedingsomstandigheden hadden.

Van het experiment tot de eerste groep wordt het A1 genoemd omdat het zich zal voeden met het voedsel van merk 1, op dezelfde manier met groep A2, A3 en A4. Er wordt een tabel gemaakt waar de gewichtstoename (in ponden) van elk monster na een maand voedsel met de verschillende voedselmerken wordt geregistreerd, waardoor de volgende resultaten worden verkregen: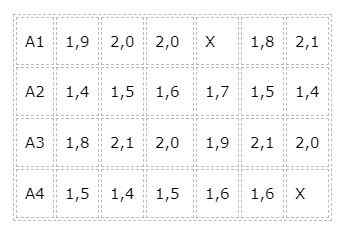Hoewel het begon met een uitgebalanceerd experiment, in de zin dat het aantal konijnen waarop de behandeling zou worden toegepast hetzelfde was, kon het experiment niet op deze manier worden voltooid.

Kan u van dienst zijn: negatieve homotecia

De redenen waren dat in groepen A1 en A4 sterfgevallen plaatsvonden vanwege oorzaken die niet te wijten waren aan voedsel, omdat een van de konijnen door een insect werd gehakt en in het andere geval de dood zeker de oorzaak was van een aangeboren defect. Zodat de groepen onevenwichtig zijn en het dan nodig is om de Tukey-Kramer-test toe te passen.

Oefening opgelost

Om de berekeningen niet te veel uit te breiden, zal een geval van een evenwichtig experiment worden genomen als een oefening opgelost. Het volgende wordt als gegevens beschouwd:

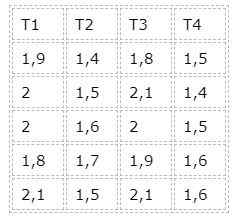
In dit geval zijn er vier groepen die overeenkomen met vier verschillende behandelingen. We zien echter dat alle groepen hetzelfde aantal gegevens hebben, dus het is dan een evenwichtig geval.

Om de ANOVA -analyse uit te voeren, de tool die is opgenomen in de spreadsheet van LibreOffice. Andere spreadsheets zoals Uitblinken Ze hebben deze tool voor gegevensanalyse opgenomen. Hieronder is een samenvattende tabel die heeft gevolgd na de variantieanalyse (ANOVA):

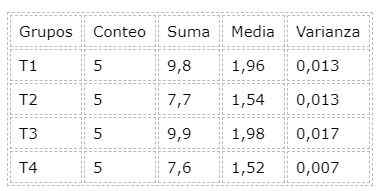
Uit variantieanalyse is er ook de waarde P, die bijvoorbeeld 2,24E-6 ver onder 0 is.05 van het significantieniveau, wat direct leidt tot het afwijzen van de nulhypothese: alle behandelingen zijn gelijk. 

Dat wil zeggen, onder de behandelingen hebben sommige verschillende gemiddelde waarden, maar je moet weten wat de significante en eerlijk gezegd anders (HSD) zijn vanuit het statistische oogpunt met behulp van Tukey -test.

Om het nummer W te vinden of als het HSD -nummer ook bekend is, hebben we het gemiddelde kwadraat van de MSE -fout nodig. Uit ANOVA -analyse wordt verkregen dat de som van vierkanten binnen de groepen SS = 0,2 is; En het aantal vrijheidsgraden binnen de groepen is DF = 16 met deze gegevens kunnen we mse vinden:

Kan u van dienst zijn: papomudas

MSE = SS/DF = 0,2/16 = 0,0125

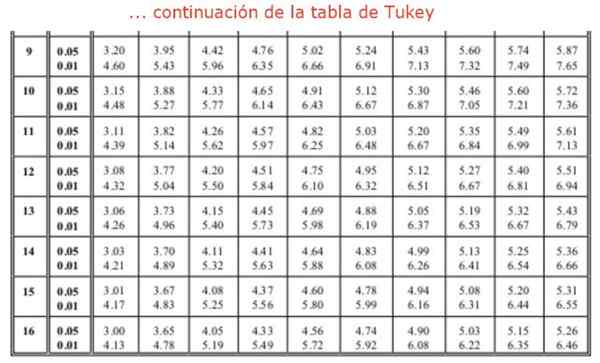
Het is ook nodig om de factor te vinden Q van tukey, met behulp van de tabel. Het wordt gezocht in kolom 4 die overeenkomt met de 4 groepen of behandelingen om te vergelijken en rij 16, omdat de ANOVA -analyse 16 vrijheidsgraden binnen de groepen liet zien. Dit leidt ons naar een waarde van Q gelijk aan: Q = 4.33 overeenkomend met 0,05 significantie of 95% betrouwbaarheid. Ten slotte wordt de waarde voor het "eerlijk significant verschil" gevonden:

W = HSD = Q √ (mse /r) = 4,33 √ (0.0125 /5) = 0.2165

Om te weten wat de eerlijk verschillende groepen of behandelingen zijn, moet u de gemiddelden van elke behandeling weten:

Het is ook noodzakelijk om de verschillen te kennen tussen de gemiddelde waarden van paren behandelingen, die in de volgende tabel worden weergegeven:

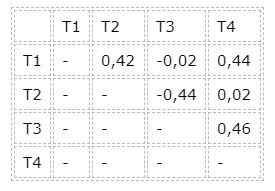T3- en T1 -groepen, evenals groepen T2 en T4, zijn van identieke resultaten. Dus de eerlijk verschillende groepen zijn groepen T1 en T2 of T3 en T4, omdat het verschil in hun gemiddelde waarden de HSM -waarde van de Tukey -test overschrijdt.

Er wordt geconcludeerd dat de beste behandelingen, in termen van het maximaliseren van het resultaat, de T1 of de T3 zijn, die onverschillig zijn vanuit het statistische standpunt. Om te kiezen tussen T1 en T3, moeten andere factoren buiten de hier gepresenteerde analyse worden gezocht. Bijvoorbeeld prijs, beschikbaarheid, etc.

Referenties

1. Cochran William en Cox Gertrude. 1974. Experimentele ontwerpen. Trilla's. Mexico. Derde herdruk. 661p.
2. Snedecor, g.W. En Cochran, W.G. 1980. Statistische methoden. Zevende ed. Iowa, de Iowa State University Press. 507P.
3. Staal, r.G.D. En Torrie, J.H. 1980. Principes en procedures van statistieken: een biometrische benadering (2e ed.)). McGraw-Hill, New York. 629P.
4. Tukey, J. W. 1949. Individuele vergelijking middelen in de variantieanalyse. Biometrie, 5: 99-114.
5. Wikipedia. Tukey's test. Opgehaald uit: in.Wikipedia.com