Radiale belasting Hoe wordt berekende, opgeloste oefeningen

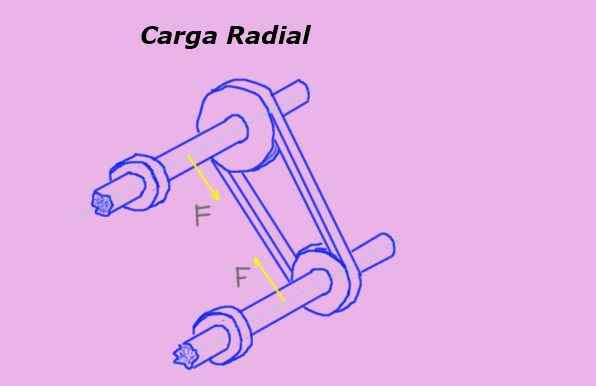
De Radiale belasting Het is de kracht die loodrecht op de symmetrieas van een object wordt uitgeoefend en wiens werklijn door deze as gaat. Een riem op een poelie legt bijvoorbeeld een radiale belasting op aan het lager of lager van de as van hetzelfde.

In figuur 1 vertegenwoordigen de gele pijlen radiale krachten op de assen vanwege de spanning van de riem die door de katrollen gaat.

Figuur 1. Radiale belasting op poeliesassen. Bron: zelf gemaakt.

De maateenheid van de radiale belasting in het internationale systeem of als het de Newton (n) is. Maar andere krachtenheden worden ook gebruikt om het te meten, zoals de kilogram-force (kg-f) en de pondsterkte (lb-f).

[TOC]

Hoe wordt het berekend? 

Om de waarde van de radiale belasting in de elementen van een structuur te berekenen, moeten de volgende stappen worden gevolgd:

- Maak het krachtenschema op elk element.

- Pas de vergelijkingen toe die het translationele saldo garanderen; dat wil zeggen, de som van alle krachten is nietig.

- Overweeg de vergelijking van knooppunten of momenten zodat de rotatiebalans is vervuld. In dit geval moet de som van alle knooppunten nietig zijn.

- Bereken de krachten om de radiale belastingen te identificeren die in elk van de elementen werken.

Opgeloste oefeningen

-Oefening 1

De volgende figuur toont een poelie waardoor een gespannen poelie doorgaat met spanning T. De poelie is gemonteerd op een as die op twee chumaceras rust. Het midden van een van hen is op afstand L₁ Van het midden van de poelie. Aan de andere kant is de andere chumacera, op afstand l₂.

Kan u van dienst zijn: Higroscopiciteit: concept, hygroscopische stoffen, voorbeelden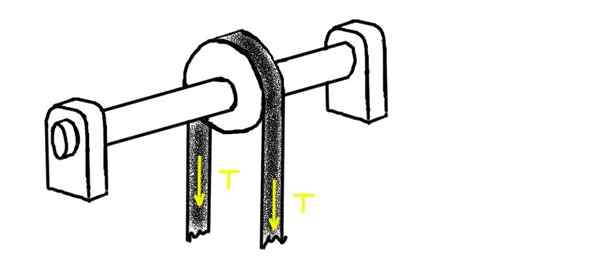Figuur 2. Poelie waardoor een gespannen riem voorbijgaat. Bron: zelf gemaakt.

Bepaal de radiale belasting op elk van de chumaceras, ervan uitgaande dat het gewicht van de as en de poelie vrij lager zijn dan de uitgeoefende spanning.

Neem als waarde voor de 100 kg-F-riemspanning en voor afstanden l₁= 1 m en l₂= 2 m.

Oplossing

In de eerste plaats wordt een diagram van de krachten die op de as werken, gemaakt.

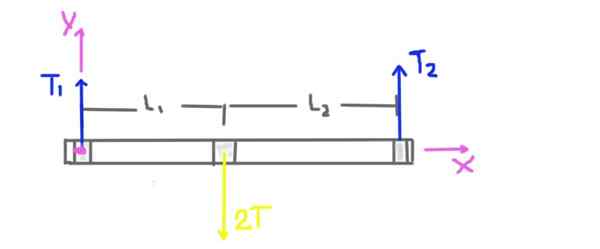figuur 3. Oefeningskrachten Diagram 1.

De katrolspanning is t, maar de radiale belasting op de as in de positie van de poelie is 2t. Het gewicht van de as en de poelie wordt niet in aanmerking genomen omdat de probleemverklaring ons vertelt dat deze veel lager is dan de spanning die op de riem wordt toegepast.

De radiale reactie van de ondersteuningssteunen wordt veroorzaakt door de radiale krachten of belastingen T1 en T2. De afstanden L1 en L2 van de steunen naar het midden van de poelie worden ook aangegeven in het diagram.

Het coördinatensysteem wordt ook getoond. Het koppel of het totale moment op de as zal worden berekend als een centrum de oorsprong van het coördinatensysteem en zal positief zijn in de Z -richting.

Evenwichtsvoorwaarden

De evenwichtsvoorwaarden zijn nu vastgesteld: som van dezelfde nul en som van Torques gelijk aan nul.

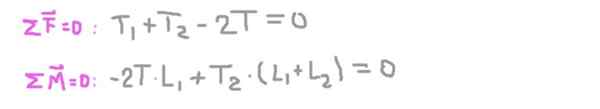
Uit de tweede vergelijking de radiale reactie op de as op ondersteuning 2 (t₂), vervangen in de eerste en het opruimen van de radiale reactie op de as in steun 1 (t₁)).

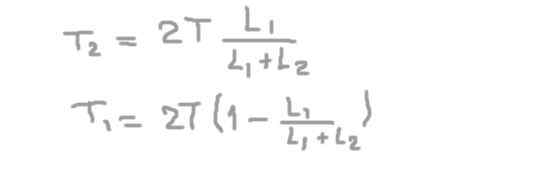Als we de numerieke gegevens vervangen, verkrijgen we dat de radiale belasting of kracht op de as in de positie van ondersteuning 1 is:

T₁= (2/3) t = 66,6 kg-f

Het kan u van dienst zijn: Kalibratiecurve: waar is het voor, hoe het te doen, voorbeelden

En de radiale belasting op de as in de ondersteuning van ondersteuning 2 is:

T₂= (4/3) t = 133,3 kg-f.

Oefening 2

De volgende figuur toont een systeem dat bestaat uit drie katrollen A, B, C All the Radio R. De katrollen zijn verbonden door een riem met een T -spanning.

Assen A, B, C doorgeeft gesmeerde lagers. De scheiding tussen de centra van assen A en B is 4 keer de straal R. Evenzo is de scheiding tussen assen B en C ook 4R.

Bepaal de radiale belasting op de assen van de katrollen A en B, ervan uitgaande dat de spanning van de riem 600n is.

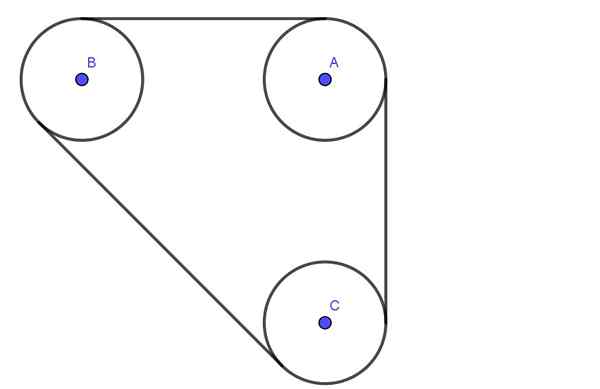Figuur 4. Poeliesysteem. Oefening 2. (Eigen uitwerking)

Oplossing

Het begint met het tekenen van een diagram van de krachten die op poelie a en b werken. Op de eerste heb je beide tsions₁ en t₂, evenals de kracht f_NAAR Dat het lager uitoefent op de as van de poelie.

Evenzo heb je op poelie B spanningen t₃ , T₄ en de kracht f_B dat het lager op de as van hetzelfde uitoefent. De radiale belasting op de as van poelie A is de kracht f_NAAR en de radiale belasting op de B is de kracht f_B.

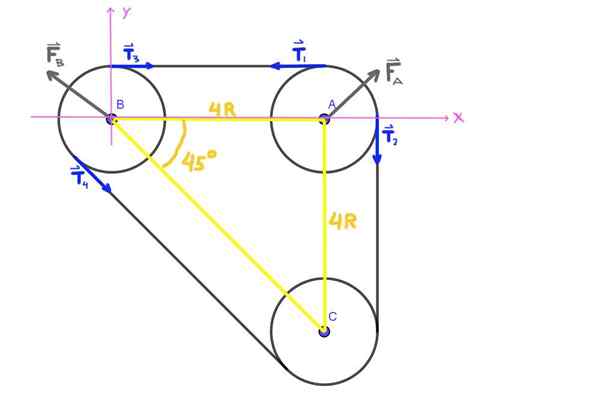Figuur 5. Forces Diagram, Oefening 2. (Eigen uitwerking)

As assen A, B, C vormen een isorectangle -driehoek, de ABC -hoek is 45 °.

Alle spanningen t₁ , T₂ , T₃ , T₄ In de figuur worden dezelfde module t getoond, wat de riemspanning is.

Balansconditie voor katrol a

Nu schrijven we de balansvoorwaarde voor de poelie waaraan deze niets anders is dan de som van alle kracht die op de poelie handelt, moet ongeldig zijn.

Het scheiden van de componenten x en y van de krachten en het toevoegen van (vectoriaal) het volgende paar scalaire vergelijkingen wordt verkregen:

Kan u van dienst zijn: Titan (satelliet)

F_NAARX - T = 0; F_NAAREN - T = 0

Deze vergelijkingen leiden tot de volgende gelijkheid: F_Bijl = F_OH = T.

Daarom heeft de radiale belasting grootte gegeven door:

F_NAAR = (T² + t²)^1/2 = 2^1/2∙ t = 1,41 ∙ t = 848,5 n. Richting van 45 °. 

Balansconditie voor poelie B

Evenzo schrijven we de evenwichtsconditie voor poelie B. Voor component X heb je: F_BX + T + t ∙ cos45 ° = 0

En voor de component y: f_BEN + T ∙ Sen45 ° = 0

Dus:

F_Bx = - t (1+2^-1/2) en f_Door = -T ∙ 2^-1/2

Dat wil zeggen, de grootte van de radiale belasting op poelie B is:

F_B = ((1+2^-1/2) ² + 2^-1))^1/2∙ t = 1,85 ∙ t = 1108,66 n en het adres is 135 °.

Referenties

1. Beer F, Johnston E, DeWolf J, Mazurek, D. Materiaalmechanica. Vijfde editie. 2010. MC Graw Hill. 1-130.
2. Gere J, Goodno, B. Materiaalmechanica. Achtste editie. Cengage leren. 4-220.
3. Giancoli, D. 2006. Fysica: principes met toepassingen. 6^TTH ED. Prentice Hall. 238-242.
4. Hibbeler R. Materiaalmechanica. Achtste editie. Prentice Hall. 2011. 3-60.
5. Valera Negrete, J. 2005. ALGEMENE FYSICA -NOTIES. UNAM. 87-98.