Capaciteitseenheden, formules, berekening, voorbeelden

De Capaciteit Het is de relatie tussen de belasting van een condensator of trainer, gemeten in Coulomb, en zijn elektrische potentiaal of spanning, gemeten in volt. Het wordt uitgedrukt in Faradio (F) -eenheden, ter ere van Michael Faraday (1791-1867).

Capaciteit wordt ook gedefinieerd als de eigenschap of capaciteit van een condensor of set elektrische condensatoren, die wordt gemeten door de hoeveelheid elektrische lading die afzonderlijk kan worden opgeslagen, per eenheid van verandering van de elektrische potentiaal.

De lampen, evenals elk ander elektrisch apparaat, moeten deel uitmaken van hun werking om te capaciteiten. Bron: Pixabay.

De term capaciteit wordt geïntroduceerd als gevolg van het creëren van een elektrisch apparaat genaamd de condensator, uitgevonden door Pruisische wetenschapper Ewald Georg von Kleist, in 1745, en ongeacht de Nederlandse natuurkundige Pieter van Musschenbroek.

Condensatoren zijn elektrische apparaten die elektrische lading opslaan en deze onmiddellijk downloaden. Deze eigenschap is gebruikt in tal van elektrische apparaten, zoals televisie, radio, lampen, computer, onder vele anderen in het dagelijks leven.

[TOC]

Condensator en capaciteit

Een condensator of condensator bestaat uit twee bestuurders die gelijke ladingen hebben en anderszins. Bestuurders worden pantserpantser of condensorplaten genoemd.

Een plaque is gekoppeld aan de positieve (+) terminal van de ene batterij, terwijl de andere plaat is gekoppeld aan het negatieve (-). Aangezien de platen gelijke belastingen hebben en het tegenovergestelde teken, is de netto belasting van een condensator nul (0).

Capaciteit is de relatie tussen de belasting van een bestuurder of geleiders die een condensator vormen en de waarde van het spanningsverschil tussen de condensorplaten.

Kan u van dienst zijn: Rosario koelmiddel

Eenheden en formules

De capaciteitsformule is als volgt:

C = Q / V

Waar C capaciteit is, Q de belasting (waarvan de eenheid de Coulomb is) en v  De spanning (volt)

De capaciteitseenheid is de Faradio (F), die gelijkwaardig is aan Coulomb / Voltio. De Faradio is een zeer grote eenheid, dus microfradium (µF) wordt gebruikt, gelijk aan 10^-6 farad; of de Faradio Peak (PF), die gelijkwaardig is aan 10^-12 farad.

Hoe wordt de capaciteit berekend?

Wat zal de capaciteitswaarde zijn van een condensator waarvan de platen een belasting van 5 · 10 hebben^-3 Coulomb en een 6 volt spanningsverschil?

De formule toepassen die we oplossen:

C = Q / V

= (5 · 10^-3 Coulomb) / (6 volt)

= 8.33 · 10^-4  farad

Voorbeelden

De capaciteitsformule varieert afhankelijk van het type condensator.

Parallelle platen condensator

C = Kε_ofAdvertentie

K is de diëlektrische constante, die een waarde heeft van 1 in de lucht en de leegte. Om deze reden is de formule gereduceerd tot:

C = ε_ofAdvertentie

ε_of Het is de diëlektrische constante, waarvan de waarde bijna 8.854 · 10 is^-12 F · m^-1, A is het gebied of oppervlak van de parallelle platen uitgedrukt in M², terwijl D De afstand die de parallelle platen scheidt.

Bolvormig condensator

C = 4πε_ofR

Waarbij r de straal van de bol in meters is.

Concentrische bollen

C = 4πε_of / (1/ r₁ - 1/r₂))

Concentrische cilindercondensator

C = 2πε_ofl/ln (r₂ / R₁))

Waar l is de lengte van concentrische cilinders in meters.

Opgeloste oefeningen

Parallelle platte platen condensator

Wat zal de capaciteit zijn van een condensator of condensator in de lucht met een oppervlakte van zijn 3 cm platen² en gescheiden door een afstand van 2 mm?

Kan u van dienst zijn: 12 voorbeelden van chemische bases

We hebben de formule:

C = ε_ofAdvertentie

En de gegevens:

ε_of = 8.854 x 10^-12 F · m^-1

A = 3 cm² (3 · 10^-4 M²))

D = 2 mm (2 · 10^-3 M)

Ga verder met vervanging:

C = (8.854 · 10^-12 F · m^-1) (3 · 10^-4 M²) / (2 · 10^-3 M)

= 1,3281 · 10^-14 F

Condensator of bolvormige condensator

Als de aarde wordt beschouwd als een sferische condensator met een straal (r) van 6.370 km: wat zal de waarde van uw capaciteit zijn?

Gegevens:

C = 4πε_ofR

Π = 3.1416

ε_of = 8.854 · 10^-12 F.M^-1

R = 6.370 km (6.37 · 10⁶ M)

De waarden in de capaciteitsformule worden opnieuw vervangen:

C = (4 · 3.1416) (8.854 · 10^-12 F · m^-1) (6.37 · 10⁶ M)

= 7,09 · 10^-8 F

= 709 µF

Combinatie van condensatoren

Condensatoren of condensatoren kunnen in serie of parallel worden gecombineerd.

Serie -condensatoren

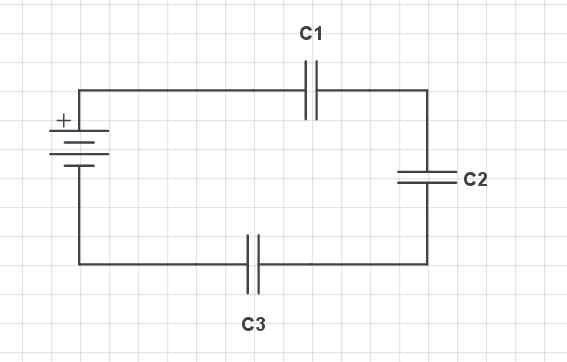Serie -condensatoren. Gabriel Bolívar -bron via Circuitbladen

De bovenste afbeelding toont drie series condensatoren (c₁, C₂ en C₃), evenals een batterij met zijn positieve (+) en negatieve (-) terminals. Deze condensatoren hebben een reeks kenmerken in relatie tot hun spanning, belasting en capaciteit.

Spanningsval (ΔV) in condensatoren

AV_T = AV₁   +   AV₂   +    AV₃

De totale spanningsval in een reeks seriële condensatoren is gelijk aan de som van de spanningsfalten van de condensatoren.

Last  van condensatoren

Q_T = Q₁ = Q₂ = Q₃

Dezelfde hoeveelheid belasting circuleert door de serie.

Condensatoren capaciteit

De equivalente capaciteit van seriële condensatoren heeft de volgende relatie:

1 c_eq  = 1/c₁  +   1 c₂   +   1 c₃

Parallelle condensatoren

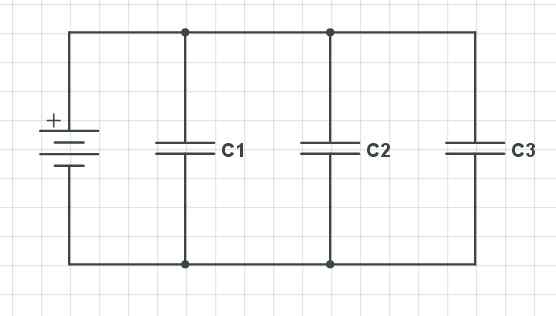Parallelle condensatoren. Gabriel Bolívar -bron via Circuitbladen.

We hebben drie condensatoren die parallel zijn gerangschikt (c₁, C₂ en C₃), die het volgende gedrag in verband met de spanningsval, belasting en capaciteit behouden:

Kan u van dienst zijn: alkenes

Spanningsdaling in condensatoren

AV_T  = AV₁  = AV₂  = AV₃

In parallelle condensatoren is de totale spanningsdaling in condensatoren dezelfde als de bestaande voor elk van de condensatoren.

Condensatoren

Q_T  = Q₁  +  Q₂  +  Q₃

In een systeem parallel is de totale belasting van de condensatoren gelijk aan de som van de belasting van alle condensatoren.

Condensatoren capaciteit

C_eq  = C₁  +  C₂   +  C₃

In een parallel systeem is de equivalente capaciteit daarvan gelijk aan de som van de capaciteiten van alle condensatoren.

Voorbeeld van een oefening

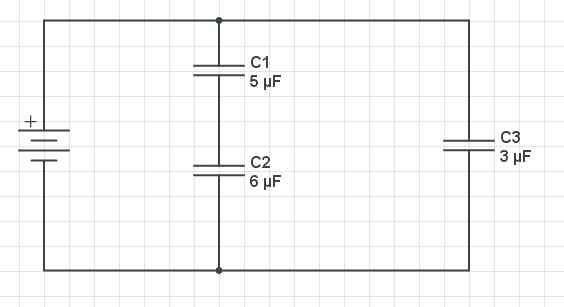Voorbeeld van een probleem en parallel condensatoren probleem. Gabriel Bolívar -bron via Circuitbladen.

Een schema van drie condensatoren wordt hierboven weergegeven: C₁ en C₂ Ze zijn in serie gerangschikt en ze zijn parallel met C₃. De condensatorencapaciteit zijn de volgende: C₁ = 5 µf, c₂ = 6 µF en C₃ = 3 µF. Vind de equivalente capaciteit van het circuit.

Ten eerste is de equivalente capaciteit van C₁ en C₂ die in serie zijn.

1 c_EQ1,2 = 1/c₁  +  1 c₂

1 c_EQ1,2 = 1/5 µF +1/6 µF

1 c_EQ1,2 = (11/30) µf

C_EQ1,2 = 30 µf / 11

= 2,72 µF

Condensatoren 1 en 2 zijn parallel met C₃. Dus de equivalente capaciteit van C₁, C₂ en C₃ is gelijk aan C_EQ1,2 +  C₃.

C_EQ1,2,3 = 2,72 µF +3 µF

= 5,72 µF

Referenties

1. Serway, r. NAAR. en Jewett, J. W. (2009). Natuurkunde voor wetenschap en engineering. Deel 2. Zevende editie. Redactioneel cengage leren.
2. Reddick, R en Halliday, D. (1965). Fysiek.  Deel 2. Tweede editie in het Spaans. Continentale redactionele s.NAAR.
3. Studie. (22 april 2015). Capaciteit: eenheden en formule. Hersteld van: studie.com
4. Lumes fysica. (S.F.)). Condensatoren in serie en parallel. Hersteld van: cursussen.Lumenarning.com
5. De redacteuren van Enyclopaedia Britannica. (2020). Capaciteit. Hersteld van: Britannica.com