Antiderivatieve formules en vergelijkingen, voorbeelden, oefeningen

A antiderivatief F (x) van een functie F(x) wordt ook primitief of gewoon de onbepaalde integrale van de genoemde functie genoemd, indien in een bepaald interval Je, Is het waar dat F '(x) = f (x)

Laten we bijvoorbeeld de volgende functie nemen:

f (x) = 4x³

Een antiderivatief voor deze functie is f (x) = x⁴, Omdat door F (x) af te leiden door de afleidingregel voor de bevoegdheden:

Het wordt precies verkregen f (x) = 4x³.

Dit is echter slechts een van de vele antiderivaten van F (X), omdat deze andere functie: G (X) = X⁴ + 2 Het is ook, omdat het door g (x) af te leiden met betrekking tot x, hetzelfde is verkregen terug f (x).

Laten we het controleren:

Onthoud dat degene die van een constante is afgeleid, is 0. Daarom naar de term x⁴ U kunt elke constante toevoegen en de afgeleide ervan blijft 4x³.

Er wordt geconcludeerd dat elke functie van de algemene vorm f (x) = x⁴ + C, waar C een echte constante is, dient als antiderivatief voor f (x).

Het vorige illustratieve voorbeeld kan als volgt worden uitgedrukt:

df (x) = 4x³ Dx

De niet -gedefinieerde antiderivatieve of integrale wordt uitgedrukt met het symbool ∫, daarom:

F (x) = ∫4x³ dx = x⁴ + C

Waarbij de functie f (x) = 4x³  Het heet integratie, en C is de Integratieconstante.

[TOC]

Voorbeelden van antiderivaten

Figuur 1. De anti -Hotley is niets meer dan een onbepaalde integraal. Bron: Pixabay.

Het vinden van een antiderivatief van een functie is eenvoudig in sommige gevallen waarin de derivaten bekend zijn. Wees bijvoorbeeld de functie f (x) = sen x, een niet -gecertificeerd voor het is een andere functie f (x), zodat het wordt verkregen als het wordt verkregen f (x).

Die functie kan zijn:

F (x) = - cos x

Laten we controleren of het waar is:

F '(x) = (- cos x)' =- (-sen x) = sin x

Daarom kunnen we schrijven:

∫sen x dx = -cos x + c

Naast het kennen van de derivaten, zijn er basis- en eenvoudige integratieregels om onbepaalde antiderivatief of integraal te vinden.

Kan u van dienst zijn: opeenvolgende derivaten

Wees een echte constante dan:

1.- ∫kdx = k ∫dx = kx + c

2.- ∫kf (x) dx = k ∫f (x) dx

Als een H (x) -functie kan worden uitgedrukt als de som of aftrekking van twee functies, dan is de onbepaalde integrale integratie ervan:

3.- ∫H (x) dx = ∫ [f (x) ± g (x)] dx = ∫f (x) dx ± ∫g (x) dx

Dit is eigendom van lineariteit.

De Machtsregel Voor integralen kan het op deze manier worden vastgesteld:

Deze regel heeft een duidelijke beperking: sinds de noemer N +1 Het kan niet worden gedaan 0, daarom n ≠ -1.

In het geval van n = -1 wordt de volgende regel gebruikt:

5.- ∫X ^-1 Dx = ln x +c

Het is gemakkelijk om aan te tonen dat de afgeleide van ln x het is precies X ^-1.

Differentiaalvergelijkingen

Een differentiaalvergelijking is er een waarin het onbekende is als een derivaat.

Nu, uit de vorige analyse, is het gemakkelijk om te beseffen dat de omgekeerde werking van het derivaat de ongedefinieerde antiderivatieve of integraal is.

Laat f (x) = y '(x), dat wil zeggen afgeleid van een bepaalde functie. We kunnen de volgende notatie gebruiken om deze afgeleide aan te geven:

Het volgt onmiddellijk dat:

dy = f (x) dx

Het onbekende van de differentiaalvergelijking is de functie y (x), degene wiens afgeleide f (x) is. Om het te wissen, is de vorige uitdrukking aan beide zijden geïntegreerd, wat gelijk is aan het toepassen van het antiderivatief:

∫dy = ∫f (x) dx

De linker integrale wordt opgelost door integratieregel 1, met k = 1 en dus wordt de gezochte -awaite gewist:

en (x) = ∫f (x) dx = f (x) + c

En omdat C een echte constante is, om te weten welke in elk geval geschikt is, moet de verklaring voldoende aanvullende informatie bevatten om de waarde van C te berekenen. Dit heet Begintoestand.

We zullen voorbeelden zien van de toepassing van dit alles in de volgende sectie.

Kan u van dienst zijn: punctuele schatting

Antiderivated oefeningen

- Oefening 1

Pas de integratieregels toe om de volgende niet -gedefinieerde antiderivaten of integralen van de gegeven functies te verkrijgen, waardoor de resultaten zoveel mogelijk worden vereenvoudigd. Het is handig om het resultaat te verifiëren door afleiding.

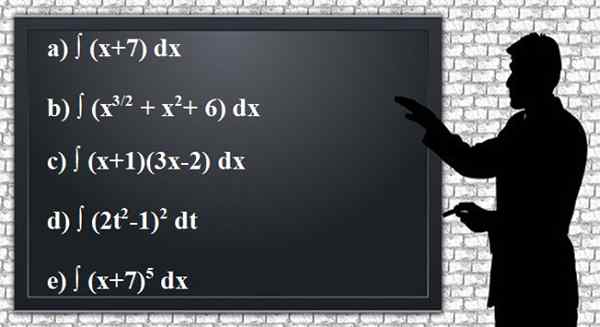Figuur 2. Gedefinieerde anteriveerde of integrale oefeningen. Bron: Pixabay.

Oplossing voor

We passen eerst regel 3 toe, omdat de integratie de som van twee voorwaarden is:

∫ (x +7) dx = ∫ xdx +∫7dx

Voor de eerste integraal wordt de regel van de bevoegdheden toegepast:

∫ xdx = (x² /2)+c₁

In de tweede integrale regel 1 is van toepassing, K = 7 zijn:

∫7dx = 7∫dx = 7x + c₂

En nu worden de resultaten toegevoegd. De twee constanten zijn gegroepeerd in één, generiek C:

∫ (x+7) dx = (x² /2) + 7x + c

Oplossing B

Door lineariteit ontbindt deze integrale ontbindingen in drie eenvoudigere integralen, waarop de regel van de bevoegdheden zal worden toegepast:

∫ (x^3/2 + X² + 6) dx = ∫xx^3/2 Dx + ∫x² dx +∫6 dx =

= (2/5) x^5/2 + (1/3) x³ + 6x + c

Merk op dat voor elke integraal een integratieconstante verschijnt, maar ze ontmoeten elkaar in een enkele oproep C.

Oplossing C

In dit geval is het handig om de distributieve eigenschap van de vermenigvuldiging toe te passen om de integratie te ontwikkelen. Vervolgens gebruikt u de regel van de bevoegdheden om elke integraal afzonderlijk te vinden, zoals in het voorgaande jaar.

∫ (x+1) (3x-2) dx = ∫ (3x²-2x+3x-2) dx = ∫ (3x² + X - 2) DX

De attente lezer zal zien dat de twee centrale termen vergelijkbaar zijn, daarom worden ze verminderd voordat ze worden geïntegreerd:

∫ (x+1) (3x-2) dx = ∫3x² dx + ∫ x dx + ∫- 2 dx = x³ + (1/2) x² - 2x + c

Oplossing e

Een manier om de integraal op te lossen zou zijn om macht te ontwikkelen, zoals werd gedaan in voorbeeld D. Aangezien de exponent echter hoger is, zou het nodig zijn om een ​​variabele wijziging aan te brengen, om niet zo'n lange ontwikkeling te hoeven maken.

Kan u van dienst zijn: continue willekeurige variabele

De variabele verandering is als volgt:

U = x + 7

Aan beide zijden afleiden deze uitdrukking:

du = dx

De integraal wordt getransformeerd naar een eenvoudiger met de nieuwe variabele, die wordt opgelost met de regel van de krachten:

∫ (x+7)⁵ Dx = ∫ u⁵ du = (1/6) u⁶ + C

Ten slotte wordt de wijziging geretourneerd om terug te keren naar de oorspronkelijke variabele:

∫ (x+7)⁵ Dx = (1/6) (x+7)⁶ + C

- Oefening 2

Een deeltje is aanvankelijk in rust en beweegt langs de X -as. De versnelling voor t> 0 wordt gegeven door functie a (t) = cos t. Het is bekend dat bij t = 0 de positie x = 3 is, allemaal in eenheden van het internationale systeem. Er wordt gevraagd om snelheid V (t) te vinden en x (t) van het deeltje te plaatsen.

Oplossing

Aangezien versnelling de eerste is afgeleid van snelheid ten opzichte van de tijd, hebt u de volgende differentiaalvergelijking:

a (t) = v '(t) = cos t

Het volgt dat:

v (t) = ∫ cos t dt = sin t + c₁

Aan de andere kant weten we dat snelheid op zijn beurt de afgeleide van de positie is, daarom integreren we opnieuw:

x (t) = ∫ v (t) dt = ∫ (sin t + c₁) dt = ∫sen t dt + ∫c₁ dt = - cos t + c₁ t + c₂

Integratieconstanten worden bepaald uit de informatie die in de verklaring is gegeven. Ten eerste zegt hij dat het deeltje aanvankelijk in rust was, daarom V (0) = 0:

V (0) = sin 0 + c₁ = 0

C₁ = 0

Dan moet je x (0) = 3:

x (0) = - cos 0 + c₁ 0 + c₂ = - 1 + c₂ = 3 → C₂ = 3+1 = 4

Snelheids- en positiefuncties zijn absoluut zo:

v (t) = sen t

x (t) = - cos t + 4

Referenties

1. Engler, a. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Integrale calculus. Nationale Universiteit van de kust.
2. Larson, r. 2010. Berekening van een variabele. 9NA. Editie. McGraw Hill.
3. Gratis wiskundeteksten. Antiderivatieven. Hersteld van: wiskunde.Liibretexts.borg.
4. Wikipedia. Antiderivatief. Opgehaald uit: in.Wikipedia.borg.
5. Wikipedia. Onbepaalde integratie. Hersteld van: is.Wikipedia.borg.