Gemiddelde versnelling hoe berekend en opgelost oefeningen

De Gemiddelde versnelling naar_M Het is de grootte die de variatie van de snelheid van een deeltje gedurende de tijd beschrijft. Het is belangrijk, omdat het de variaties toont die de beweging ervaart.

Om deze omvang in wiskundige termen uit te drukken, is het noodzakelijk om twee snelheden en twee momenten van tijd te overwegen, die respectievelijk worden aangeduid als V₁ en v₂, en t₁ en t₂.

De gemiddelde versnelling is een zeer belangrijke filmparameter. Bron: Pixabay.

Door de waarden te combineren volgens de aangeboden definitie, zal de volgende uitdrukking worden genomen:

In het internationale systeem als de eenheden voor een_M wordt m/s², Hoewel andere eenheden met een lengte per eenheid van tijd kwadraat zullen dienen.

Bijvoorbeeld is km/h.s die "kilometer per uur en voor de tweede" leest. Merk op dat de tijdseenheid twee keer verschijnt. Als je denkt aan een mobiel die langs een rechte lijn beweegt, betekent dit dat de mobiel voor elke tweede verstreken zijn snelheid verhoogt met 1 km/h. Of daalt met 1 km/u voor elke seconde die voorbijgaat.

[TOC]

Versnelling, snelheid en snelheid

Hoewel het wordt geassocieerd met versnelling met een toename van de snelheid, is de waarheid dat het zorgvuldig observeren van de definitie, het blijkt dat elke verandering in snelheid het bestaan ​​van een versnelling impliceert.

En de snelheid verandert niet altijd in grootte. Het kan gebeuren dat de mobiel alleen van richting varieert en uw snelheid constant houdt. Toch is er een versnelling verantwoordelijk voor deze wijziging.

Een voorbeeld hiervan is een auto die een curve geeft met een constante snelheid van 60 km/u. Het voertuig is onderworpen aan een versnelling, die verantwoordelijk is voor het veranderen van de snelheidsrichting zodat de auto de curve volgt. De bestuurder past het toe met behulp van het stuurwiel.

Een dergelijke versnelling is gericht op het midden van het gebogen traject, om de auto er niet uit te laten komen. Ontvang de naam van de versnelling radiaal of normaal. Als de radiale versnelling plotseling niet werd geannuleerd, kon de auto niet langer de curve geven en doorgaan in een rechte lijn.

Kan u van dienst zijn: WIMSHURSST machine: geschiedenis, hoe het werkt en applicaties

Een auto die door een curve gaat, is een voorbeeld van twee -dimensionale beweging, terwijl wanneer hij in een rechte lijn marcheert, zijn beweging één -dimensionaal is. In dit geval is het enige effect van versnelling om de snelheid van de auto te veranderen.

Deze versnelling wordt versnelling genoemd tangentieel. Het is niet exclusief voor de enige -dimensionale beweging. De auto die de curve op 60 km/u geeft, zou tegelijkertijd 70 km/u kunnen versnellen tijdens het nemen van deze. In dit geval moet de bestuurder zowel het stuurwiel als het versnellingspedaal gebruiken.

Als we een -dimensionale beweging beschouwen, heeft de gemiddelde versnelling een geometrische interpretatie vergelijkbaar met die van de gemiddelde snelheid, als een helling van de drooglijn die de curve snijdt in de punten P en Q van de snelheidsgrafiek versus tijd.

Dit is te zien in de volgende figuur:

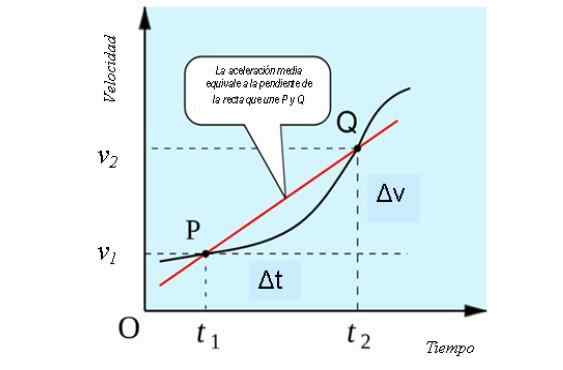Geometrische interpretatie van gemiddelde versnelling. Bron: Bron: すじにく シチュー シチュー [CC0].

Hoe de gemiddelde versnelling wordt berekend

Laten we eens kijken naar enkele voorbeelden om de gemiddelde versnelling in verschillende situaties te berekenen:

I) Op een bepaald moment heeft een mobiel die langs een rechte lijn beweegt een snelheid van + 25 km/u en 120 seconden later heeft nog een van -10 km/u. Wat was de gemiddelde versnelling?

Antwoord

Aangezien de beweging één -dimensionaal is, kan de vectornotatie worden verdeeld met, in welk geval:

v_of = +25 km/h = +6.94 m/s

v_F = -10 km/h = - 2.78 m/s

Δt = 120 s

Wanneer je een oefening hebt met gemengde magnitudes zoals deze, waarin er uren en seconden zijn, is het noodzakelijk om alle waarden aan dezelfde eenheden door te geven.

Omdat het een ene -dimensionale beweging is, is de vectornotatie afgezien van.

Ii) Een fietser beweegt naar het oosten met een snelheid van 2.6 m/s en 5 minuten later gaat naar het zuiden naar 1.8 m/s. Vind de gemiddelde versnelling.

Het kan u van dienst zijn: Vy Canis Majoris: Discovery, Kenmerken, Structuur, Training en Evolutie

Antwoord

De beweging is niet één -dimensionaal, daarom wordt de vectornotatie gebruikt. De eenheidsvectoren Je En J Ze geven de adressen aan naast het volgende tekenconventie, waardoor de berekening wordt vergemakkelijkt:

• Noorden: +J
• Zuiden: -J
• Dit: +Je
• West: -Je

v₂ = - 1.8 J Mevr

v₁ = + 2.6 Je Mevr

Δt = 5 minuten = 300 seconden

De versnelling tekent in de ene -dimensionale beweging

Zoals altijd wat er gebeurt met de gemiddelde of gemiddelde magnitudes, is de verstrekte informatie wereldwijd. Ze bieden geen details over wat er op elk moment met de mobiel is gebeurd, maar wat ze bijdragen blijft waardevol voor de beschrijving van de beweging.

Door zowel tekenen van snelheid als versnelling is het mogelijk om te weten of een mobiel die op een lijn beweegt versnelt of remmen. In beide situaties is de versnelling aanwezig, omdat de snelheid verandert.

Dit zijn enkele interessante overwegingen met betrekking tot de tekenen van deze twee magnitudes:

• Gemiddelde snelheid en versnelling, beide van hetzelfde teken, betekent dat het globaal gezien wordt, de mobiel wordt sneller en sneller.
• Snelheid en versnelling met verschillende tekenen is een teken van een mobiel is ondertekend.

Meestal wordt gedacht dat wanneer het een negatieve versnelling is, de mobiel remmen. Dit is waar als de mobiele snelheid positief is. Maar als het negatief is, neemt de snelheid in feite toe.

Zoals altijd wanneer de beweging wordt bestudeerd, worden speciale gevallen gedacht. Wat er bijvoorbeeld gebeurt als de gemiddelde versnelling nul is?. Betekent het dat de mobiel altijd zijn constante snelheid heeft gehandhaafd?

Het antwoord is nee. De mobiel had zijn snelheid in het overwogen interval kunnen variëren, maar de initiële snelheid en de finale waren hetzelfde. Op dit moment is het detail van wat er in het interval is gebeurd onbekend, omdat de gemiddelde versnelling niet meer informatie biedt.

Kan u van dienst zijn: Joule -effect: uitleg, voorbeelden, oefeningen, toepassingen

Wat als de gemiddelde versnelling naar_M Het is gelijk aan versnelling naar Op elk moment in het tijdelijke interval? Dit is een zeer interessante situatie genaamd rechtlijnige beweging uniform gevarieerd of MRUV).

Betekent dat snelheid na verloop van tijd gelijkmatig verandert. Daarom is de versnelling constant. In de natuur is er zo'n beweging, waarmee iedereen bekend is: vrije val.

Vrije val: een beweging met constante versnelling

Het is een bekend feit dat de aarde objecten naar het midden aantrekt en dat het door sommigen op een bepaalde hoogte vrij te geven, de versnelling van de zwaartekracht, waarvan de waarde ongeveer constant is en gelijk is aan 9.8 m/s² nabij het oppervlak.

Als luchtweerstand niet ingrijpen, is de beweging verticaal en staat bekend als vrije val. Wanneer de versnelling constant is en T kiest₀ = 0, de gemiddelde versnellingsvergelijking wordt omgezet in:

Waarbij een goed bekende formule wordt verkregen om de snelheid te vinden op elk moment van de val:

v_F = V₀ + Op = gt (v₀= 0)

Waar a = g = 9.8 m/s²

Oefening opgelost

Een object wordt van voldoende hoogte gevallen. Vind de snelheid na 1.25 seconde.

Antwoord

v_of = 0, omdat het object wordt gevallen, dan:

v_F = Gt = 9.8 x 1.25 m/s = 12.25 m/s, verticaal gericht naar de grond. (De verticale richting is als positief verwijderd).

Naarmate het object de grond nadert, neemt de snelheid de snelheid toe met 9.8 m/s voor elke tweede verstreken. De massa van het object is er niet bij betrokken. Twee verschillende objecten, gevallen van dezelfde hoogte en ontwikkelen tegelijkertijd dezelfde snelheid als ze vallen.

Referenties

1. Giancoli, D. Natuurkunde. Principes met toepassingen. Zesde editie. Prentice Hall. 21-35.
2. Resnick, r. (1999). Fysiek. Deel 1. Derde editie in het Spaans. Mexico. Continental Editorial Company s.NAAR. van C.V. 20-34.
3. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7^ma. Editie. Mexico. Cengage Learning Editors. 21-39.