Areolaire snelheid hoe het wordt berekend en opgelost oefeningen

De Areolaire snelheid Het is het vegende gebied per tijdseenheid en is constant. Het is typerend voor elke planeet en komt voort uit de beschrijving van Kepler's tweede wet op de wiskundige manier. In dit artikel zullen we uitleggen waar het uit bestaat en hoe het wordt berekend.

De boom die de ontdekking van planeten buiten het zonnestelsel vertegenwoordigt, heeft de interesse in de planetaire beweging opnieuw geactiveerd. Niets gelooft dat deze exo-planets andere wetten volgen dan die al bekend en geldig van het zonnestelsel: de wetten van Kepler.

Johannes Kepler was de astronoom die, zonder de hulp van de telescoop en de observaties van zijn mentor Tycho Brahe gebruikte, een wiskundig model creëerde dat de beweging van de planeten rond de zon beschrijft.

Hij liet dit model uit de drie wetten die zijn naam dragen en die vandaag zo geldig blijven als in 1609, toen hij de eerste twee en 1618 oprichtte, datum waarop de derde.

[TOC]

Kepler -wetten

In de huidige taal zeggen de drie wetten van Kepler als deze:

1. De banen van alle planeten zijn elliptisch en de zon is in een focus.

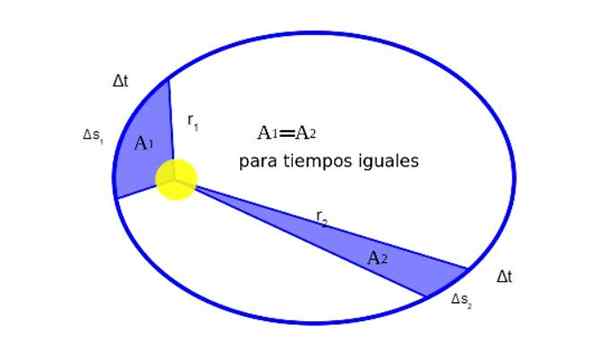
2. De positievector die van de zon naar een planeet gaat, veegt gelijke gebieden in gelijke tijden.

3. Het kwadraat van de orbitale periode van een planeet is evenredig met de kubus van de semi-weise van de beschreven ellips.

Een planeet zal een lineaire snelheid hebben, zoals elk bekend object dat beweegt. En er is meer: ​​bij het schrijven van Kepler's tweede wet in wiskundige vorm, ontstaat een nieuw concept genaamd Areolar Speed, typisch voor elke planeet.

Waarom bewegen planeten elliptisch rond de zon??

De aarde en de andere planeten bewegen zich rond de zon. Hetzelfde geldt voor een andere ster en de planeten die zich aan uw systeem conformeren, als u ze hebt.

Het kan u van dienst zijn: gevoelige hitte: concept, formules en oefeningen opgelost

Dit is een kracht van het type dat bekend staat als centrale kracht. Het gewicht is een centrale kracht waarmee iedereen bekend is. Het object dat de centrale kracht uitoefent, of het nu de zon of een verre ster is, trekt de planeten naar hun centrum en ze bewegen een gesloten curve.

In principe kan deze curve worden benaderd als een omtrek, zoals Nicolás Copernico, een Poolse astronoomschepper van de heliocentrische theorie, deed.

Verantwoordelijke kracht is zwaartekrachtaantrekking. Deze kracht hangt rechtstreeks af van de massa van de ster en de planeet in kwestie en is omgekeerd evenredig met het kwadraat van de afstand die hen scheidt.

Het probleem is niet zo eenvoudig, want in een zonnestelsel werken alle elementen op deze manier op, waardoor complexiteit aan de materie wordt toegevoegd. Het zijn ook geen deeltjes, omdat sterren en planeten meetbare grootte hebben.

Om deze reden is het centrale punt van de baan of circuit die door de planeten wordt afgelegd niet precies gecentreerd op de ster, maar op een punt dat bekend staat als het zwaartepunt van het sol-planet-systeem.

De resulterende baan is elliptisch. De volgende afbeelding toont het, als voorbeeld de aarde en de zon:

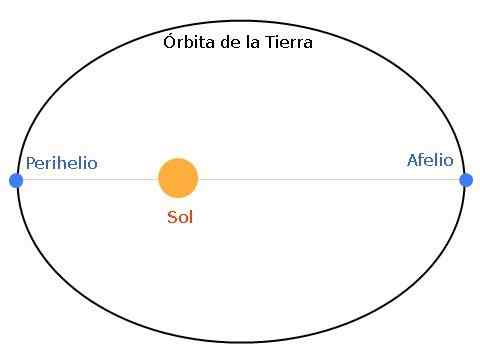Figuur 1. De baan van de aarde is elliptisch, met de zon in een van de foci. Wanneer de aarde en de zon zich op maximale afstand bevinden, wordt gezegd dat de aarde in het aphel is. En als de afstand minimaal is, praten we over Perihelio.

Het apelium is de verste positie van aarde tot de zon, terwijl het perihelium het dichtst in de buurt is. De ellips kan min of meer worden afgeplat, volgens de kenmerken van het sterrensysteem - planeet.

De waarden en perihelio -waarden variëren jaarlijks, omdat de andere planeten verstoringen veroorzaken. Voor andere planeten worden deze posities respectievelijk ondersteuning en expertise genoemd.

De omvang van de lineaire snelheid van een planeet is niet constant

Kepler ontdekte dat wanneer een planeet rond de zon draait, tijdens zijn Barr -beweging gelijk aan gebieden in gelijke tijden. Figuur 2 toont grafisch de betekenis hiervan:

Het kan u van dienst zijn: wat is de balans van het deeltje? (Met voorbeelden)Figuur 2. De positievector van een planeet ten opzichte van de zon is r. Wanneer de planeet beschrijft zijn baan reist een ellipse boog δs in een tijd Δt.

Wiskundig, het feit dat₁ gelijk zijn aan₂ Het wordt zo uitgedrukt:

De bogen routes zijn klein, zodat elk gebied dat van een driehoek kan benaderen:

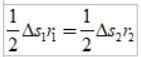
Als δs =vΔT, Waar V de lineaire snelheid van de planeet op een bepaald punt is, hebben we bij het vervangen:

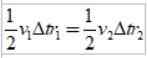
En omdat het tijdsinterval AT hetzelfde is, wordt het verkregen:

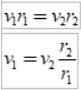
Zoals r₂ > R₁, dan v₁ > v₂, Met andere woorden, de lineaire snelheid van een planeet is niet constant. In feite gaat de aarde sneller wanneer hij zich in het perihelium bevindt dan wanneer hij in het aphel is.

Daarom is de lineaire snelheid van de aarde of een andere planeet rond de zon geen omvang die dient om de beweging van de genoemde planeet te karakteriseren.

Areolaire snelheid

Kepler's tweede wet suggereert een nieuwe omvang genaamd Areolar Speed. Het wordt gedefinieerd als het gebied per tijdseenheid veegde en constant is. Om het te berekenen, wordt het volgende cijfer gebruikt:

figuur 3. De positievector van de aarde (of planeet) ten opzichte van de zon is R, en bij het bewegen is de aarde een verplaatsing, ook vector Δr.

Een klein gebied geveegd door de aarde wordt gekozen tijdens het uitvoeren van zijn elliptische circuit, waarvan we zullen aangeven hoe ΔA. De tijd die hiervoor nodig is, is AT.

Figuur 3 toont de positievector van de aarde ten opzichte van de zon, aangeduid door r. Wanneer de aarde beweegt, ervaar dan een verplaatsing Δr.

Dit gebied komt overeen met de helft van het rechthoekige gebied getoond in figuur 3:

Het quotiënt Δr/Δt is precies de lineaire snelheid van de aarde, dus de teolaire snelheid blijft bestaan:

V_NAAR In het internationale systeem zijn ze:

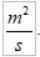
Merk op dat hoewel zowel R als V variëren, het product constant blijft. Dit verandert de areolaire snelheid in een zeer geschikte omvang om de beweging van een planeet rond zijn ster te karakteriseren.

Kan u van dienst zijn: Antoine -constanten: formules, vergelijkingen, voorbeelden

Het product van R en V is de grootte van het hoekmomentum L, zodat de teolaire snelheid kan worden uitgedrukt als:

Het berekenen van lineaire snelheid en een areolaire snelheid

Met het volgende voorbeeld zullen we laten zien hoe we de telaire snelheid kunnen berekenen wanneer sommige parameters van de planetaire beweging bekend zijn:

Oefening

Een exo-planet beweegt rond zijn zon na een elliptische baan, volgens de wetten van Kepler. Wanneer het in de expertro is, is de radiovector r₁ = 4 · 10⁷ km, en wanneer het in de ondersteuning is, is r₂ = 15 · 10⁷ km. De lineaire snelheid in zijn expertise is V₁ = 1000 km/s.

Berekenen:

A) De omvang van de snelheid in de steun.

B) De areolaire snelheid van het exo-planet.

C) De lengte van de ellips grote semi -as.

Antwoord op)

De vergelijking wordt gebruikt:

waarin numerieke waarden worden vervangen.

Elke term wordt als volgt geïdentificeerd:

v₁ = Snelheid in ondersteuning; v₂ = Snelheid in de expert; r₁= Auteur afstand,

R₂= Afstand van de expert.

Met deze waarden wordt het verkregen:

Antwoord b)

De te gebruiken vergelijking is

waarin de paar waarden R en V van de expertro of de ondersteuning kunnen worden vervangen, omdat V_NAAR Het is een planeetconstante:

Antwoord c)

De lengte van de grote semi -as van de ellips is de semi -Semi -semi -semi -semi -seismum en de expertise:

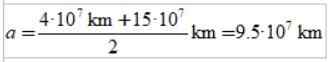
Bibliografie

1. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. Mexico. Cengage Learning Editors. 367-372.
2. Stern, D. (2005). De drie Kepler -wetten van de planetaire beweging. Opgehaald van PWG.GSFC.pot.Gov
3. Opmerking: de voorgestelde oefening is genomen en gewijzigd uit de volgende tekst van een McGrawhill -boek. Helaas is het een geïsoleerd hoofdstuk in het PDF -formaat, zonder de titel of de auteur: Mheducation.Es/bcv/gids/hoofdstuk/844817027X.PDF