Definitie van niet -coplanaire vectoren, voorwaarden, oefeningen

De Niet -coplanares vectoren Zij zijn degenen die niet hetzelfde vliegtuig delen. Twee vrije vectoren en één punt definiëren een enkel vlak. Een derde vector kan dat vlak al dan niet delen en als dit niet het geval is, zijn dit niet -coplanaire vectoren.

Niet -couplet vectoren kunnen niet worden weergegeven in twee -dimensionale ruimtes zoals een bord of een vel papier, omdat sommige daarvan in de derde dimensie zijn opgenomen. Om ze goed te vertegenwoordigen, moet u perspectief gebruiken.

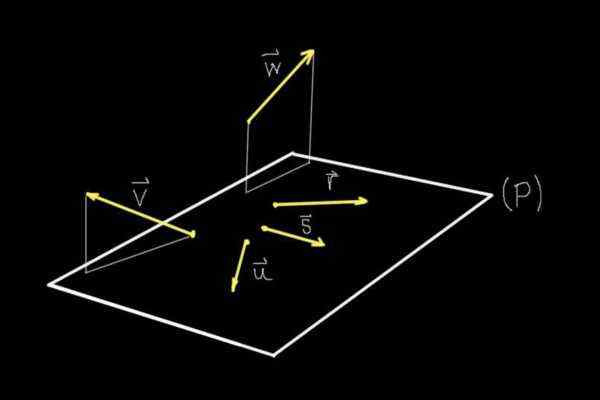Figuur 1. Coplanares en niet-koppelingsvectoren. (Eigen uitwerking)

Als we figuur 1 observeren, zijn alle strikt getoonde objecten in het vlak van het scherm, maar dankzij het perspectief kan ons brein zich een vlak (p) voorstellen dat uit hetzelfde komt.

Op dat vlak zijn (P) de vectoren R, S, of, Terwijl vectoren v En W  Ze zitten niet in dat vliegtuig.

Daarom de vectoren R, S, of Ze zijn coplanarios of coplanares met elkaar omdat ze hetzelfde vlak delen (p). De vectoren v En W Ze delen geen flat met een van de andere getoonde vectoren, daarom zijn ze niet-koppeling. 

[TOC]

Coplanares en vliegtuigvergelijkingsvectoren

Een vlak is uniek gedefinieerd als er drie punten worden gegeven in de drie -dimensionale ruimte.

Stel dat die drie punten het punt zijn NAAR, punt B En het punt C die het vlak definiëren (P). Met deze punten is het mogelijk om twee vectoren te bouwen AB = U En AC = V die door constructie zijn met het vliegtuig (P).

Het vectorproduct (of kruisproduct) van deze twee vectoren resulteert in een derde loodrechte (of normale) vector en daarom loodrecht op het vlak (P):

n = u X v   => N ⊥ of  En N ⊥ v   => N ⊥ (P)    

Kan u van dienst zijn: gewicht (fysiek): berekening, eenheden, voorbeelden, oefeningen

Elk ander punt dat bij het vliegtuig hoort (P) Moet die vector vervullen Aq loodrecht op de vector staan N; Dit is gelijk aan te zeggen dat het scalaire product (of puntproduct) van N met Aq Het moet nul zijn:

N • Aq = 0 (*)

De vorige voorwaarde is gelijk aan te zeggen dat:

Aq • (of X v) = 0 

Deze vergelijking zorgt ervoor dat het punt Q behoren tot het vliegtuig (P). 

Cartesiaanse vergelijking van het vlak

De vorige vergelijking kan op Cartesiaanse manier worden geschreven. Hiervoor schrijven we de coördinaten van de punten NAAR, Q en de componenten van de normale vector N:

A = (a, b, c)

Q = (x, y, z)

N= (NX, NY, NZ)

Zodat de AQ -componenten zijn:

Aq= (X-A, Y-B, Z-C)

De voorwaarde voor de vector Aq in het vliegtuig worden opgenomen (P) Het is de voorwaarde (*) die nu als volgt is geschreven:

(NX, NY, NZ) • (X-A, Y-B, Z-C) = 0

Het berekenen van het puntproduct blijft bestaan:

NX (X-A) + NY (Y-B) + NZ (Z-B) = 0

Als het zich ontwikkelt en herschikt, blijft het:

NX X + NY Y + NZ Z = NX A + NY B + NZ C

De vorige uitdrukking is de Cartesiaanse vergelijking van een vlak (P), afhankelijk van de componenten van een normale vector tot (P) en de coördinaten van een punt NAAR die tot (P).

Voorwaarden voor drie vectoren om niet -coplanares te zijn

Zoals de voorwaarde is gezien in de vorige sectie Aq • (of X v) = 0 garandeert dat de vector Aq Het is coplanario a of En v.

Als we bellen W naar de vector Aq Dan kunnen we dat bevestigen:

W, of En v Het zijn coplanares, ja en alleen als W • ( of X v ) = 0.

Toestand van niet-gedragigheid

Als het drievoudige (of gemengde product) product van drie vectoren verschilt van nul, dan zijn die drie vectoren niet-dekten.

Het kan u van dienst zijn: Politropisch proces: kenmerken, toepassingen en voorbeelden

Ja    W • ( of X v ) ≠ 0 dan zijn de U-, V- en W-vectoren niet-couplanarios.

Als de Cartesiaanse componenten van de U, V, V en W worden geïntroduceerd, kan de toestand van niet-gedrag als volgt worden geschreven:

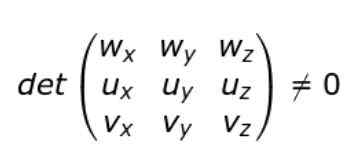Dat wil zeggen dat als de bepalende factor van de matrix (3 × 3) wiens rijen de componenten van de U-, V- en W-vectoren zijn, de vectoren niet-koppeling zijn.

Het drievoudige product heeft een geometrische interpretatie en vertegenwoordigt het volume van de parallellepiped gegenereerd door de drie niet -coplanares vectoren.

Figuur 2. Drie niet-koppelingsvectoren definiëren een parallellepipedo waarvan het volume de drievoudige productmodule is. (Eigen uitwerking)

De reden is als volgt; Wanneer twee van de niet-koppelingsvectoren zich vermenigvuldigen. 

Wanneer deze vector dan vermenigvuldigt is. 

Met andere woorden, u hebt het parallellogramgebied gegenereerd door de eerste twee vermenigvuldigd met de hoogte van de derde vector.

Alternatieve toestand van niet-koppeling

Als je drie vectoren hebt en een van hen niet kan worden geschreven als een lineaire combinatie van de andere twee, dan zijn de drie vectoren niet-dekten. Dat zijn drie vectoren of, v En W Ze zijn niet-dekten als de toestand:

α of + β v + γ W = 0

Het wordt alleen vervuld wanneer α = 0, β = 0 en γ = 0.

Opgeloste oefeningen

-Oefening 1

Je hebt drie vectoren

of = (-3, -6, 2);   v = (4, 1, 0) en W = (-1, 2, z)

Merk op dat de Z -component van de vector W Het is onbekend.

Zoek het bereik van waarden dat Z kan nemen, zodat gegarandeerd is dat de drie vectoren niet hetzelfde vlak delen.

Kan u van dienst zijn: stabiele balans: concept en voorbeelden

Oplossing 

We passen opnieuw het criterium van de bepalende factor van de matrix uit die door de rangen van de drie vectoren zijn gevormd, op deze manier blijven we: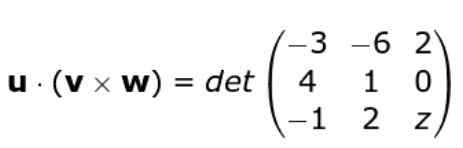We ontwikkelen de determinant

W • ( of X v ) = -3 (z - 0) + 6 (4 z - 0) + 2 (8 + 1) = -3Z + 24Z + 18 = 21z + 18

We matchen deze uitdrukking op nulwaarde

21 z + 18 = 0

en we wissen Z

Z = -18/21 = -6/7

Als de variabele z de waarde -6/7 zou nemen, zouden de drie vectoren coplanares zijn.

Zodat de waarden van z die garanderen dat de vectoren niet-dekten zijn die in het volgende interval zijn:

Z ∈ (-∞, -6/7) u (-6/7, ∞)

-Oefening 2

Zoek het volume van de parallellepiped getoond in de volgende figuur:

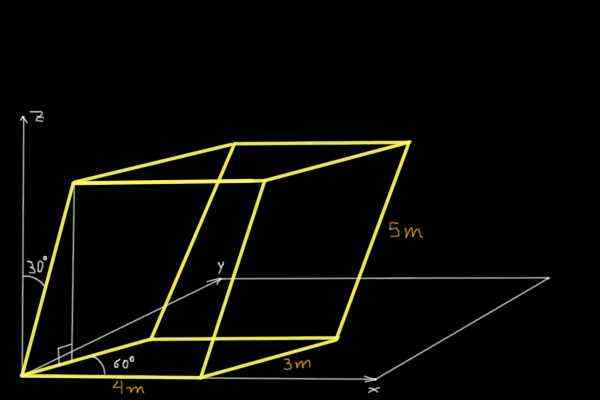
Oplossing 

Om het volume van de parallellepiped te vinden die in de figuur wordt getoond, worden de Cartesiaanse componenten van drie niet-concurrent niet-koppelingsvectoren bepaald in de oorsprong van het coördinatensysteem. De eerste is de vector of  4m en parallel aan de X -as:

of= (4, 0, 0) m

De tweede is de vector v In het XY 3M -maatvlak dat 60º vormt met de x -as:

v= (3*cos 60º, 3*sen 60º, 0) = (1.5, 2.6, 0.0) M

En de derde de vector W van 5 m en wiens projectie in het xy -vlak 60º vormt met de x -as, bovendien wenst w 30º met de z -as.

W= (5*sin 30º*cos 60º, 5*sen 30º*sin 60º, 5*sen 30º)

Voer de berekeningen uit die we hebben: W= (1.25, 2.17, 2.5m.

Referenties

1. Figueroa, D. Serie: Physics for Science and Engineering. Deel 1. Kinematica. 31-68.
2. Fysiek. Module 8: vectoren. Hersteld van: frtl.Utn.Edu.AR
3. Hibbeler, R. 2006. Mechanica voor ingenieurs. Statisch. 6e editie. Continentaal redactioneel bedrijf.28-66.
4. McLean, W. Schaum -serie. Mechanica voor ingenieurs: statisch en dynamisch. 3e editie. McGraw Hill. 1-15.
5. Wikipedia. Vector. Hersteld van: het is.Wikipedia.borg