Relatief snelheidsconcept, voorbeelden, oefeningen

De Relatieve snelheid van een object is er een die wordt gemeten met betrekking tot een bepaalde waarnemer, omdat een andere waarnemer een andere maat kan verkrijgen. De snelheid hangt altijd af van de waarnemer die het meet.

Daarom zal de snelheid van een object gemeten door een bepaalde persoon de relatieve snelheid zijn met betrekking tot het. Een andere waarnemer kan een andere waarde verkrijgen voor de snelheid, nog steeds in het geval van hetzelfde object.

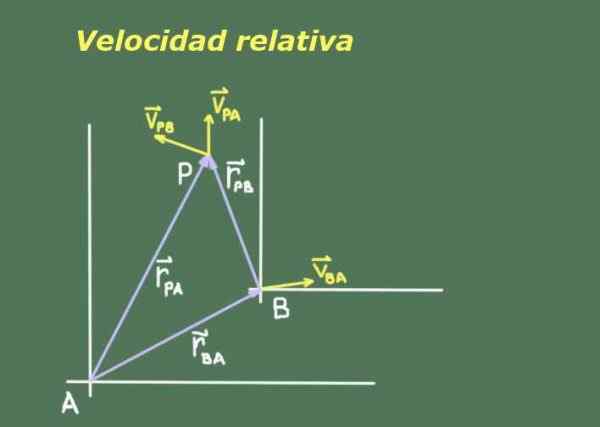
Figuur 1. Schema dat tot het punt P in beweging vertegenwoordigt, gezien uit referentiesystemen A en B. Bron: zelf gemaakt.

Aangezien twee waarnemers A en B die van elkaar bewegen, kunnen ze verschillende maatregelen hebben van een derde P -object dat beweegt, is het noodzakelijk om te zoeken naar een relatie tussen de posities en snelheden van P -weergaven door A en B.

Figuur 1 toont twee waarnemers A en B met hun respectieve referentiesystemen, waaruit ze de positie en snelheid van object P meten.

Elke waarnemer A en B meet de positie en snelheid van object P op een bepaald tijdstip T. In de klassieke relativiteit (of Galilea) is de tijd voor waarnemer A hetzelfde als voor waarnemer B, ongeacht de relatieve snelheden.

Dit artikel gaat over klassieke relativiteitstheorie die geldig is en van toepassing is op de meeste dagelijkse situaties waarin objecten veel lagere snelheden hebben dan die van licht.

De positie van waarnemer B met betrekking tot de aanduidingen als R_Ba. Omdat de positie een vectorhoeveelheid is, gebruiken we BOLD om dit aan te geven. De positie van object P ten opzichte van een aangegeven als R_vader en dat van hetzelfde object P met betrekking tot B R_PB.

[TOC]

Relatie tussen posities en relatieve snelheden

Er is een vectorrelatie tussen deze drie posities die kunnen worden afgeleid uit de weergave van figuur 1:

 R_vader= R_PB + R_Ba

Als de vorige uitdrukking wordt genomen met betrekking tot de tijd T We zullen de relatie verkrijgen tussen de relatieve snelheden van elke waarnemer:

U kunt u van dienst zijn: de tweede wet van Newton: aanvragen, experimenten en oefeningen

V_vader= V_PB + V_Ba

In de vorige uitdrukking is er de relatieve snelheid van P ten opzichte van A, afhankelijk van de relatieve snelheid van P ten opzichte van B en de relatieve snelheid van B ten opzichte van B.

Evenzo kan de relatieve snelheid van P worden geschreven met betrekking tot de relatieve snelheid van P ten opzichte van A en de relatieve snelheid van B.

V_PB= V_vader + V_Aab

Opgemerkt moet worden dat de relatieve snelheid van B is gelijk en in tegenstelling tot die van B ten opzichte van A:

V_Aab = -V_Ba 

Dit wordt gezien door een kind uit een bewegende auto

Een auto gaat langs een rechte weg, die van west naar dit gaat, snel vanaf 80 km/u terwijl in de tegenovergestelde richting (en op de andere rijstrook) een motorfiets snel 100 km/u komt.

Op de achterbank van de auto reist een kind dat de relatieve snelheid van een motorfiets wil weten die hem nadert. Om het antwoord te achterhalen, past het kind de relaties die u zojuist hebt gelezen in de vorige sectie toe en identificeert elk coördinatensysteem als volgt:

-A is het coördinatensysteem van een waarnemer op de weg en met betrekking tot het zijn de rapides van elk voertuig gemeten.

-B is de auto en P zal de motorfiets zijn.

Als u de snelheid van de Moto P met betrekking tot auto B wilt berekenen, wordt de volgende relatie toegepast:

V_PB= V_vader + V_Aab=V_vader - V_Ba

Zo positief de westoostelijke richting die je hebt:

V_PB= (-100 km/u - 80 km/u) Je = -180 km/h Je

Dit resultaat wordt als volgt geïnterpreteerd: de motorfiets beweegt ten opzichte van de auto met een snelheid van 180 km/u en richting -Je, Dat wil dit tegen West zeggen.

Het kan u van dienst zijn: Block Algebra: Elementen, voorbeelden, opgeloste oefeningen

Relatieve snelheid tussen de motorfiets en de auto

De motorfiets en de auto zijn ze allemaal overgestoken na hun rijstrook. De jongen die op de achterbank van de auto gaat, ziet de motorfiets weg en wil nu weten met welke snelheid hij van hem weggaat, ervan uitgaande dat zowel motorfiets als auto dezelfde Rapides behouden als voorover het kruist.

Om het antwoord te weten, past het kind dezelfde relatie toe die eerder werd gebruikt:

V_PB= V_vader + V_Aab=V _vader - V_Ba

V_PB= -100 km/h Je - 80 km/h Je = -180 km/h Je

En nu beweegt de motorfiets weg van de auto met dezelfde relatieve snelheid waarmee ze naderden voordat ze overstaken.

Dezelfde motorfiets van deel 2 keert terug door de dezelfde snelheid van 100 km/u te behouden maar het adres te wijzigen. Dat wil zeggen de auto (die snel 80 km/u doorgaat) en de motorfiets beweegt beide in een positieve richting.

Op een gegeven moment overtreft de motorfiets de auto en het kind dat op de achterbank van de auto gaat, wil de relatieve snelheid van de motorfiets met betrekking tot hem weten wanneer hij haar aan haar zijde ziet passeren.

Om het antwoord te verkrijgen, past het kind opnieuw de relaties van de relatieve beweging toe:

V_PB= V_vader + V_Aab=V_vader - V_Ba

V_PB= +100 km/h Je - 80 km/h Je = 20 km/h Je 

Het kind vanaf de achterbank observeert de motorfiets die de auto oploopt met een snelheid van 20 km/u.

-Oefening opgelost

Oefening 1

Een motorboot kruist een rivier van 600 m breed en stroomt van noord naar zuid. De snelheid van de rivier is 3 m/s. De bootsnelheid ten opzichte van het rivierwater is 4 m/s in het oosten.

Kan u van dienst zijn: takken van klassieke en moderne fysica

(i) Vind de bootsnelheid ten opzichte van de rivieroever.

(ii) Geef de snelheid en richting van de boot aan ten opzichte van het land aan.

(iii) Bereken de kruisingstijd.

(iv) Hoeveel zal er naar het zuiden zijn verhuisd ten opzichte van het startpunt.

Oplossing 

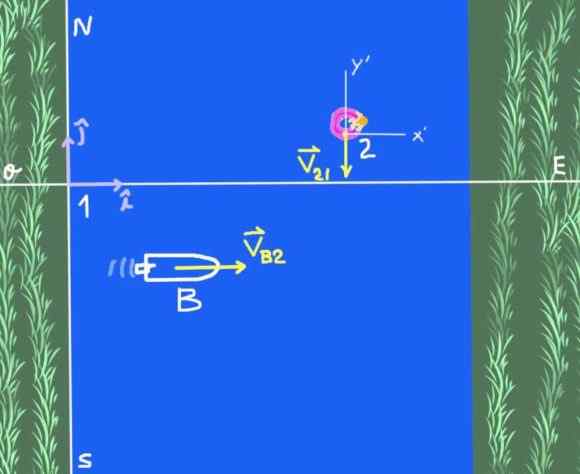Figuur 2. Boot die de rivier oversteekt (oefening 1). Bron: zelf gemaakt.

Er zijn twee referentiesystemen: het Solidariteitsreferentiesysteem bij de Riverbank dat we 1 en het referentiesysteem 2 zullen bellen dat een waarnemer is die op het rivierwater zweeft. Het object van de studie is boot B.

De snelheid van de boot ten opzichte van de rivier is als volgt in een vectorvorm geschreven:

VB2 = 4 Je Mevr

De snelheid van waarnemer 2 (vlot over de rivier) ten opzichte van waarnemer 1 (op land):

Veenentwintig = -3 J Mevr

U wilt de bootsnelheid vinden met betrekking tot land VB1.

VB1 = VB2 + Veenentwintig

Antwoord i

VB1 = (4 Je - 3 J) Mevr   

De snelheid van de boot zal de vorige snelheidsmodule zijn:

|VB1| = (42 + (-3) 2) ½ = 5 m/s

Antwoord II

En het adres zal zijn:

θ = arcan (-¾) = -36,87º 

Antwoord III

De kruisingstijd van de boot is de verhouding tussen de breedte van de rivier en de component X van de bootsnelheid ten opzichte van de aarde.

t = (600 m)/(4 m/s) = 150 s 

Antwoord IV

Om de drift te berekenen die de boot in het zuiden had, worden de component en de snelheid van de boot ten opzichte van de grond vermenigvuldigd met de oversteektijd:

D = -3 J m/s * 150 s = -450 J M

De verplaatsing naar het zuiden ten opzichte van het startpunt is 450m.

Referenties

1. Giancoli, D. Natuurkunde. Principes met toepassingen. 6e editie. Prentice Hall. 80-90
2. Resnick, r. (1999). Fysiek. Deel 1. Derde editie in het Spaans. Mexico. Continental Editorial Company s.NAAR. van C.V. 100-120.
3. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. Editie. Mexico. Cengage Learning Editors. 95-100.
4. Wikipedia. Relatieve snelheid. Hersteld van: Wikipedia.com
5. Wikipedia. Relatieve snelheidsmethode. Hersteld van: Wikipedia.com