Definitie van de equipoale vectoren, notatie, oefeningen

Twee of meer Vectoren zijn apparatuur Als ze dezelfde module hebben, dezelfde richting en gelijkwaardige zin, zelfs wanneer hun punt van oorsprong anders is. Vergeet niet dat de kenmerken van een vector precies zijn: oorsprong, module, richting en zin. 

Vectoren worden vertegenwoordigd door een georiënteerd of pijlsegment. Figuur 1 toont de weergave van verschillende vectoren in het vlak, waarvan sommige apparatuur zijn volgens de aanvankelijk gegeven definitie.

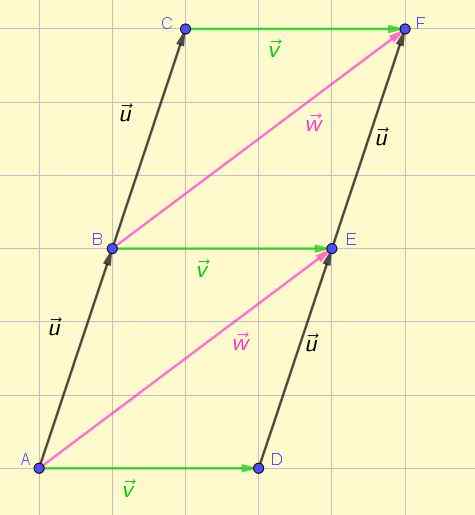Figuur 1. Apparatuur en niet -afgestemde vectoren. Bron: zelf gemaakt.

Vanaf het eerste gezicht is het mogelijk om te waarderen dat de drie groene vectoren dezelfde grootte hebben, dezelfde richting en dezelfde zin. Hetzelfde kan worden bevestigd over de twee roze vectoren en de vier zwarte vectoren.

Talrijke natuurgroeven hebben een vectorgedrag, dat is het geval van snelheid, versnelling en sterkte, om slechts enkele te noemen. Vandaar het belang van het goed karakteriseren van hen.

[TOC]

Notatie voor vectoren en apparatuur

Om de vectorhoeveelheden van de scalaire hoeveelheden te onderscheiden, wordt de zwarte -type letter of een pijl op de letter vaak gebruikt. Bij het werken met handvectoren, op het notitieboekje, is het noodzakelijk om ze te onderscheiden met de pijl en wanneer een bedrukt medium wordt gebruikt, worden gewaagde.

Vectoren kunnen worden ontkend dat hun startpunt of oorsprong en hun aankomstpunt aangeven. Bijvoorbeeld Aab, BC, VAN En EF van figuur 1 zijn echter vectoren Aab, BC, VAN En EF Het zijn scalaire hoeveelheden of getallen die de grootte, module of grootte van hun respectieve vectoren aangeven.

Om aan te geven dat twee vectoren apparatuur zijn, wordt het symbool gebruikt "∼ ". Met deze notatie kunnen we in de figuur wijzen op de volgende vectoren die apparatuur met elkaar zijn:

Kan u van dienst zijn: kinetische energie: kenmerken, typen, voorbeelden, oefeningen

AB∼BC∼DE∼EF 

Ze hebben allemaal dezelfde omvang, richting en betekenis. Voldoen daarom aan de hierboven aangegeven voorschriften.

Gratis, glijdende en tegengestelde vectoren

Een van de vectoren in de figuur (bijvoorbeeld Aab) is een vertegenwoordiger van de set van alle vaste vaste vectoren. Deze oneindige set definieert de klasse van vrije vectoren of.

of = AB, BC, van, ef, ..

Een alternatieve notatie is als volgt:

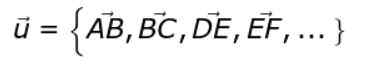
Als de vetgedrukte of pijl niet bovenaan wordt geplaatst of, We willen verwijzen naar de vectormodule of.

Gratis vectoren worden niet op een bepaald punt toegepast.

Van hun kant de Glijdende vectoren Het zijn apparatuurapparatuur voor een bepaalde vector, maar hun aanvraagpunt moet in de vectoractielijn worden opgenomen.

En de tegenovergestelde vectoren Het zijn vectoren die dezelfde omvang en richting hebben, maar tegengestelde zintuigen, hoewel ze in Engelse teksten worden genoemd tegenovergestelde adressen Omdat het adres ook de betekenis aangeeft. Tegengestelde vectoren zijn geen apparatuur.

Opdrachten

-Oefening 1

Welke andere vectoren van die getoond in figuur 1 zijn apparatuur met elkaar?

Oplossing

Afgezien van die al aangegeven in de vorige sectie, wordt uit figuur 1 waargenomen dat ADVERTENTIE, Zijn En EC Het zijn ook apparatuur vectoren met elkaar:

Ad ∼ ∼ be ∼ ce 

Elk van hen is een vertegenwoordiger van de klasse van vrije vectoren v.

Vectoren zijn ook apparatuur onderling AE En BF :

Ae ∼ BF 

Die klassenvertegenwoordigers zijn W.

-Oefening 2

Punten A, B en C staan ​​op Cartesiaans XY -vliegtuig en hun coördinaten zijn:

Kan u van dienst zijn: ideaal gas: model, gedrag, voorbeelden

A = (-4.1), b = (-1.4) en c = (-4, -3)

Zoek de coördinaten van een vierde punt D zodat de vectoren Aab En CD Apparatuur zijn.

Oplossing 

Zodat CD Apparatuur zijn Aab moet dezelfde module hebben en dezelfde richting als Aab .

De module van Aab Vierkant is:

|Aab|^2 = (-1 -( -4))^2 + (4 -1)^2 = 9 + 9 = 18

D -coördinaten zijn onbekend om wat we kunnen zeggen: D = (X, Y)

Dan: |CD|^2 = (x -(-4))^2 + (y -( -3))^2

Als |Aab| = |CD| Het is een van de voorwaarden voor Aab En CD Wees apparatuur die je hebt:

(x + 4)^2 + (y + 3)^2 = 18

Aangezien er twee onbekenden zijn, is een andere vergelijking vereist, die kan worden bereikt uit de voorwaarde dat Aab En CD wees parallel en in dezelfde zin.

Vector AB helling

De vectorhelling Aab geeft uw adres aan:

In afwachting van AB = (4 -1)/(-1 -( -4)) = 3/3 = 1

Wat aangeeft dat de vector Aab 45º vorm met de x -as.

CD -vectorhelling

De helling van CD Het wordt op dezelfde manier berekend:

In afwachting van cd = (y -( -3))/(x -(-4)) = (y + 3)/(x + 4)

Het matchen van dit resultaat met de helling van Aab Je hebt de volgende vergelijking:

Y + 3 = x + 4 

Wat betekent y = x + 1.

Als dit resultaat wordt vervangen in de vergelijking van de gelijkheid van de modules, is dit:

(x + 4)^2 + (x + 1 + 3)^2 = 18

Vereenvoudiging is:

2 (x+4)^2 = 18, 

Die gelijkwaardig is aan:

(x+4)^2 = 9

Dat is x+4 = 3 wat inhoudt dat x = -1. Zodat de coördinaten van D zijn (-1, 0).

rekening

Vectorcomponenten Aab ze zijn (-1-(-4); 4 -1) = (3; 3)

Kan u van dienst zijn: Thévenin Stelling: wat bestaat, applicaties en voorbeelden

en die van de vector CD Ze zijn (-1-(-4)); 0 -(-3)) = (3; 3)

Wat betekent dat vectoren apparatuur zijn. Als twee vectoren dezelfde Cartesiaanse componenten hebben, hebben dezelfde module en richting, daarom zijn ze apparatuur.

-Oefening 3

De vrije vector of heeft magnitude 5 en adres 143,1301º.

Vind zijn Cartesiaanse componenten en bepaal de coördinaten van punten B en C wetende dat vaste vectoren AB en CD apparatuur zijn. De coördinaten van A zijn (0, 0) en de coördinaten van punt C zijn (-3,2).

Oplossing 

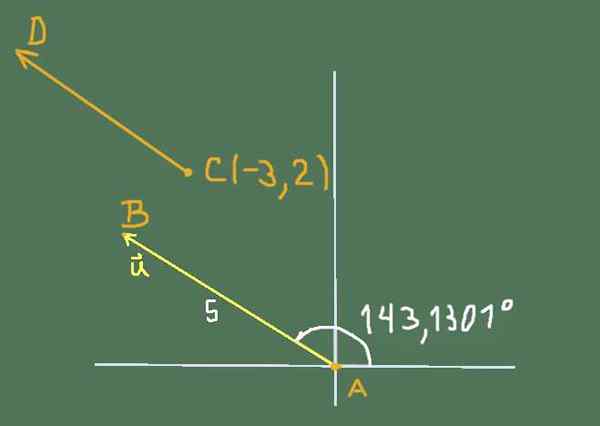
De door de oefening voorgestelde situatie kan worden weergegeven door de volgende figuur:

Figuur 2. Diagram voor de oplossing van oefening 3. Bron: zelf gemaakt.

Cartesiaanse componenten van of Zijn

of = (5*cos (143,1301º); 5*sin (143,1301º)) 

Het maken van de berekeningen blijft:

of = (-4; 3) 

B -coördinaten zijn onbekend, dus we zullen B (X, Y) plaatsen

Vector's coördinaten Aab Ze zijn (x-0; y-0), maar omdat het apparatuur met u is, moet de gelijkheid van componenten worden vervuld, wordt daarom geconcludeerd dat de coördinaten van B zijn (-4, 3).

Evenzo coördineert de vector CD Ze zijn (x-(-3)); (en - 2) dat moet apparatuur zijn u, lof dat leidt tot:

 x + 3 = -4 en y -2 = 3

Dan zullen de coördinaten van punt D zijn (-7, 5).

Referenties

1. Berekening.DC. Vaste vector. Gratis vector. Teruggewonnen uit: berekening.DC
2. 2d Descartes. Vaste vectoren en vrije vectoren van het vliegtuig. Opgehaald uit: bronnen.onderwijs.is
3. Guao -project. Equipoire vectoren. Hersteld van: guao.borg
4. Resnick, r., Krane, k. (2001). Natuurkunde (in het Engels). New York: John Wiley & Sons.
5. Serway, r.; Jewett, John W. (2004). Natuurkunde voor wetenschappers en ingenieurs (in het Engels) (6e editie). Brooks/Cole.
6. Tupler, Paul A. (2000). Natuurkunde voor wetenschap en technologie. Deel I. Barcelona: ED. Ik heb omgekeerd.
7. Weisstein, E. "Vector". In Weisstein, Eric W. Mathworld (in het Engels). Wolfram -onderzoek.