Lineair variatie -concept, voorbeelden, oefening opgelost

De Lineaire variatie Het komt voor tussen twee fysieke magnitudes wanneer de grafiek die ze vertegenwoordigt een rechte lijn is. Het is gelijk aan het bevestigen dat de variabelen in lineaire afhankelijkheid zijn, zodat als een van hen het "y" en de andere "x" noemen, ze worden gerelateerd door wiskundige expressie:

y = mx + b

In deze formule zijn M en B reële getallen. De waarde van M vertegenwoordigt de helling of helling van de lijn - die altijd constant is - en B is de snit van de lijn met de verticale as.

De lineaire variatie van de ene grootte ten opzichte van een andere betekent dat de grafiek een rechte lijn is. Bron: Joulesergio/CC BY-S (https: // creativeCommons.Org/licenties/by-sa/4.0)

Elk fenomeen dat reageert op een lineaire variatie heeft verschillende namen voor de variabelen, zoals we zullen zien in de volgende voorbeelden. De wiskundige vorm van de vergelijking is echter hetzelfde.

Experimenteel kan worden vastgesteld als er een lineair verband is tussen twee magnitudes, die paren van waarden meet (x, y).

De verkregen punten zijn grafisch in een millimeterpapier en worden waargenomen als ze een lineaire trend hebben, dat wil zeggen, als er een lijn is die zich voldoende aanpast aan de experimentele gegevens.

In eerste instantie kan deze lijn visueel worden getrokken, maar door middel van een lineaire regressie Ze zijn analytisch te vinden, de waarden van M en B van de lijn die het beste bij de experimentele punten passen.

[TOC]

Voorbeelden van lineaire variatie

Er zijn tal van natuurlijke fenomenen, evenals gevestigde relaties tussen het meten van patronen, die bijvoorbeeld een lineaire variatie gehoorzamen: bijvoorbeeld:

Snelheid in de uniform gevarieerde rechtlijnige beweging

De snelheid afhankelijk van de tijd V (t) van een mobiel die langs een lijn beweegt met constante versnelling bij en initiële snelheid V_of  anders dan 0. Deze beweging staat bekend als uniform gevarieerde rechtlijnige beweging En de snelheidsvergelijking is:

Kan u van dienst zijn: dichtheid

v (t) = v_of + BIJ

Thermische expansie

Een ander natuurlijk fenomeen waarvan de variatie lineair is, is de toename van de lengte die een staaf of een draad ervaart wanneer verwarmd.

Inderdaad, wanneer de temperatuur van een object toeneemt, is de afmetingen ervan ook en deze toename hangt af van de temperatuurverandering Δt en een hoeveelheid die wordt genoemd lineaire dilatatiecoëfficiënt aangegeven door de Griekse letter α:

L = l_of + α Δt

In deze uitdrukking is L de uiteindelijke lengte van het object en l_of is de beginlengte.

Positie van een mobiel met constante snelheid

Een mobiel met snelheid constant beweegt altijd in een rechte lijn. Als de rechte lijn de horizontale as x is, wordt de positie x (t) op elk moment gegeven door:

x (t) = x_of + VT

Waar x_of Het is de beginpositie, v is de snelheid en t is de tijd. Op deze manier wordt gezegd dat de X -positie lineair varieert met de tijd T.

Een persoon gestateerde

Artsen en antropologen kunnen de status van een persoon schatten door de lengte van het dijbeen te meten.

Hoe hoger een persoon, hoe langer de benen hebben, dus er zijn lineaire modellen om de hoogte van een volwassen persoon h (in inches) te voorspellen als de lengte L (ook in inches) van zijn dijbeen bekend is, volgens de vergelijking:

H = 1.880⋅l + 32.010

Temperatuurschalen

Celsius en Fahrenheit -schalen worden dagelijks gebruikt om de temperaturen te meten. Deze laatste schaal wordt vaak gebruikt in Engelse landen. Er is een gelijkwaardigheid om van de ene naar de andere te gaan:

F = (9/5) C + 32

Waarbij f de temperatuur is in graden fahrenheit en c is de temperatuur in graden Celsius.

Druk en diepte

De absolute druk P in een niet -samendrukbare vloeistof zoals water, waarvan de constante dichtheid ρ is, varieert afhankelijk van de diepte H als:

Het kan u van dienst zijn: horizontaal schieten: kenmerken, formules en vergelijkingen, oefeningen

P = P_of + ρGH

Waar P_of Het is de druk op het vrije oppervlak van de vloeistof. Als de vloeistof zich in een container voor de atmosfeer bevindt, is deze druk gewoon de atmosferische druk p p_Geldautomaat, In staat zijn om dan te schrijven:

P = P_Geldautomaat + ρGH

Atmosferische druk op zeeniveau is ongeveer 101 kPa. Deze relatie tussen P en H betekent dat de druk lineair toeneemt met diepte.

De druk die de duiker ervaart, varieert lineair met diepte. Bron: Ahmed Samy/Pexels.

Oefening opgelost

Rijkosten

De maandelijkse kosten C van het hanteren van een auto omvat een maandelijkse vaste kosten C_of Plus de kosten van kilometers of de kilometerstand reisden elke maand. Een bestuurder merkt op dat de managementkosten in een maand $ 380 waren voor $ 480, en de volgende maand was het $ 460 per 800 mijl.

Laat het aantal mijlen per maand door de bestuurder worden gereisd, met de verstrekte gegevens, vinden:

a) de lineaire variatie tussen C en D.

b) Hoeveel zou de auto per maand kosten op een reis van 1500 mijl?

c) De grafiek van C versus D.

Oplossing voor

Stel dat de variabelen een relatie hebben gegeven door:

C = C_of + NAAR.D

Waar a en c_of Ze zijn constant om te bepalen. A is de helling van de lijn die grafisch de relatie weergeeft tussen C en D. CO is de verlaging met de verticale as, de maandelijkse vaste kosten die de bestuurder moet betalen voor het feit dat de auto beschikbaar is. Hier kunnen onderhoud en belastingkosten bijvoorbeeld worden opgenomen.

Om ondubbelzinnig een lijn te bepalen, is het noodzakelijk om de helling te kennen. Hiervoor hebben we de punten:

P₁: 480 mijl, $ 380

P₂: 800 mijl, $ 460

Deze punten van coördinaten (d, c) of (afstand, kosten) zijn analoog aan de coördinaatpunten (x, y) van het cartesiaanse vlak, welke veranderingen zijn de namen. De helling naar de lijn wordt dan gegeven door:

Kan u van dienst zijn: hellend vlak

A = (c₂ - C₁)/(D₂ - D₁))

A = [(460 - 380) $ / (800 - 480) mijl] = (1/4) $ / mijl

De helling van de lijn vertegenwoordigt de kosten per mijl, op deze manier:

C = C_of + NAAR.D = CO + (1/4).D

Om de basiskosten te bepalen C_of Deze vergelijking wordt genomen en een van de punten die we kennen behoort erbij, bijvoorbeeld p₁:

380 $ = C_of + [(1/4) $ / mijl] . 480 mijl → 380 $ = C_of + $ 120

C_of = $ 260

Nu kunnen we het lineaire variatiemodel formuleren zoals:

C = 260 + (1/4) D

Oplossing B

De maandelijkse kosten van reizen 1500 mijl zijn:

C = 260 + (1/4) x 1500 $ = $ 635

Oplossing C

De grafiek van C als functie van D is:

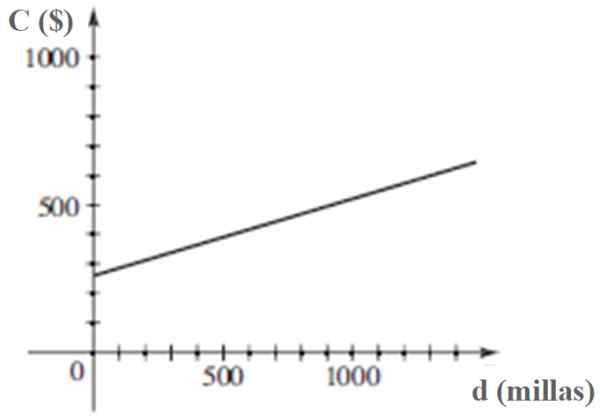De kosten C van het hanteren van een voertuig is een lineaire functie van de afgelegde afstand D D. Bron: Stewart, J. Voorzetting.

Referenties

1. Baldor. 1977. Elementaire algebra. Venezolaanse culturele edities.
2. Hoekenga, c. Lineaire vergelijkingen in de wetenschap. Hersteld van: VisionLearning.com.
3. Hoffman, J. Selectie van wiskundeproblemen. Deel 2.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
6. Zill, D. 1984. Algebra en trigonometrie. McGraw Hill.