Relatieve waarde

Wat is de relatieve waarde van een nummer?

Hij relatieve waarde van een nummer o Decimaal systeemcijfer hangt af van de positie die het inneemt wanneer het deel uitmaakt van een figuur. Daarom wordt gezegd dat het een positionele waarde is. Een heel eenvoudig voorbeeld: de Relatieve waarde van 1 In nummer 123, Het wordt 100, Omdat ik de positie van de honderden inneemt.

Een ander voorbeeld: Nummer 58 wordt gevormd door cijfers 5 en 8. Door deze figuur van rechts naar links te onderzoeken, is de relatieve waarde van 8 8, omdat het in de positie van de eenheden is en de relatieve waarde van 5 is 50, voor het bezetten van de locatie van de tientallen. Het nummer wordt gelezen "Fifty -Eight".

Aan de andere kant hebben dezelfde cijfers verschillende relatieve waarden in nummer 85, omdat ze posities hebben uitgewisseld. Altijd beginnend van rechts naar links, is de relatieve waarde van 5 in dit geval 5, de relatieve waarde van 8 is 80 en het nummer wordt gelezen "Tachtig -Five".

Hoe u de relatieve waarde van een nummer kunt vinden?

De algemene procedure om de relatieve waarde van elk cijfer te vinden is als volgt:

• Het eerste cijfer van rechts naar links is in de positie van de eenheden en hun waarde wordt vermenigvuldigd met 1.
• Het volgende cijfer komt overeen met de tientallen en wordt vermenigvuldigd met 10.
• De volgende positie komt overeen met de honderden en de waarde van het cijfer wordt vermenigvuldigd met 100.
• De volgende positie is duizend, daarom wordt het cijfer vermenigvuldigd met 1000.

Enzovoort voor grotere aantallen, het cijfer vermenigvuldigen met het overeenkomstige 10 vermogen: 100000, 100000 en verder.

Nummer 321 kan bijvoorbeeld worden geschreven als 3*100 + 2*10 + 1*1, of gelijkwaardig 300 + 20 + 1. In het vorige voorbeeld is snel te zien dat de relatieve waarde van 3 300 is, 2 is 20 en 1 is 1.

Kan u van dienst zijn: distributieve eigendom

Voorbeelden van relatieve waarden

Nummer 727

Om de relatieve waarde van een cijfer te bepalen, moet u worden geleid door het volgende basisprincipe van de schriftelijke nummering van het decimale systeem:

Elk cijfer links van een ander vertegenwoordigt een eenheid 10 keer hoger, en vice versa: Elk cijfer rechts van een ander vertegenwoordigt een eenheid 10 keer kleiner. 

Het 727 -figuur, dat "zevenhonderd twintig -seven" leest, bestaat bijvoorbeeld uit cijfers 2 en 7, met 7 herhaalde, maar verschillende posities innemen.

Lezen 727 van rechts naar links, wordt opgemerkt dat de 7 rechts de positie van de eenheid inneemt, daarom wordt deze vermenigvuldigd met 1:

7 x 1 = 7

En de relatieve waarde ervan is 7.

Digit 2 in het midden neemt de positie van de tientallen in en om hun relatieve waarde te vinden, wordt deze vermenigvuldigd met 10:

2 x 10 = 20

Eindelijk op de 7 naar het uiterste links heeft de positie van de honderden. Dan moet je zich met 100 vermenigvuldigen en de relatieve waarde ervan is:

7 x 100 = 700

Merk op dat alleen wanneer het cijfer de positie van de eenheid inneemt, is dat zijn absolute waarde en de relatieve waarde gelijk zijn. Daarom, als de relatieve waarde van het nummer VR is en de absolute waarde ervan VA is, is de algemene formule om de relatieve waarde te vinden:

VR = absolute waarde Va × waarde van zijn positie

Een figuur kan worden geschreven als de som van de relatieve waarden van zijn cijfers, dit staat bekend als ontwikkelde notatie. Doorgaan met het voorbeeld van nummer 727 moet u:

727 = 700 + 20 + 7

En als u liever de bevoegdheden van 10 gebruikt, wordt het getal 727 ook uitgedrukt als:

727 = 7 ∙ 10² + 2 ∙ 10¹ + 7 ∙ 10⁰

Het kan u van dienst zijn: veelvouden van 8: wat zijn en uitleg

Waarbij de exponenten van het vermogen op basis van 10 de positie van elk cijfer vertegenwoordigen en worden genoemd Indices. In de volgende figuur wordt een ander voorbeeld geïllustreerd.

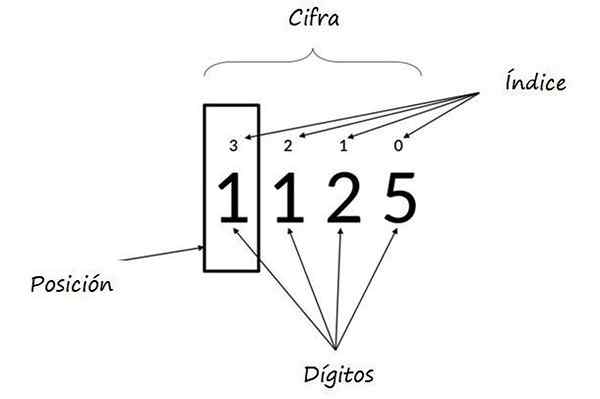In getal 1125 is de relatieve waarde van 5 5, de 2 is 20, de 1 is 100 en de linker 1 in de doos is 1000. Bron: Wikimedia Commons.

Nummer 63

Beginnend van links naar rechts, bevindt de 3 zich daarom in de positie van de eenheden:

Relatieve waarde van 3: 3 x 1 = 3

Wat betreft 6, dit is in de positie van de tientallen, dan:

Relatieve waarde van 6: 6 x 10 = 60

Nummer 603

Deze figuur verschilt van de vorige, want hoewel de relatieve waarde van 0 0 is, hebben de andere cijfers verschillende relatieve waarden. Beginnend van rechts naar links zoals altijd:

• Relatieve waarde van 3: 3 x 1 = 3
• Relatieve waarde van 0: 0 x 10 = 0
• Relatieve waarde van 6: 6 x 100 = 600

Nummer 630

In dit geval is 0 in de positie van de eenheden:

• Relatieve waarde van 0: 0 x 1 = 0
• Relatieve waarde van 3: 3 x 10 = 30
• Relatieve waarde van 6: 6 x 100 = 600

Opgeloste oefeningen

Oefening 1

Geef de relatieve waarde van de onderstreepte getallen aan:

a) 1209

b) 2782

c) 376

d) 3045

e) 273

Oplossing

a) cijfer 1 op 1209 neemt de positie in van de duizend of duizenden. Daarom is de relatieve waarde ervan 1000.

VR (1) = 1 x 1000 = 1000

b) De 2 bezet de positie van de eenheden in 2782, daarom is de relatieve waarde ervan 2.

c) In 376 bevindt de 7 zich in de positie van de tientallen en::

VR (7) = 7 x 10 = 70.

d) In 3045 bevindt de 4 zich ook in de positie van de tientallen:

VR (4) = 4 x 10 = 40.

e) tegen 273 is de 3 in de plaats van de eenheden en hun relatieve waarde valt samen met de figuur van het cijfer, dat wil zeggen:

Kan je van dienst zijn: zeshoekige piramide

VR (3) = 3 x 1 = 3

Oefening 2

Schrijf het laagste aantal van 5 cijfers, zonder enige wordt herhaald en voldoet aan de volgende voorwaarden:

a) dat alle cijfers anders zijn

b) Het heeft een 7 in de duizend

c) De 8 bevindt zich in de positie van de eenheden.

Oplossing voor

Het kleinste nummer van 5 -cijfer, met allemaal, moet met allemaal beginnen met 1, omdat hoewel 0 lager is, omdat het eerste cijfer links niet telt, daarom is het gezochte nummer:

10234

Oplossing B

De Millar -positie voor 7 komt overeen met 7000, maar omdat u de kleinst mogelijke figuur wilt die 5 cijfers bevat, moet het nummer beginnen met 1, gevolgd door 7 en vervolgens 023 in de resterende posities, omdat er geen cijfer moet worden herhaald.

Daarom is het nummer:

17023

Oplossing C

Zoals gevraagd dat de 8 in de positie van de eenheden zijn, moet dit rechtsonder zijn. Als het minst mogelijke nummer, zonder dat een van de 5 cijfers wordt herhaald, is het gezochte nummer:

10238

Oefening 3

Bereken de absolute en relatieve waarde (van elke figuur) van het nummer 579.

Oplossing

Het heeft dat 579 gelijk is aan 5 × 100+7 × 10+9 × 1, of gelijkwaardig, het is gelijk aan 500+70+9. Daarom is de relatieve waarde van 5 500, de relatieve waarde van 7 is 70 en de 9 is 9.

Aan de andere kant is de absolute waarde van 579 gelijk aan 579.

Oefening 4

Geef het nummer 9.648.736, wat is de relatieve waarde van 9 en eerste 6 (van links naar rechts)? Wat is de absolute waarde van het gegeven nummer?

Oplossing

Door te herschrijven naar nummer 9.648.736 wordt verkregen dat dit gelijk is aan

9 × 1.000.000 + 6 × 100.000 + 4 × 10.000 + 8 × 1.000 + 7 × 100 + 3 × 10 + 6 × 1

Of je kunt schrijven zoals

9.000.000 + 600.000 + 40.000 + 8.000 + 700 + 30 + 6.

Zodat de relatieve waarde van 9 9 is.000.000 en de relatieve waarde van de eerste 6 is 600.000.

Aan de andere kant is de absolute waarde van het gegeven nummer 9.648.736.