Ovale (geometrische figuur) kenmerken, voorbeelden, oefeningen

Hij ovaal Symmetric wordt gedefinieerd als een vlakke en gesloten curve, die twee loodrechte symmetrie -assen heeft - één major en een minderjarige - en bestaat uit twee cirkelbogen gelijk aan twee tot twee tot twee tot twee tot twee tot twee tot twee tot twee tot twee.

Op deze manier kunt u tekenen met behulp van een kompas en enkele referentiepunten op een van de symmetrie -assen. In elk geval zijn er verschillende manieren om het te tekenen, zoals we later zullen zien.

Figuur 1. View van het Colosseum van Rome, een voorbeeld van een ovale vorm in de architectuur. Bron: Pixabay.

Het is een zeer bekende curve, omdat het wordt herkend als de contour van een ellips, dit is een bepaald geval van het ovaal. Maar het ovaal is geen ellips, hoewel het soms veel lijkt, omdat de eigenschappen en getraceerde verschillen verschillen. De ellips is bijvoorbeeld niet gebouwd met kompas.

[TOC]

Kenmerken

The Oval heeft zeer gevarieerde toepassingen: architectuur, industrie, grafisch ontwerp, horlogemaking en sieraden zijn slechts enkele gebieden waar het gebruik ervan opvalt.

De meest opvallende kenmerken van deze belangrijke curve zijn de volgende:

-Het behoort tot de groep technische curven: het wordt getraceerd om omtrekbogen te vormen met behulp van een kompas.

-Al zijn punten zijn op hetzelfde vliegtuig.

-Het mist curven of banden.

-De lay -out is continu.

-De ovale curve moet zacht en convex zijn.

-Wanneer u een raaklijn naar het ovaal trekt, staat alles aan dezelfde kant van de lijn.

-Een ovaal ondersteunt twee raaklijnen parallel aan de meeste.

Voorbeelden

Er zijn verschillende methoden om ovalen te bouwen die het gebruik van regel, ploeg en kompas vereisen. Dan zullen we enkele van de meest gebruikte vermelden.

Kan u van dienst zijn: ongelijkheid van de driehoek: demonstratie, voorbeelden, opgeloste oefeningen

Constructie van een ovaal door concentrische omtrek

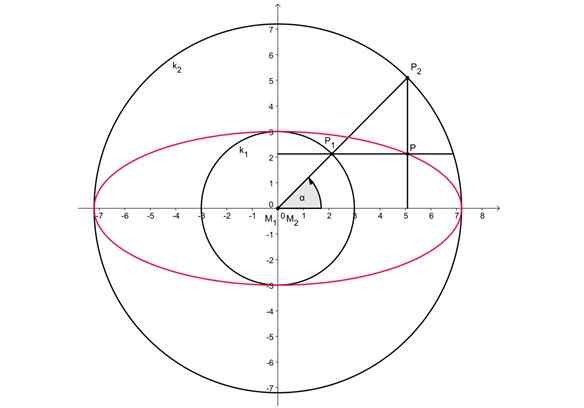Figuur 2. Manier om een ​​ovaal te trekken door twee concentrische omtrek. Bron: Wikimedia Commons. Kmhkmh [cc door 3.0 (https: // creativeCommons.Org/licenties/door/3.0)]

Figuur 2 hierboven toont twee concentrische omtrek met het midden van de oorsprong. De belangrijkste ovale as meet hetzelfde als de diameter van de externe omtrek, terwijl de kleinere as overeenkomt met de diameter van de binnenomtrek.

-Een willekeurige straal wordt aangetrokken door de buitenomtrek, die beide omtrek in de P -punten snijdt₁ En P₂.

-Dan wordt punt P geprojecteerd₂ Op de horizontale as.

-Op dezelfde manier wordt punt P geprojecteerd₁ op de verticale as.

-De kruising van beide projectielijnen is punt P en behoort tot het ovaal.

-Alle punten in dit gedeelte van het ovaal kunnen op deze manier worden getekend.

-De rest van het ovaal wordt getekend met de analoge procedure, uitgevoerd in elk kwadrant.

Opdrachten

Dan worden andere manieren om ovalen te bouwen, worden onderzocht, gegeven een bepaalde initiële maatregel, die de grootte ervan zal bepalen.

- Oefening 1

Teken met een regel en kompas een ovaal, bekend zijn belangrijkste as waarvan de lengte 9 cm is.

Oplossing

In figuur 3, die hieronder wordt getoond, verschijnt het resulterende ovaal in rood. Speciale aandacht moet worden besteed aan de stippellijnen, die de hulpconstructies zijn die nodig zijn om een ​​ovaal te tekenen waarvan de belangrijkste as is gespecificeerd. We zullen alle nodige stappen aangeven om de uiteindelijke tekening te bereiken.

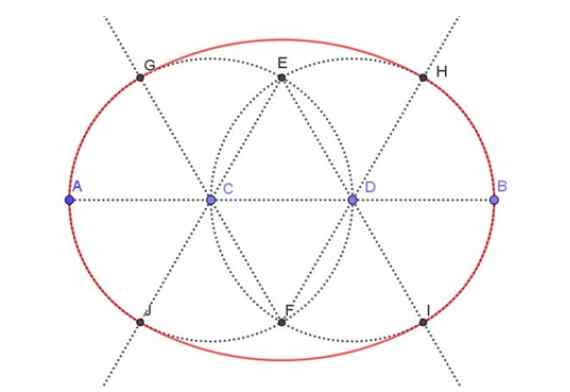figuur 3. Constructie van een ovaal gezien de belangrijkste as. Bron: f. Zapata.

Stap 1

Teken het AB -segment van 9 cm met een regel.

Kan u van dienst zijn: Bayes Stelling

Stap 2

Het AB -segment opdrijven, dat wil zeggen het delen in drie segmenten van gelijke lengte. Aangezien het oorspronkelijke AB -segment 9 cm meet, moeten de AC-, CD- en DB -segmenten elk 3 cm meten.

Stap 3

Met het kompas trekt het openen van C en CA een hulpomtrek. Evenzo wordt de hulpomtrek van centrum D en radio -DB getekend met het kompas.

Stap 4

De kruispunten van de twee hulpomtrek die in de vorige stap zijn gebouwd, zijn gemarkeerd. We noemen het punten e en f.

Stap 5

Met de regel de volgende semi -recreas.

Stap 6

De semi -strak van de vorige stap sneed naar de twee hulpomtrek op respectievelijk punten G, H, I, J.

Stap 7

Met het kompas wordt het in f en met opening (of radio) fg de boog getekend Gh. Evenzo is het maken van centrum op e en met radio -ei de boog getekend IJ.

Stap 8

De vereniging van de bogen GJ, Ji, IH En Hg Ze vormen een ovaal waarvan de belangrijkste as 9 cm meet.

Stap 9

De hulppunten en beroertes worden gewist (Hide).

- Oefening 2

Teken met regel en kompas een ovaal, waarvan de kleine as bekend is en de maatregel is 6 cm.

Oplossing

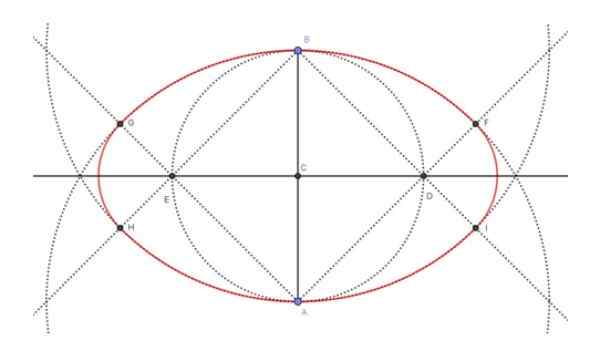Figuur 4. Constructie van een ovaal gezien zijn kleine as. Bron: f. Zapata.

De bovenstaande figuur (figuur 4) toont het eindresultaat van de constructie van het ovaal (in rood), evenals de tussenliggende constructies die nodig zijn om het te bereiken. De stappen die werden gevolgd om de kleine as ovaal 6 cm te bouwen, waren de volgende:

Stap 1

De 6 cm lange segment AB wordt getekend met de regel.

Kan u van dienst zijn: theorie instellen: kenmerken, elementen, voorbeelden, oefeningen

Stap 2

Met het kompas en de regel wordt de MediaTrix aangetrokken door het AB -segment.

Stap 3

De kruising van de MediaTrix met het AB -segment resulteert in het middelpunt C van het AB -segment.

Stap 4

Met het kompas is de omtrek van Centro C en Radio CA getekend.

Stap 5

De omtrek in de vorige stap onderschept de MediaTrix van AB op punten E en D.

Stap 6

De semi -rechtse [advertentie), [ae), [bd) en [be) zijn getekend.

Stap 7

Met het kompas zijn de Center A en Radio AB en de Centro B en Radio BA Radio B en Radio BA getekend.

Stap 8

De kruispunten van de omtrek getrokken in stap 7, met de semi -straight gebouwd in stap 6, bepalen vier punten, namelijk: f, g, h, i.

Stap 9

Met het centrum in d en radio di de boog als hij wordt getekend. Op dezelfde manier is de GH -boog met E en Radio bijv.

Stap 10

De vereniging van de omtrekbogen FG, GH, HI en als het gezochte ovaal bepalen.

Referenties

1. Plastic ed. Technische krommen: ovale, eivormige en spiralen. Hersteld van: Draw.WordPress.com.
2. Mathematische Basteleien. Eiercurven en ovalen. Opgehaald uit: Mathematische-Basteleien.
3. Universiteit van Valencia. Conische en platte technische curven. Hersteld van: ocw.UV.is.
4. Wikipedia. ovaal. Hersteld van: is.Wikipedia.borg.
5. Wikipedia. ovaal. Opgehaald uit: in.Wikipedia.borg.