Diameter symbolen en formules, hoe het uit te schakelen, omtrek

Hij diameter Het is de rechte lijn die door het midden van een gesloten vlakke curve of een figuur in twee of drie dimensies gaat en die ook bij zijn tegenovergestelde punten komt. Het is meestal een cirkel (een platte curve), een cirkel (een platte figuur), een bol of een rechte cirkelvormige cilinder (drie -dimensionale objecten).

Hoewel de omtrek en de cirkel meestal als synoniemen worden beschouwd, is er een verschil tussen beide termen. De omtrek is de gesloten curve die omsluit in de cirkel, die voldoet aan de voorwaarde dat de afstand tussen een van zijn punten en het midden hetzelfde is. Deze afstand is niemand minder dan de straal van de omtrek. In plaats daarvan is de cirkel een platte figuur beperkt door de omtrek.

Figuur 1. De diameter van de fietswielen is een belangrijk kenmerk in het ontwerp. Bron: Pixabay.

In het geval van omtrek, cirkel en bol is de diameter een recht segment dat ten minste drie punten bevat: het midden plus twee punten van de rand van de omtrek of cirkel, of het oppervlak van de bol.

En wat betreft de rechte cirkelvormige cilinder, de diameter verwijst naar de dwarsdoorsnede, die samen met de hoogte zijn twee karakteristieke parameters zijn.

De diameter van de omtrek en de cirkel, gesymboliseerd door Ø of gewoon de letter "D" of "D", is gerelateerd aan de perimeter, contour of lengte, die wordt aangeduid met de letter L:

L = π.D = π. of

Wanneer u een omtrek heeft, is het quotiënt tussen de lengte en de diameter van de irrationele getal π = 3.14159 ..., op deze manier:

π = L/D

[TOC]

Hoe u de diameter kunt krijgen?

Wanneer de tekening van de omtrek of cirkel beschikbaar is, of direct het cirkelvormige object, zoals een valuta of een ring, is het heel gemakkelijk om de diameter met een regel te nemen. U moet er gewoon voor zorgen dat de rand van de regel tegelijkertijd twee punten van de omtrek en het centrum van hetzelfde heeft.

Kan u van dienst zijn: algebraic

Een kaliber, Vernier of King's Foot is zeer geschikt voor het meten van externe en interne diameters in munten, hoepels, ringen, noten, buizen en meer.

Figuur 2. Vernier digitale meten van de diameter van een munt. Bron: Pixabay.

In plaats van het object of de tekening hebben u gegevens zoals de radio R, Dan vermenigvuldigen met 2, je hebt de diameter. En als de lengte of omtrek van de omtrek bekend is, kan de diameter ook bekend zijn, door klaring:

D = 2.R
D = l / π

Een andere manier om de diameter te krijgen, is om het cirkelgebied, het bolvormige oppervlak, de dwarsdoorsnede van de cilinder, het gebogen oppervlak van deze of de volumes van de bol of de cilinder te kennen. Het hangt allemaal af van welke geometrische figuur het is. De diameter is bijvoorbeeld betrokken bij de volgende gebieden en volumes:

-Cirkelgebied: π.(D/2)²
-Sferisch oppervlak: 4π.(D/2)²
-Bolvolume: (4/3) π.(D/2)³
-Rechte cirkelvormige cilindervolume: π.(D/2)².H (H is de cilinderhoogte)

Figuren van constante breed

De cirkel is een platte figuur van constante breed, want waar het ook uitziet, de breedte is diameter d. Er zijn echter andere misschien minder bekende figuren waarvan de breedte ook constant is.

Laten we eerst kijken wat wordt begrepen door de breedte van een figuur: het is de afstand tussen twee parallelle lijnen -support remes -die op zijn beurt loodrecht op de gegeven richting staan ​​en die de figuur opsluiten, zoals weergegeven in de linker afbeelding:

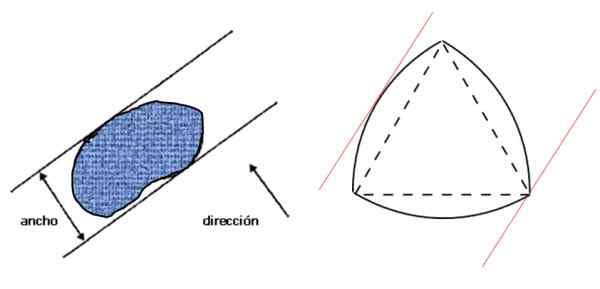figuur 3. Breedte van elke platte figuur (links) en Reuleaux -driehoek, een constante brede figuur (rechts). Bron: f. Zapata.

Rechts rechts is de Reuleaux -driehoek, die een constante brede figuur is en die voldoet aan de in de linker figuur gespecificeerde toestand. Als de breedte van de figuur D is, wordt de omtrek ervan gegeven door de stelling van Barbier:

Kan u van dienst zijn: bij benadering meting van amorfe figuren: voorbeeld en oefening

L = π.D

De riolen van de stad San Francisco in Californië hebben de vorm van Reuleaux's Triangle, genoemd door de Duitse ingenieur Franz Reuleaux (1829 - 1905). Op deze manier kan de tapas niet langs het gat vallen en minder materiaal uitgeven om ze te produceren, omdat hun gebied minder is dan dat van de cirkel:

A = (1- √3).πD² = 0.705.D²

Terwijl voor een cirkel:

A = π.(D/2)² = (π/4) D²= 0.785.D²

Maar deze driehoek is niet de enige constante brede figuur. Oproepen kunnen worden gebouwd Reuleaux polygonen met andere polygonen die een vreemde zijkanten hebben.

Diameter van een omtrek

In de volgende figuur zijn de elementen van de omtrek, als volgt gedefinieerd:

Touw: lijnsegment dat twee punten van de omtrek verbindt. In de figuur staat het touw dat zich bij de punten C en D verbindt, maar oneindige snaren kunnen worden getraceerd die uniek is van een paar punten van de omtrek.

Diameter: Het is het touw dat door het centrum gaat en twee punten van de omtrek verbindt met het midden of. Het is het langste touw van een omtrek, om die reden wordt het "major touw" genoemd.

Radio: lijnsegment dat met elk punt van de omtrek het midden bij het midden voegt. De waarde ervan, net als de diameter, is constant.

Omtrek: Het is de set van alle punten die gelijk zijn of.

Boog: Het wordt gedefinieerd als een omtreksegment gescheiden door twee radio's (niet getekend in de figuur).

Figuur 4. Delen van de omtrek, inclusief de diameter, die door het midden passeren. Bron: Wikimedia Commons.

- voorbeeld 1

De getoonde rechthoek meet 10 inch lang, die bij het wikkelen een rechte cirkelvormige cilinder vormt waarvan de diameter 5 inch is. Beantwoord de volgende vragen:

Het kan u van dienst zijn: wederzijds exclusieve gebeurtenissen: eigenschappen en voorbeelden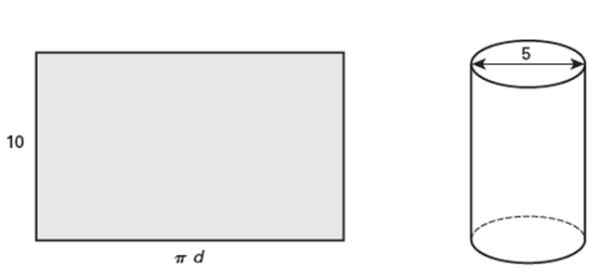Figuur 5. Een opgerolde rechthoek wordt een rechte cirkelvormige cilinder. Bron: Jiménez, r. Wiskunde II. Geometrie en trigonometrie. 2e. Editie. Pearson.

a) Wat is de contour van de buis?
b) Zoek het rechthoekige gebied
c) Bereken het kruis -sectiegebied van de cilinder.

Oplossing voor

De contour van de buis is l = π.D = 5π PLG = 15.71 PLG.

Oplossing B

Het rechthoekige gebied is Basis X Hoogte, De basis zijn al al berekend en de hoogte is 10 PLG volgens de verklaring, daarom:

A = 15.71 PLG x 10 PLG = 157.1 PLG².

Oplossing C

Ten slotte wordt het gevraagde gebied als volgt berekend:

A = π.(D/2)² = (π/4) D² = (π/4) x (5 PLG)²= 19.63 PLG².

- Voorbeeld 2

Bereken het gearceerde gebied van figuur 5A. Het plein heeft zij L.

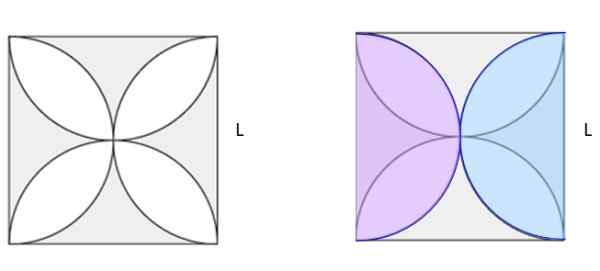Figuur 6. Vind het gearceerde gebied in de linker figuur. Jiménez, r. Wiskunde II. Geometrie en trigonometrie. 2e. Editie. Pearson.

Oplossing

In figuur 5b zijn twee identieke semicirkels van grootte in roze en blauwe kleuren getekend, gesuperponeerd op de originele figuur. Tussen hen maken ze een complete cirkel. Als het vierkant van het vierkant wordt berekend en het cirkelgebied wordt afgetrokken, maakt het het gearceerde gebied van figuur 5b. En er goed uitziet, het blijkt dat het de helft van het schaduwrijke gebied is in 5A.

-Area Square: L²
-Semi -cirkel diameter: l
-Cirkelgebied: π.(L/2)²= (π/4) l²
-Verschil van gebieden = de helft van het gearceerde gebied =

L² - (π/4) l² = [(4 - π)/4] l²= 0.2146 L²

-Gearceerd gebied = 2 x 0.2146 L²= 0.4292L2

Hoeveel diameters heeft een omtrek?

Oneindige diameters kunnen in een cirkel worden getekend, en elk van hen meet hetzelfde.

Referenties

1. Antonio. Reuleaux -driehoeken en andere constante breedtecurves. Hersteld van: verspreiding.com.
2. Baldor, een. 2002. Flat and Space and Trigonometry Geometry. Culturele thuislandgroep.
3. Jiménez, r. Wiskunde II. Geometrie en trigonometrie. 2e. Editie. Pearson.
4. Wikipedia. Reuleaux -driehoek. Hersteld van: het is.Wikipedia.borg.
5. Wolfram Mathworld. Diameter. Hersteld van: Mathworld.Wolfraam.com.