Perfect vierkant trinomiaal

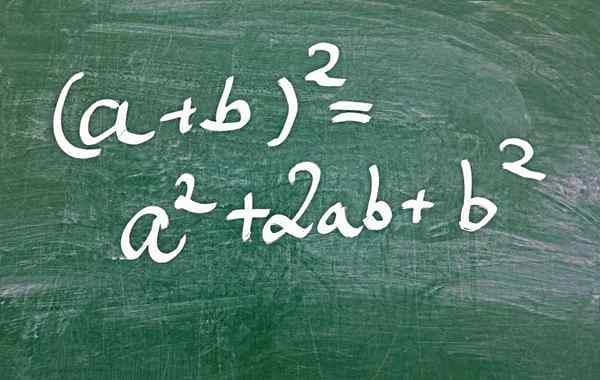Figuur 1.- Een van de manieren om een ​​perfect vierkant trinomiaal te verkrijgen is door het kwadraat van de som

Wat is het perfecte vierkante trinomiaal?

Het perfecte vierkante trinomiale is dat polynoom van drie termen, waarvan er twee perfecte vierkanten zijn van de hoeveelheden A en B en worden voorafgegaan door hetzelfde teken, terwijl de derde term precies het dubbele product van A en B is, een ander teken.

Een perfect vierkant trinomiaal wordt verkregen door vierkant

naar² ± 2 ∙ AB + B²

Zoals te zien is, bevat de perfecte vierkante trinomiale:

• Twee niet -vergelijkbare kwadratische termen voorafgegaan door hetzelfde teken: a² en B²
• Een derde term 2 ∙ AB, het dubbele product van de vierkante wortels van de kwadratische termen en die kan worden voorafgegaan door een positief of negatief teken.

Perfecte vierkante trinomials kunnen een of meer variabel zijn. Het volgende trinomiaal is bijvoorbeeld een perfect vierkant van een variabele:

• X² + 6x + 9

Merk op dat de eerste termen (x²) en derde (9) zijn respectievelijk vierkant van de bedragen die A en B worden genoemd. Inderdaad, x² Het is het vierkant van X en 9 is het vierkant van 3. Op deze manier kunt u het volgende schrijven:

A = x

B = 3

En de resterende term is het dubbele product van X en 3:

6x = 2 ∙ 3 ​​∙ x

Zodra de verificatie is gemaakt, is het zeker dat dit trinomiaal perfect vierkant is.

Voorbeelden

Figuur 2.- Voorbeelden van perfecte vierkante trinomen. Bron: f. Zapata.

Perfecte vierkante trinomials verschijnen ook in twee of meer variabelen, bijvoorbeeld:

4x² + 4xy + en²

Het is een trinomiaal in twee variabelen: "X" en "Y". Het kan er zeker van zijn dat het een perfect vierkante trinomiaal is, omdat het twee kwadratische termen presenteert:

4x² = (2x)²

En² = (y)²

En de resterende term is het dubbele product van de respectieve vierkante wortels: "2x" en "y":

Kan u van dienst zijn: orthoedro: formules, gebied, volume, diagonaal, voorbeelden

4xy = 2 ∙ 2x ∙ en

De tot nu toe gepresenteerde trinomen zijn graad 2 in de variabele "x", maar ze hoeven niet noodzakelijk zo te zijn. Het volgende trinomiaal is graad 4 in "X":

9x⁴ - 30x²YZ + 25y²Z²

Het is gemakkelijk te verifiëren dat dit een perfect vierkante trinomiaal is. De eerste term is het perfecte 3x vierkant², Sinds (3x²))² = 9x⁴.

De term 25y²Z² is gelijk aan (5yz)². Ten slotte is de resterende term 2 ∙ 3x²∙ 5YZ = 30 x²en z.

Aan de andere kant zijn de hieronder getoonde trinomials geen perfecte vierkante trinomials:

• X²  + 8x - 16

Het is geen perfect vierkant trinomiaal omdat 16, hoewel het 4 is², Het wordt voorafgegaan door een negatief teken, terwijl de andere kwadratische term (x²) is positief.

• X²  - 15x + 25

Het is ook niet een perfect vierkante trinomiaal, want hoewel het twee kwadratische termen heeft: x² en 5², De term 15x is niet gelijk aan 2 ∙ 5 ∙ x.

• 4x²  + 10x + 32

Dit trinomiaal is niet perfect vierkant, omdat het alleen een kwadratische term bevat: 4x² = (2x)².

Vierkant van een som en vierkant van een verschil

Perfecte vierkante trinomials worden verkregen door twee soorten opmerkelijke producten te ontwikkelen:

• Het vierkant van de som.
• Het vierkant van het verschil.

Eerst wordt de ontwikkeling verkregen van de distributieve eigenschap, omdat het verhogen van de vierkante binomiale middelen het met zichzelf vermenigvuldigen:

(A ± B)² = (a ± b) × (a ± b) = a² ± A ∙ B ± B ∙ A + B² = A² ± 2A ∙ B + B²

De verkregen trinomiale is een resultaat dat wordt onthouden met slechts een beetje oefening en een soort snelkoppeling is die de ontwikkeling vergemakkelijkt, daarom wordt het een opmerkelijk product genoemd.

Kan u van dienst zijn: transcendente nummers: wat zijn, formules, voorbeelden, oefeningen

De volgende trinomials worden gemakkelijk verkregen door een opmerkelijk product, zonder de eigenschappen van distributie opnieuw aan te passen.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5y + 2x)² = (5y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 en² +20xy + 4x²

Factorisatie van een perfect vierkant trinomiaal

Een frequente en noodzakelijke werking in algebra is de factorisatie van het perfecte vierkante trinomiaal, waardoor het trinomiaal wordt uitgedrukt als het kwadraat van een som of een aftrekking van twee termen (een binomiaal).

Het is de omgekeerde bewerking om het opmerkelijke product te ontwikkelen, omdat het idee heeft om het resulterende trinomiaal te hebben, het idee om de binomiale te verkrijgen die ertoe leidt wanneer het opkomt tot de 2.

Bijvoorbeeld in de eerder geanalyseerde 4x Perfect Square Trinomial² + 4xy + en², Wat is het binomiale dat wanneer het vierkant is, het aanleiding geeft tot jou?

De respectieve vierkante wortels van de kwadratische termen zijn:

√ (4x²) = 2x

Dat is gelijk aan: 4x² = (2x)²

√ (en²) = y

Gelijk aan dat te zeggen: en² = (y)²

Daarom:

4x² + 4xy + en² = (2x + y)²

En wat is het binomiale dat de perfecte vierkante trinomiale 9x is⁴ - 30x²YZ + 25y²Z²? Opnieuw worden de vierkante wortels van de kwadratische termen geëxtraheerd:

√ (9x⁴) = 3x²

√ (25 en²Z²) = 5YZ

Dus:

(3x² - 5yz)² = 9x⁴ - 30x²YZ + 25y²Z²

Opgeloste oefeningen

Oefening 1

Voltooi in elk van de volgende trinomials de blanco met de term die ontbreekt om een ​​perfect vierkant trinomiaal te zijn:

ben² + 18m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Oplossing voor

Volgens de formule van het opmerkelijke product:

Kan u van dienst zijn: complementaire hoeken: welke en hoe ze worden berekend, voorbeelden, oefeningen

(A ± B)² = A² ± 2A ∙ B + B²

Van het trinomiale:

M² + 18m + _____

Het volgt dat:

a = m (zodat² = m²))

Bovendien is de centrale term: 2 ∙ a ∙ b = 2m ∙ b = 18m, daarom b = 9 en het vierkant is 9² = 81. Guy door de formule van het opmerkelijke product, het trinomiaal is zo:

(M + 9)² = M² + 18m + 81

• Oplossing B

In dit trinomiaal:

4x² - _____ + 64

Je kunt het weten en b:

A = √ (4x²) = 2x

B = √64 = 8

Daarom is de ontbrekende term het dubbele product van A en B:

2 ∙ AB = 2 ∙ 8 ∙ 2x = 32x

En de gezochte trinomiale is:

4x² - 32x + 64

• Oplossing C

In het trinomiale:

_____ + 30n + 25

De eerste term ontbreekt, maar het is bekend dat:

B = √25 = 5

EN

2 ∙ AB = 2 ∙ A ∙ 5 = 10a = 30n

Daarom is a = 3n en de gezochte trinomiaal:

9n² + 30n + 25

Oefening 2

Controleer of het volgende een perfect vierkant trinomiaal is en factor is:

16y² - 24yz + 9z²

• Oplossing

Eerst is bewezen dat de kwadratische termen worden voorafgegaan door hetzelfde teken en vervolgens worden de respectieve vierkante wortels gevonden:

A = √ (16y²) = 4y

B = √ (9Z²) = 3Z

Dan moet u verifiëren of de resterende term het dubbele product van A en B is:

2 ∙ AB = 2 ∙ 4y ∙ 3Z = 24YZ

Als dat zo is, kan de trinomiale factor zijn als het kwadraat van een verschil, omdat de centrale term wordt voorafgegaan door een negatief teken:

16y² - 24yz + 9z² = (4y - 3z)²

Referenties

1. Jiménez, r. 2008. Algebra. Prentice Hall.
2. Kate's wiskundelessen. Perfecte vierkante trinomials. Hersteld van: Katesmathlessons.com.
3. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
4. Zill, D. 2008. Voorrang op berekening vooruitgang. 4e. Editie. McGraw Hill.