Balacket Triangle -kenmerken, eigenschappen, formules, gebied

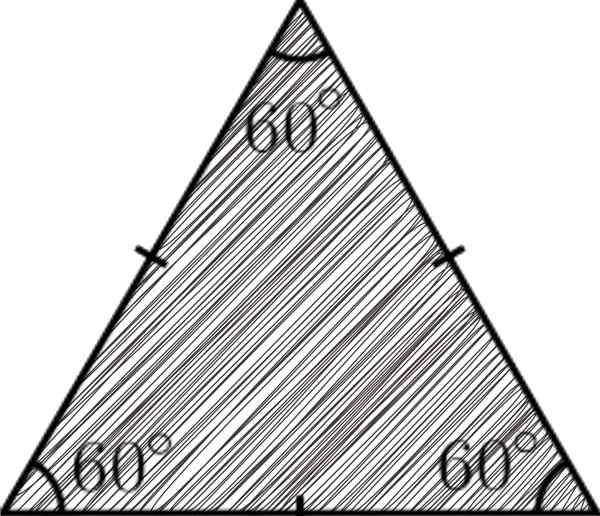
A gelijkzijdige driehoek Het is een driezijdige polygoon, waar iedereen hetzelfde is; dat wil zeggen, ze hebben dezelfde maatregel. Voor dat kenmerk kreeg het de naam van gelijkzijdige (gelijke kanten).

De driehoeken zijn polygonen beschouwd als de eenvoudigste in geometrie, omdat drie zijden, drie hoeken en drie hoekpunten worden gevormd. In het geval van de gelijkzijdige driehoek, voor het hebben van gelijke kanten, impliceert dit dat de drie hoeken ook zullen zijn.

Een voorbeeld van de gelijkzijdige driehoek

[TOC]

Kenmerken van de evenwichtsdriehoeken

- Gelijke kanten

De gelijkzijdige driehoeken zijn platte en gesloten cijfers, samengesteld uit drie lijnen met lijnen. De driehoeken worden geclassificeerd door hun kenmerken, in relatie tot hun zijden en hoeken; Het gelijkzijdige werd geclassificeerd met behulp van de maat van hun zijkanten als een parameter, omdat deze exact hetzelfde zijn, dat wil zeggen dat ze congruent zijn.

De gelijkzijdige driehoek is een bepaald geval van de gelijkbenige driehoek omdat twee van zijn zijden congruent zijn. Dat is de reden waarom alle gelijkzijdige driehoeken ook gelijkbenig zijn, maar niet alle gelijkbenige driehoeken zullen gelijkwaardig zijn.

Op deze manier hebben de gelijkzijdige driehoeken dezelfde eigenschappen van een gelijkbenige driehoek.

De gelijkzijdige driehoeken kunnen ook worden geclassificeerd door de amplitude van hun interne hoeken als een gelijkzijdige acute driehoek, die alle drie de zijden en drie interne hoeken met dezelfde maat heeft. De hoeken zullen acuut zijn, dat wil zeggen, ze zullen minder zijn dan 90^of.

- Componenten

Driehoeken hebben in het algemeen verschillende regels en punten die het samenstellen. Ze worden gebruikt om het gebied, zijden, hoeken, mediaan, bissector, mediatrix en hoogte te berekenen.

• De mediaan: Het is een lijn die van het middelpunt aan één kant vertrekt en het tegenovergestelde hoekpunt bereikt. De drie mediums aanwezig op een punt genaamd Baricentro of Centroid.
• De bissector: Het is een semi -rechterk die de hoek van de hoekpunten in twee hoeken van gelijke mate verdeelt, dus het staat bekend als symmetrieasas. De gelijkzijdige driehoek heeft drie assen van symmetrie. In de gelijkzijdige driehoek wordt de bissector uit het hoekpunt van een hoek naar de tegenovergestelde zijde getrokken, waardoor het in zijn middelpunt snijdt. Je bent op de naam InCenter.
• De MediaTrix: Het is een segment dat een voorbeeld van de zijkant van de driehoek is die in het midden hiervan is ontstaan. Er zijn drie mediatica in een driehoek en ze zijn het eens op een punt genaamd Circumcentro.
• De hoogte: Het is de lijn die van het hoekpunt gaat naar de zijde die tegengesteld is en deze lijn ook loodrecht op die kant staat. Alle driehoeken hebben drie hoogten die samenvallen op een punt dat Ortotenter wordt genoemd.

In de volgende grafiek observeren we een scaleense driehoek waar sommige van de bovengenoemde componenten gedetailleerd zijn

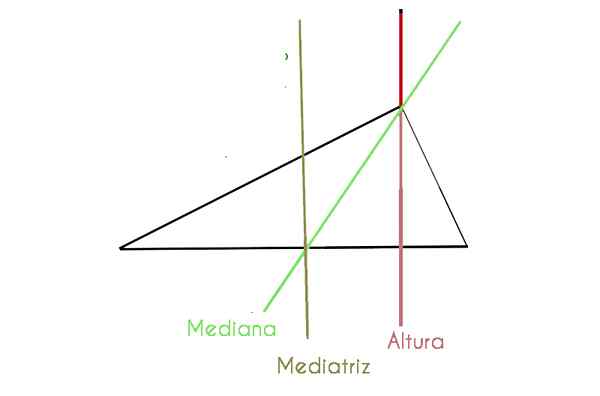We kunnen duidelijk de componenten zien, iets dat moeilijker is in de gelijkzijdige driehoek, omdat sommigen samenvallen. We leggen ze hieronder uit:

De bissector, de mediaan en mediatrix zijn toevallig

De bissector verdeelt zich naast een driehoek in twee delen. In gelijkzijdige driehoeken zal die kant worden verdeeld in twee exact dezelfde delen, dat wil zeggen dat de driehoek zal worden verdeeld in twee congruente rechthoeken driehoeken.

Aldus valt de bissector uit elke hoek van een gelijkzijdige driehoek samen met de mediaan en de mediatrix aan de andere kant van die hoek.

Kan u van dienst zijn: evenredigheidsrelaties: concept, voorbeelden en oefeningen

Voorbeeld:

De volgende figuur toont de ABC -driehoek met een midden D die een van zijn zijden verdeelt in twee AD- en BD -segmenten.

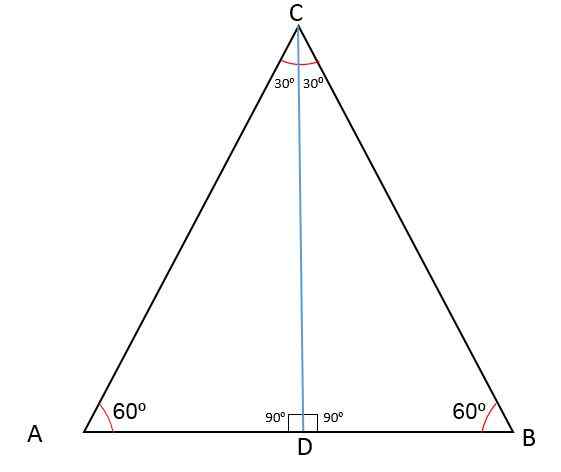
Bij het trekken van een lijn van punt D naar het tegenovergestelde hoekpunt, wordt per definitie de mediane CD verkregen, die relatief is ten opzichte van hoekpunt C en tot de zijde AB.

Terwijl het CD -segment de ABC -driehoek verdeelt in twee gelijke CDB- en CDA -driehoeken, betekent dit dat het het geval zal zijn van congruentie: kant, hoek, kant en daarom zal CD ook de BCD -bissector zijn.

Bij het tekenen van het CD -segment is de hoekpunthoek verdeeld in twee gelijke hoeken van 30^of, De hoek van het hoekpunt A blijft 60 meten^of En de CD -lijn vormt een hoek van 90^of Met betrekking tot het middelpunt D.

Het CD -segment vormt hoeken die dezelfde maatregel hebben voor ADC- en BDC -driehoeken, dat wil zeggen dat ze zo aanvullend zijn dat de maat van elk zal zijn:

Med. (ADB) + Med. (ADC) = 180^of

2 _* Med. (ADC) = 180^of

Med. (ADC) = 180^of ÷ 2

Med. (ADC) = 90^of.

En dus is het CD -segment ook de MediaTrix aan de AB -kant.

De bissector en hoogte zijn toevallig

Wanneer de bissector vanaf het hoekpunt van een hoek naar het middelpunt van de andere kant volgt, verdeelt dit de gelijkzijdige driehoek in twee congruente driehoeken.

Op zo'n manier dat een hoek van 90 wordt gevormd^of (direct). Dit geeft aan dat dit lijnsegment volledig loodrecht op die kant staat, en per definitie zou die lijn de hoogte zijn.

Op deze manier valt de bissector van elke hoek van een gelijkzijdige driehoek samen met de hoogte ten opzichte van de andere kant van die hoek.

Orocentro, Baricentro, Incentro en Colecentro munten

Aangezien de hoogte, mediaan, bissector en mediatrix tegelijkertijd door hetzelfde segment worden weergegeven, in een gelijkzijdige driehoek de ontmoetingspunten van deze segmenten -de orthocenter, baricenter, st incenter en besnijdenis -zullen op hetzelfde punt worden gevonden:

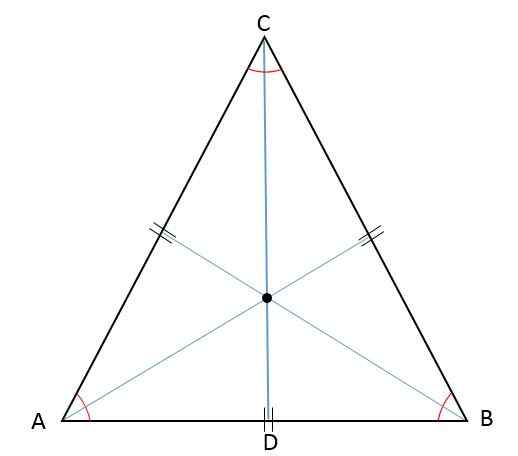
Eigenschappen

Het belangrijkste eigendom van de gelijkzijdige driehoeken is dat het altijd gelijkbenige driehoeken zullen zijn, omdat de gelijkbenige worden gevormd door twee congruente partijen en de evenwicht door drie.

Op deze manier erfden de gelijkzijdige driehoeken alle eigenschappen van de gelijkbenige driehoek:

Interne hoeken

De som van interne hoeken is altijd gelijk aan 180^of, En omdat al zijn hoeken congruent zijn, zal elk van deze 60 meten^of.

Externe hoeken

De som van externe hoeken zal altijd gelijk zijn aan 360^of, Daarom zal elke externe hoek 120 meten^of. Dat komt omdat interne en externe hoeken aanvullend zijn, dat wil zeggen, door ze toe te voegen, zullen ze altijd gelijk zijn aan 180^of.

Som van de zijkanten

De som van de metingen van twee zijden moet altijd groter zijn dan de maat van de derde zijde, dat wil zeggen a + b> c, waarbij a, b en c de metingen aan elke kant zijn.

Congruente partijen

De gelijkzijdige driehoeken hebben hun drie zijden met dezelfde maat of lengte; dat wil zeggen, ze zijn congruent. Daarom moet je in het vorige item = B = C.

Congruente hoeken

De gelijkzijdige driehoeken staan ​​ook bekend als EqangeGulous Triangles, omdat hun drie interne hoeken met elkaar congruent zijn. Dit komt omdat al hun partijen ook dezelfde maatregel hebben.

Het kan u van dienst zijn: nominale variabele: concept en voorbeelden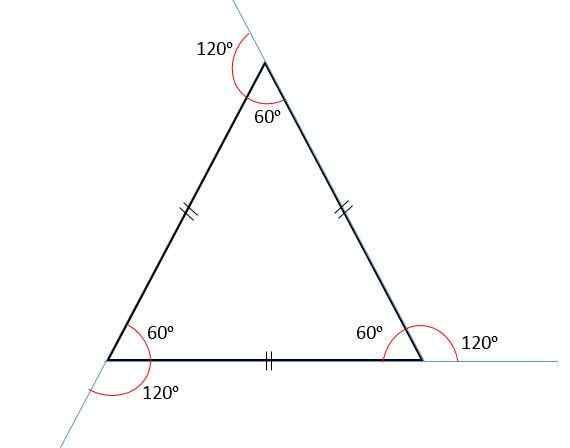

Hoe de omtrek te berekenen?

De omtrek van een polygoon wordt berekend door de som van de zijkanten. Zoals in dit geval heeft de gelijkzijdige driehoek al zijn zijden met dezelfde maatregel, wordt de omtrek ervan berekend met de volgende formule:

P = 3 _* kant.

Hoe de hoogte te berekenen?

Aangezien de hoogte de lijn loodrecht op de basis is, verdeelt u deze in twee gelijke delen door zich uit te breiden naar het tegenovergestelde hoekpunt. Aldus worden twee driehoeken gelijke rechthoeken gevormd.

De hoogte (H) vertegenwoordigt de tegenovergestelde cateto (A), de helft van de AC -zijde van de aangrenzende cateto (B) en de BC -zijde vertegenwoordigt de hypotenuse (C).

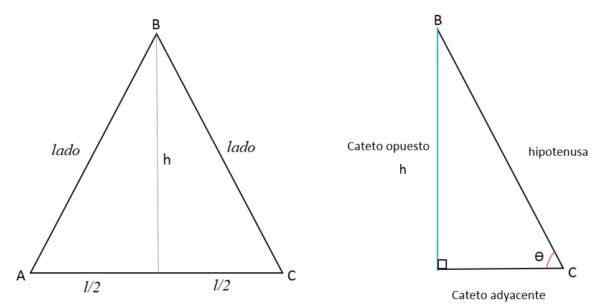
Met behulp van de Pythagoras -stelling kan de waarde van de hoogte worden bepaald:

naar² + B² = c²

Waar:

naar² = hoogte (h).

B² = zijde b / 2.

C² = zijde a.

Die waarden vervangen in de stelling van Pythagoras en het wissen van de hoogte die je hebt:

H² + (( l / 2)² = l²

H² +  l²/ 4 = l²

H² = l²  -  l²/ 4

H² = (4_*l² -  l²)) / 4

H² =  3_*l² /4

√H² = √ (3_*l² /4)

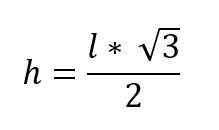
Als de hoek gevormd door de congruente zijden, de hoogte (vertegenwoordigd door een been) bekend is, kan deze worden berekend door de trigonometrische redenen toe te passen.

De categorieën worden tegenovergestelde of aangrenzend genoemd, afhankelijk van de hoek die als referentie wordt genomen.

In de vorige figuur is de cateto h bijvoorbeeld tegengesteld voor hoek C, maar naast hoek B:

De hoogte kan dus worden berekend met:

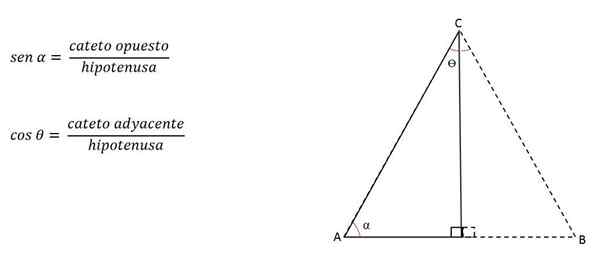
Hoe de zijkanten te berekenen?

Er zijn gevallen waarin de maatregelen van de driehoekszijden niet bekend zijn, maar de hoogte en de hoeken die in de hoekpunten worden gevormd.

Om het gebied in deze gevallen te bepalen, is het noodzakelijk om trigonometrische redenen toe te passen.

Als je de hoek van een van zijn hoekpunten kent, wordt de categorie geïdentificeerd en wordt de overeenkomstige trigonometrische reden gebruikt:

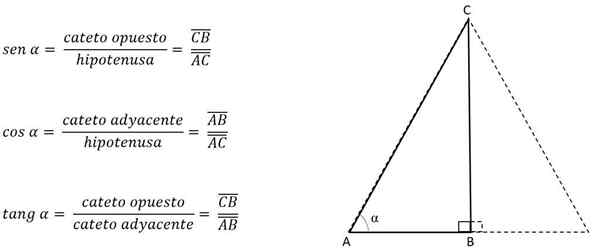
Aldus zal de cateto AB tegen hoek C zijn, maar naast de hoek a. Afhankelijk van de zijkant of been die overeenkomt met de hoogte, wordt de andere kant gewist om de waarde hiervan te verkrijgen, wetende dat in een gelijkzijdige driehoek de drie zijden altijd dezelfde maat hebben.

Hoe het gebied te berekenen?

De driehoeken worden altijd berekend met dezelfde formule, waardoor de basis wordt vermenigvuldigd met hoogte en door twee delen:

Gebied = (b _* H) ÷ 2

Wetende dat de hoogte wordt gegeven door de formule:

Opdrachten

- Eerste oefening

De zijkanten van een ABC -gelijkzijdige driehoek meet elk 20 cm. Bereken de hoogte en het oppervlak van die polygoon.

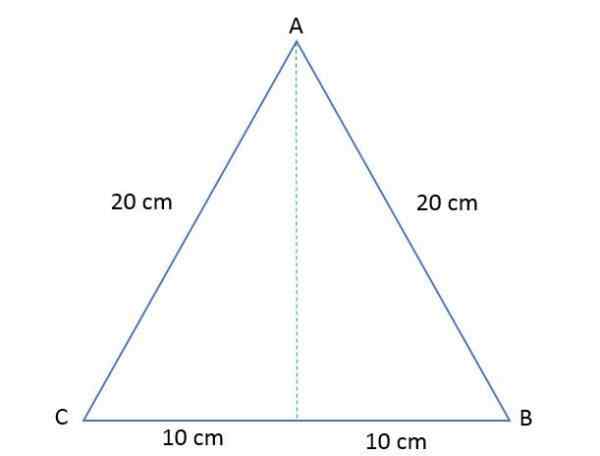
Oplossing

Om het gebied van die gelijkzijdige driehoek te bepalen, is het noodzakelijk om de hoogte te berekenen, wetende dat het bij het trekken ervan de driehoek verdeelt in twee gelijke rechthoeken.

Op die manier kunt u Pythagoras -stelling gebruiken om het te vinden:

naar² + B² = c²

Waar:

A = 20/2 = 10 cm.

B = hoogte.

C = 20 cm.

De gegevens worden vervangen in de stelling:

10² + B² = 20²

100 cm + B² = 400 cm

B² = (400 - 100) cm

B² = 300 cm

B = √300 cm

B = 17,32 cm.

Dat wil zeggen, de hoogte van de driehoek is gelijk aan 17,32 cm. Nu is het mogelijk om het gegeven driehoekgebied te berekenen door de formule te vervangen:

Gebied = (b _* H) ÷ 2

Gebied = (20 cm _* 17.32 cm) ÷ 2

Het kan u van dienst zijn: lineaire transformaties: eigenschappen, wat zijn het gebruik, typen, voorbeelden

Gebied = 346,40 cm² ÷ 2

Gebied = 173,20 cm².

Een andere eenvoudigere manier om de oefening op te lossen, is het vervangen van de gegevens in de directe formule van het gebied, waar de waarde van de hoogte ook impliciet wordt gevonden:

- Tweede oefening

In een veld met de vorm van een gelijkzijdige driehoek, zullen bloemen planten. Als de omtrek van dat terrein gelijk is aan 450 m, bereken dan het aantal meters dat de bloemen bezet.

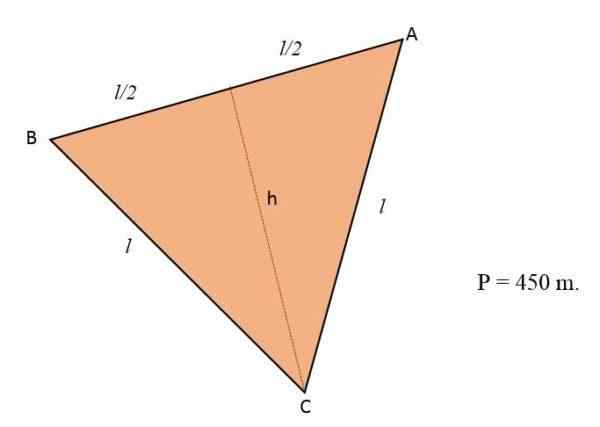
Oplossing

Wetende dat de omtrek van een driehoek overeenkomt met de som van zijn drie zijden en omdat het terrein de vorm heeft van een gelijkzijdige driehoek, hebben de drie zijden hiervan dezelfde maat of lengte:

P = zijde + zijde + zijde = 3 _* l

3 _* l = 450 m.

L = 450 m ÷ 3

L = 150 m.

Nu is het alleen nodig om de hoogte van die driehoek te berekenen.

De hoogte verdeelt de driehoek in twee congruente rechthoeken driehoeken, waar een van de categorieën de hoogte en de andere helft van de basis vertegenwoordigt. Door de stelling van Pythagoras kan de hoogte worden bepaald:

naar² + B² = c²

Waar:

naar = 150 m ÷ 2 = 75 m.

C = 150 m.

B = hoogte

De gegevens worden vervangen in de stelling:

(75 m)² + B² = (150 m)²

5.625 m + B² = 22.500 m

B² = 22.500 m - 5.625 m

B² = 16.875 m

B = √16.875 m

B = 129,90 m.

Het gebied dat bloemen zullen bezetten, zal dus zijn:

Gebied = B * H ÷ 2

Gebied = (150 m _* 129,9 m) ÷ 2

Gebied = (19.485 m²) ÷ 2

Gebied = 9.742.5 m²

- Derde oefening

De ABC -gelijkzijdige driehoek wordt gedeeld door een lijnsegment dat van zijn hoekpunt C naar het middelpunt d gaat, gelegen aan de andere kant (AB). Dit segment meet 62 meter. Bereken het gebied en de omtrek van die gelijkzijdige driehoek.

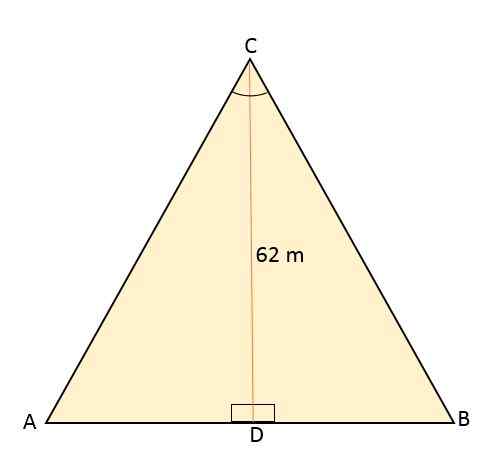
Oplossing

Wetende dat de gelijkzijdige driehoek wordt gedeeld door een lijnsegment dat overeenkomt met de hoogte, waardoor twee congruente rechthoeken worden gevormd, verdeelt dit op zijn beurt ook de hoek van hoekpunt C in twee hoeken met dezelfde maatregel, 30^of elk.

De hoogte vormt een hoek van 90^of Met betrekking tot segment AB en de hoek van het hoekpunt om vervolgens 60 te meten^of.

Gebruik vervolgens de hoek van 30 als referentie^of, CD -hoogte wordt vastgesteld als een cateto grenzend aan de hoek en BC als hypotenusa.

Uit deze gegevens kan de waarde van een van de zijden van de driehoek worden bepaald, met behulp van de trigonometrische redenen:

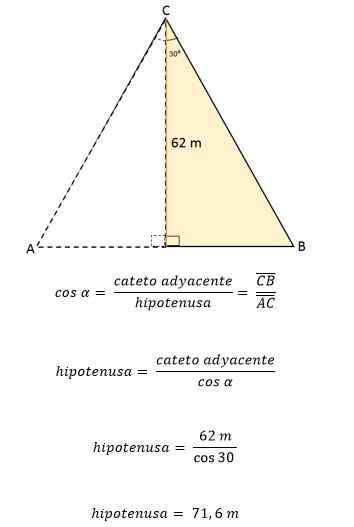
Zoals in de gelijkzijdige driehoek alle zijden hebben exact dezelfde maat of lengte, betekent dit dat elke zijde van de ABC -gelijkzijdige driehoek gelijk is aan 71,6 meter. Wetende dat het mogelijk is om uw gebied te bepalen:

Gebied = B * H ÷ 2

Gebied = (71,6 m _* 62 m) ÷ 2

Gebied = 4.438,6 m² ÷ 2

Gebied = 2.219.3 m²

De omtrek wordt gegeven door de som van zijn drie zijden:

P = zijde + zijde + zijde = 3 _* l

P = 3_*l

P = 3 _* 71,6 m

P = 214,8 m.

Referenties

1. Álvaro Rendón,. R. (2004). Technische tekening: activiteiten notebook.
2. Arthur Goodman, L. H. ( 1996). Algebra en trigonometrie met analytische geometrie. Pearson Education.
3. Baldor, een. (1941). Algebra. Havana: Cultuur.
4. Barbosa, J. L. (2006). Vlakke Euclidische geometrie. SBM. Rio de Janeiro, .
5. Coxford, een. (1971). Geometrie Een transformatiebenadering. VS: Laidlaw Brothers.
6. Euclid, r. P. (1886). Euclid's elementen van geometrie.
7. Héctor Trejo, J. S. (2006). Geometrie en trigonometrie.
8. León Fernández, G. S. (2007). Geïntegreerde geometrie. Grootstedelijk technologisch instituut.
9. Sullivan, J. (2006). Algebra en trigonometrie. Pearson Education.