TESELADOS -kenmerken, typen (regelmatig, onregelmatig), voorbeelden

De Mozeer Het zijn oppervlakken die worden bedekt door een of meer cijfers genoemd Tessel. Ze zijn overal: in alle soorten straten en gebouwen. Tessels of tegels zijn platte stukken, meestal polygonen met congruente of isometrische kopieën, die volgens een normaal patroon worden geplaatst. Op deze manier zijn er geen spaties zonder te worden bedekt en overlappen de tegels of mozaïeken niet. 

In het geval dat een enkel type mozaïek gevormd door een gewone polygoon wordt gebruikt, is er een Regelmatig Teseld, Maar als twee of meer soorten reguliere polygonen worden gebruikt, dan is het een Semi -regelmatig tede moraad.

Figuur 1. Onregelmatige tegelvloervloer, omdat rechthoeken niet-reguliere polygonen zijn, zelfs als de vierkanten dat zijn. Bron: Pixabay.

Ten slotte wanneer de polygonen die de Tesseldo vormen niet regelmatig zijn, dus het is een onregelmatige tessel.

Het meest voorkomende type Tesseldo is dat gevormd door rechthoekige en bijzonder vierkante mozaïeken. In figuur 1 hebben we een goed voorbeeld.

[TOC]

Geschiedenis van de Teselados

Tessellatie wordt al duizenden jaren gebruikt om vloeren en muren van paleizen en tempels van verschillende culturen en religies te bedekken.

Bijvoorbeeld de Sumerische beschaving die rond 3500 bloeide.C. Ten zuiden van Mesopotamië, tussen de Eufraat en Tigris -rivieren, gebruikten ze de Tesels in hun architectuur.

Figuur 2. Teselados Sumerios aan de deur van Istar. Bron: Wikimedia Commons.

De Tesels hebben ook de interesse gewekt van de wiskundigen aller tijden: beginnend met Archimedes in de derde eeuw voor Christus, gevolgd door Johannes Kepler in 1619, Camille Jordan in 1880, tot hedendaagse tijden met Roger Penrose.

Het kan u van dienst zijn: fractie gelijk aan 3/5 (oplossing en uitleg)

Penrose creëerde een niet -periodieke tessellatie die bekend staat als Penrose -mozeling. ENdeze Het zijn slechts enkele namen van wetenschappers die veel hebben bijgedragen over tessellatie.

Regelmatige Tesels

Regelmatige wegverlaa worden gemaakt met een enkel type gewone polygoon. Aan de andere kant, zodat de Teseldo kan worden beschouwd als regelmatig alle punt van het vliegtuig moet:

-Behoren tot het interieur van het polygoon

-Of aan de rand van twee aangrenzende polygonen 

-Ten slotte kan het behoren tot het gemeenschappelijke hoekpunt van ten minste drie polygonen.

Met de bovenstaande beperkingen kan worden aangetoond dat alleen de gelijkzijdige driehoeken, de vierkanten en de zeshoeken een normaal tes kunnen vormen.

Nomenclatuur

Er is een nomenclatuur om de Tesels aan te duiden die bestaat uit vermelding in de richting van de kloknaalden en gescheiden door een punt, het aantal zijden van de polygonen die elk knooppunt (of hoekpunt) van de mozeel omringen, altijd beginnend met het kleinste aantal van zijkanten.

Deze nomenclatuur is van toepassing op reguliere en semi -regelmatige Tesselves. 

Voorbeeld 1: driehoekige Teselado

Figuur 3 toont een driehoekige gewone tegel. Opgemerkt moet worden dat elk driehoekige tegelknoop het gemeenschappelijke hoekpunt is van zes gelijkzijdige driehoeken. 

De manier om dit type Tesseldo aan te geven is 3.3.3.3.3.3, die ook wordt aangegeven door 3⁶.

figuur 3. Driehoekige reguliere Teselado 3.3.3.3.3.3. Bron: Wikimedia Commons

Voorbeeld 2: Square Tessel

Figuur 4 toont een reguliere tegel die alleen uit vierkanten bestaat. Opgemerkt moet worden dat elk tegelknooppunt is omgeven door vier congruente vierkanten. De notatie die van toepassing is op dit type vierkante tesselves is: 4.4.4.4 o afwisselend 4⁴

Figuur 4. Vierkante Teseld 4.4.4.4. Bron: Wikimedia Commons.

Voorbeeld 3: Hexagonal Teseld

In een zeshoekige Tesselle. De nomenclatuur voor een regulier hexagonaal tede mozeel is 6.6.6 o afwisselend 6³.

Kan u van dienst zijn: conische secties: typen, toepassingen, voorbeelden Figuur 5. Zeshoekige Teseld 6.6.6. Bron: Wikimedia Commons.

Semi -regelmatig tede moraad

Semi -regelmatige of getelbare Tesels van Archimedes bestaat uit twee of meer soorten reguliere polygonen. Elk knooppunt wordt omgeven door de soorten polygonen die de moza in dezelfde volgorde vormen en de toestand van een rand die volledig wordt gedeeld met de buurman wordt gehandhaafd.

Er zijn acht semi -regelmatige Tesels:

1. 3.6.3.6 (Tri-hexagonal tesselled)
2. 3.3.3.3.6 (hexagonal teslate romo)
3. 3.3.3.4.4 (Elongado driehoekige Teselado)
4. 3.3.4.3.4 (Romo Square ToSelled)
5. 3.4.6.4 (Rombi-tri-hexagonal Teseld)
6. 4.8.8 (afgeknot vierkant tede mozeel)
7. 3.12.12 (afgeknotte zeshoekige Teseld)
8. 4.6.12 (afgeknotte tri-hexagonal Teseld)

Enkele voorbeelden van semi -reguliere teslate worden hieronder weergegeven.

Voorbeeld 4: Tixagonal Teselado

Het is degene die bestaat uit reguliere gelijkzijdige driehoeken in structuur 3.6.3.6, wat betekent dat een tegelknooppunt is omgeven (totdat het een terugkeer voltooit) door een driehoek, een zeshoek, een driehoek en een zeshoek. Figuur 6 toont zo'n tessel.

Figuur 6. Tri-hexagonal Teseld (3.6.3.6) Het is een voorbeeld van semi -reguliere tessel. Bron: Wikimedia Commons.

Voorbeeld 5: Hexagonal Teseldo Romo

Net als de tegel van het vorige voorbeeld, bestaat dit ook uit driehoeken en zeshoeken, maar de verdeling ervan rond een knooppunt is 3.3.3.3.6. Figuur 7 illustreert duidelijk dit type tesselled.

Figuur 7. De zeshoekige Tesseldo Romo bestaat uit een zeshoek omringd door 16 driehoeken in configuratie 3.3.3.3.6. Bron: Wikimedia Commons.

Voorbeeld 6: Rombi-tri-hexagonal Tessel

Het is een tegel die bestaat uit driehoeken, vierkanten en zeshoeken, in configuratie 3.4.6.4, dat wordt getoond in figuur 8.

Figuur 8. Semi -reguliere moorsnede samengesteld uit een driehoek, een vierkant en een zeshoek in configuratie 3.4.6.4. Bron: Wikimedia Commons.

Onregelmatige Tesels

Ze worden onregelmatige Tesels genoemd voor die die worden gevormd door onregelmatige polygonen, of door reguliere polygonen, maar die niet voldoen aan het criterium dat een knooppunt een hoekpunt is van ten minste drie polygonen.

Het kan u van dienst zijn: antiderivatief: formules en vergelijkingen, voorbeelden, oefeningen

Voorbeeld 7

Figuur 9 toont een voorbeeld van onregelmatige tegels, waarin alle polygonen regelmatig en congruent zijn. Het is onregelmatig omdat een knooppunt geen gemeenschappelijk hoekpunt is van ten minste drie vierkanten en er zijn ook aangrenzende vierkanten die geen voorsprong delen.

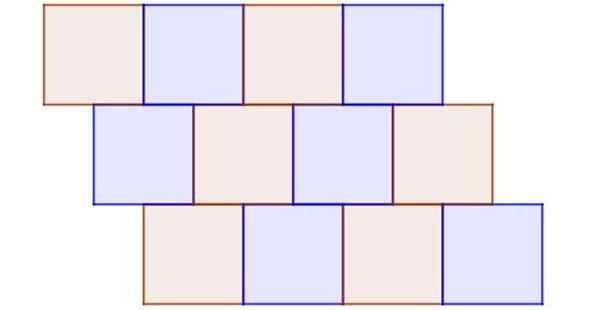Figuur 9. Zelfs als alle tegels congruente vierkanten zijn, is dit een duidelijk voorbeeld van onregelmatige tessel. Bron: f. Zapata.

Voorbeeld 8

Het parallellogram is een plat oppervlak, maar tenzij het een vierkant is, kan het geen normaal teen zijn.

Figuur 10. Een Teseldo gevormd door parallellogrammen is onregelmatig, omdat de mozaïeken niet -reguliere polygonen zijn. Bron: f. Zapata.

Voorbeeld 9

Niet-reguliere zeshoeken met centrale symmetrie hebben een plat oppervlak ingesteld, zoals getoond in de volgende figuur:

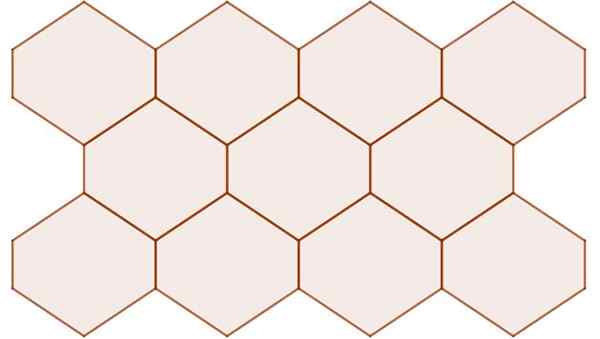Figuur 11. Zeshoeken met centrale symmetrie, zelfs als ze niet regelmatig zijn, zetten ze het vliegtuig in. Bron: f. Zapata.

Voorbeeld 10: El Cairo Teselado

Het is een zeer interessante moza, samengesteld uit pentagons met zijkanten van gikke lengte maar met ongelijke hoeken, waarvan er twee recht zijn en de andere drie elk 120º hebben.

Zijn naam komt dat deze Tesseld in de stoep is van sommige straten van Caïro in Egypte. Figuur 12 toont de Tesseldo van Caïro.

Figuur 12. Caïro Tesseldo. Bron: Wikimedia Commons.

Voorbeeld 11: Teselado al-Andalus

Tesseldo wordt tijdens sommige delen van Andalusië en Noord -Afrika gekenmerkt door geometrie en epigrafie, naast sierelementen zoals vegetatie. 

Palacios 'getostelde zoals de Alhambra samengesteld uit tegels gevormd door keramische stukken van vele kleuren, met meerdere (niet te zeggen oneindige) vormen die geometrische plots hebben geactiveerd.

Figuur 13. Teselado Palacio de la Alhambra. Tartaglia / Public Domain

Voorbeeld 12: Teselado in de videogees

Ook bekend als TESELLATION, het is een van de meest boom in videogames. Dit is het creëren van texturen om de Teseld van de verschillende scenario's die in de simulator verschijnen te simuleren.

Dit is de duidelijke reflectie dat deze hoes blijven evolueren door de grenzen van de werkelijkheid over te dragen.

Referenties

1. Geniet van wiskunde. Tesels. Hersteld van: geniet van Matimaticas.com
2. Rubiños. Tesels loste voorbeelden op. Hersteld van: wiskunde.Blogspot.com
3. Weisstein, Eric W. "Deiregula tessellation". Weisstein, Eric W, ED. Wiskunde. Wolfram -onderzoek.
4. Wikipedia. Mozeer. Hersteld van: is.Wikipedia.com
5. Wikipedia. Regelmatig Teseld. Hersteld van: is.Wikipedia.com