Tidecágono

Figuur 1.- Links een reguliere Tridecácágone en rechts een valuta van 20 kronen van de Tsjechische Republiek, met een Bridecagon -vormige contour ingeschreven in een omtrek, enerzijds heeft het de leeuw van Bohemen en ander aan San WenceLao, Patron van de Tsjechische Republiek, te paard gemonteerd. Bron: f. Zapata.

Wat is een tridecágono?

Tridecagon is een platte geometrische figuur van de Polygons -familie en die worden gekenmerkt door 13 zijden en 13 hoekpunten. Een andere naam voor deze polygoon is Triskaidecágono, Nummer afgeleid van Grieks.

De 13 zijkanten zijn lijnsegmenten die uiteindelijk dichtbij de figuur zijn gevormd. De polygonen, die volgens de hoeveelheid zijden worden genoemd, zijn een rijke bron van inspiratie voor de architectuur, constructie en het ontwerp van talloze objecten, zowel kunst als utilitariërs.

Eigenschappen van Tridecágono

De Tridecágono deelt met de andere polygonen de volgende kenmerken en eigenschappen:

-Zijkanten, Het zijn de lijnsegmenten die zijn verbonden om de figuur te vormen, die in het geval van de Tridecágono 13 zijn. Ze worden geïdentificeerd door kleine letters.

-Hoekpunten, Dit is wat de snijpunten van opeenvolgende zijden worden genoemd en meestal aangeven met hoofdletters. De Tridecágono heeft 13 hoekpunten.

-Omtrek, gelijkwaardig aan de som van de zijkanten. Als alle zijden gelijke maatregel "a" hebben, is de perimeter gewoon 13 × a, maar als de zijkanten ongelijk zijn, voegt de omtrek elk van de lengtes van de zijkanten toe.

-Centrum, Het is het punt dat dezelfde afstand bijhoudt met zowel de hoekpunten als de zijkanten.

-Diagonaal, Een lijn die een hoekpunt vergezelt aan een ander niet -opeenvolgend hoekpunt (de opeenvolgende hoekpunten zijn verenigd door de partijen).

-Interne hoeken, Ze worden gevormd tussen twee aangrenzende zijden van de figuur en op het binnenste deel van de polygoon, en het hoekpunt is het gemeenschappelijke hoekpunt voor beide kanten.

Kan u van dienst zijn: miletus Een dergelijke stelling

-Externe hoeken, Ze zijn buiten de polygoon, tussen één kant en de verlenging van een van de opeenvolgende zijden naar de eerste.

-Radio, Afstandafstand-vertix van de Tridecágon.

-Centrale hoek, Het is degene wiens hoekpunt het midden van de polygoon is.

-Apothem, segment dat samenwerkt aan het midden van één zijde met het midden van de figuur en vormt 90º met die kant.

Gewone en onregelmatige donder

ThreeCarons kunnen zijn:

-Normaal, Wanneer de maat van al zijn dertien zijden hetzelfde is en zijn interne hoeken hetzelfde meten.

-Onregelmatig, Als een of meer van de zijden verschillende maatregelen hebben.

In het geval van de reguliere Tridecácágone kunnen de volgende formules worden toegepast:

Interne hoek

Voor een normale polygoon is de formule waarmee de waarde van de interne hoek kan worden berekend:

Waarbij n het aantal zijden vertegenwoordigt, dat in dit geval 13 is. Met deze waarde is het:

I = (11 × 180º)/13 ≈ 152.3e

Diagonalen

Het aantal diagonalen wordt berekend door de volgende formule, zelfs geldig als de polygoon onregelmatig is:

Voor n = 13 resultaten:

D = 13 × 10/2 = 65 diagonalen

Apothem

De waarde van apothem l_NAAR  Het wordt berekend met de volgende formule, "A" de lengte van de zijde:

L_NAAR ≅ 2.0286A

Gebied

Als de omtrek P en de lengte van de apothem l_NAAR, Het Tridecágono -gebied wordt berekend door:

A = (P × L_NAAR)/2

Afhankelijk van de "A" -zijde blijft de formule:

A = (13a × l_NAAR)/2

De maatregel vervangen_NAAR Uit de vorige sectie wordt een formule voor het gebied dat alleen afhankelijk is van de lengte van de zijde verkregen:

A = (13a × 2.0286a)/2 ≈ 13.186a²

Kan u van dienst zijn: Hypergeometrische verdeling: formules, vergelijkingen, model

Oefening

Als de diameter van een kronen van 20 mm 26 mm is, hoeveel zijn de zijkant en het gebied van de Tridecágono geregistreerd in de cirkel van de valuta?

Oplossing

Uit de figuur is er een rechthoekige driehoek, waarvan de categorieën de apothem zijn en de helft van de lengte van de zijkant, met de hypotenusa gelijk aan de straal van de valuta, die de helft van de diameter is. Omdat dit 26 mm waard is, is Radio R gelijk aan 13 mm.

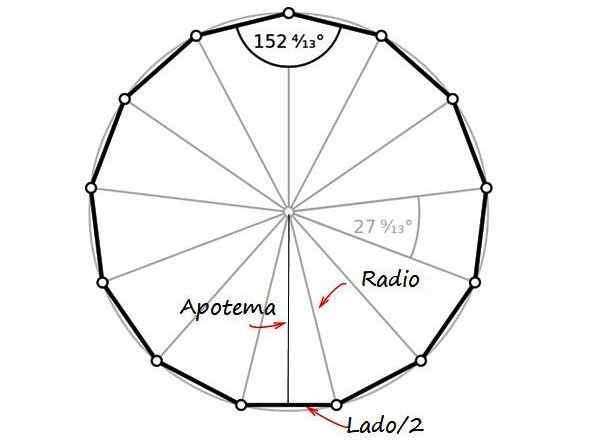Figuur 2. De radio, het apotheme en de helft van de zijkant van de trindecagon vormen een rechthoekige driehoek. Bron: Wikimedia Commons/F. Zapata.

Door Pythagoras Stelling:

Sinds L_NAAR ≈ 2.0286a, je hebt:

R² = (2.0286a)² + (0.5e)² = 4.3652a²

De zijkant is:

Met deze waarde is het gebied van de valuta:

A ≈ 13.186a² = 13.186 (6.222 mm)² = 510.5 mm²

De lezer wordt achtergelaten om dit resultaat te vergelijken met het verkregen gebied door aan te nemen dat de valuta circulair is met straal r = 13 mm.

Hoe is een tridecágono?

De reguliere trindecagon is van de polygonen die geen exacte constructie toelaat met alleen regel en kompas, dat wil zeggen dat het geen bouwbare polygoon is. Ze zijn alleen maar gebouwd, althans in theorie, die polygonen waarvan het aantal zijden alleen belangrijke factoren van de vorm omvat:

De priemgetallen worden op die manier genoemd Fermat Cousins, Maar het nummer 13, hoewel het neef is, heeft deze vorm niet.

U kunt echter een normale trindecagon tekenen die in een omtrek is geregistreerd, elk hoekpunt heeft een kruising ermee, zonder in het blote oog te worden opgemerkt. Hiervoor is het nodig.

Kan u van dienst zijn: Obsusangle Triangle

Een manier om een ​​reguliere Tridecácágone te bouwen, hoewel niet de enige, is de beroertes trekken zoals getoond in de volgende animatie:

figuur 3. Constructie van een gewone trideCagon. Bron: Wikimedia Commons.

En deze andere animatie beschrijft ook hoe je ongeveer een Tridecágono kunt maken, met regel en kompas:

Figuur 4.- Alternatieve manier om een ​​ongeveer regelmatige tridecagon te bouwen met regel en kompas. Bron: Wikimedia Commons.

Voorbeelden van Tridecágel

Concave en convex donder

Wanneer de interne hoeken van de Tridecágono minder zijn dan 180º, is de figuur convex, terwijl als een of meer interne hoeken groter zijn dan 180º, de Tridecágono concaaf is.

De reguliere Tridecácágon is convex, omdat de interne hoeken ongeveer 152 meten.3e elk.

Gebruik van tridecágono in numismatiek

Tsjechische kroon

Numismaticics is de wetenschap van munten, medailles, tickets en chips. De polygonen aan vele kanten zijn ideaal als decoratieve elementen in het ontwerp van munten, vooral die met veel kanten, zoals de Tridecágono.

Niet alle munten zijn rond, maar de polygonen aan veel kanten lijken op de cirkelvormige vorm, hoe meer kanten het heeft, hoe groter de nadering. Daarom gebruiken muntenontwerpers de polygonen aan vele partijen om een ​​vleugje originaliteit in hun ontwerp te introduceren.

Verschillende polygonen worden met dit doel gebruikt, zoals de bovenste valuta, de kroon genoemd en uit Tsjechië, een goed voorbeeld van het gebruik van Tridecágono als ontwerpelement.

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Tekening. Regelmatige polygonen. Hersteld van: tekenen.com.
3. Hartley, m. Een tridecagon construeren. Hersteld van: YouTube.com
4. Wikipedia. Bouwbare polygoon. Hersteld van: is.Wikipedia.borg.
5. Wikiwand. Tidecagon. Hersteld van: Wikiwand.com.