Escaleno trapezio -eigenschappen, formules en vergelijkingen, voorbeelden

A trapeze scaleen Het is een vierzijdige polygoon, waarvan er twee parallel aan elkaar zijn, en met zijn vier binnenhoeken van verschillende maatregelen.

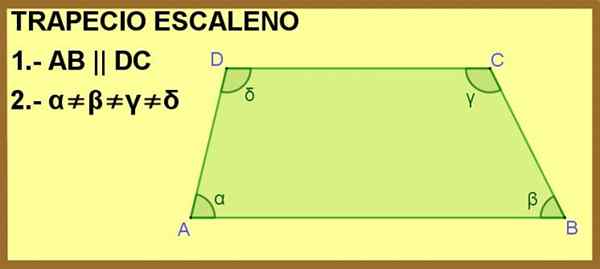
Het ABCD -vierhoek wordt getoond, waarbij de zijkanten AB en DC parallel aan elkaar zijn. Hiermee is het voldoende om er een trapeze van te maken, maar bovendien zijn de α-, β-, γ- en A -binnenhoeken allemaal verschillend, daarom is de trapezoid escalano.

Figuur 1. Het ABCD -vierhoek is een trapeze voor conditie 1 en scaleen voor toestand 2. Bron: f. Zapata.

[TOC]

Elementen van het Scaleno Trapect

Onder de meest karakteristieke elementen:

-Bases en zijde: De parallelle zijden van de trapezium zijn de bases en de twee niet -parallelle zijden zijn de zijkanten.

In een scalene trapezio zijn de bases van verschillende lengtes en ook de zijkanten. Een scaleen trapezoid kan echter een zijde van gelijke lengte hebben als basis.

-Mediaan: Het is het segment dat de middelpunten van de zijkanten verbindt.

-Diagonaal: De diagonaal van een trapeze is het segment dat zich bij twee tegenovergestelde hoekpunten verbindt. Een trapeze heeft, zoals elke vierhoek, twee diagonalen. In de scalene trapezio zijn ze van verschillende lengte.

Andere trapezoïden

Naast de Escaleno trapezio zijn er andere specifieke trapezoïden: de rechthoek trapezoid en de gelijkbenige trapezoid.

Een trapeze is rechthoek wanneer een van de hoeken recht is, terwijl Trapezio Isosceles zijn zijkanten van gelijke lengte heeft.

De trapeziumvormige vorm heeft talloze toepassingen op ontwerp- en industriële niveau, zoals in de configuratie van vliegtuigvleugels, de vorm van alledaagse objecten zoals tabellen, back -ups van stoelen, containers, portefeuilles, textielafdrukken en meer.

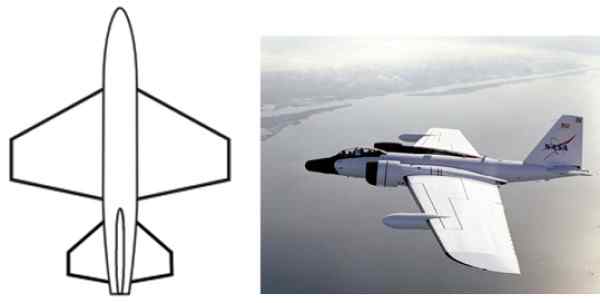Figuur 2. De trapeziumvormige vorm is gebruikelijk in de Alar -vliegtuigconfiguratie. Bron: Wikimedia Commons.

Eigenschappen

Vervolgens worden de eigenschappen van het klimtrapezoïde vermeld, waarvan vele uitgebreid zijn voor de andere soorten trapezoid. In wat volgt, wanneer u over "trapezio" praat, is het onroerend goed van toepassing op welke aard dan ook, inclusief de scalene.

1. De mediaan van de trapezium, dat wil zeggen het segment dat de middenpunten van zijn niet -parallelle zijden verenigt, is parallel aan een van de bases.

2.- De mediaan van een trapezium heeft een lengte die de semi -soum van zijn bases is en snijdt zijn diagonalen in het middelpunt.

3.- De diagonalen van een trapeze kruisen elkaar op een punt dat ze verdelen in twee secties die evenredig zijn met de verhouding van de bases.

4.- De som van de vierkanten van de diagonalen van een trapeze is gelijk aan de som van de vierkanten van zijn zijkanten plus het dubbele product van zijn bases.

5.- Het segment dat zich bij de middendiagonale punten verbindt, heeft lengte gelijk aan de semi -verwijzing van de bases.

Kan u van dienst zijn: injectieve functie: waar het uit bestaat, waarvoor is het en voorbeelden

6.- De hoeken grenzend aan de zijkanten zijn aanvullend.

7.- In een scaleen trapeze is de lengte van de diagonalen anders.

8.- Een trapeze heeft alleen een geregistreerde omtrek als de som van zijn bases gelijk is aan de som van zijn zijkanten.

9.- Als een trapeze een geregistreerde omtrek heeft, dan is de hoek met hoekpunt in het midden van genoemde omtrek en zijkanten die door de uiteinden van de laterale van de trapeze recht zijn.

10.- Een Escaleno Trapeze heeft geen omschreven omtrek, het enige type trapeze dat als het heeft het de gelijkbenige is.

Formules en vergelijkingen

De volgende relaties van de klimtrapeze worden verwezen naar de volgende figuur.

1.- Als AE = ED en BF = FC → EF || AB en EF || DC.

2.- Ef = (ab + dc)/2 dat is: m = (a + c)/2.

3.- Di = ib = D₁ /2 en Ag = GC = D₂ /2.

4.- Dj / jb = (c / a) Evenzo cj / ja = (c / a).

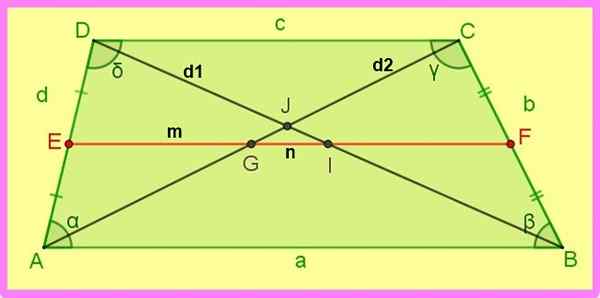figuur 3. Mediane en diagonalen van een scaleen trapezoid. Bron: f. Zapata.

5.- Db² + AC² = Advertentie² + BC² + 2 AB ∙ DC 

Gelijkwaardig:

D₁² + D₂² = D² + B² + 2 A ∙ C

6.- Gi = (ab - dc)/2

Het is te zeggen:

n = (a - c)/2

7.- α + Δ = 180⁰ en β + γ = 180⁰

8.- Als α ≠ β ≠ γ ≠ δ dan d1 ≠ d2.

9.- Figuur 4 toont een scaleen trapezoid dat een geregistreerde omtrek heeft, in dat geval is het vervuld dat:

A + C = D + B

10.- In een ABCD Escaleen Trapezoid met een geregistreerd centrum van het centrum of het volgende wordt ook vervuld:

∡aod = ∡boc = 90⁰

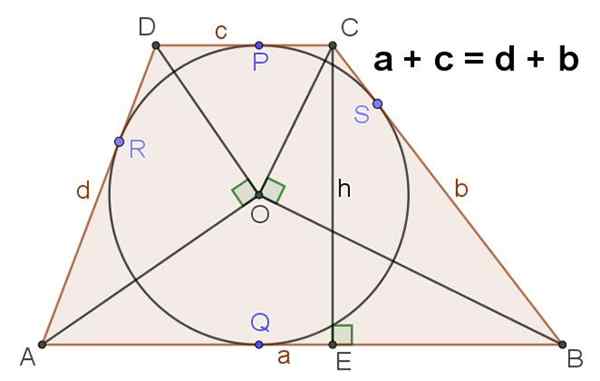Figuur 4. Als het in een trapeze wordt geverifieerd dat de som van zijn basen gelijk is aan de som van de zijkanten, dan is er de omtrek in hetzelfde ingeschreven. Bron: f. Zapata.

Hoogte

De hoogte van een trapeze wordt gedefinieerd als het segment dat van een punt van de basis loodrecht naar de tegenoverliggende basis (of de extensie) gaat.

Alle hoogten van de trapeze hebben dezelfde maat h, dus meestal verwijst het woordhoogte naar zijn meting. Kortom, hoogte is de afstand of scheiding tussen de bases.

De hoogte h kan worden bepaald als de lengte van een zijde en een van de hoeken grenzend aan de zijkant bekend is:

H = d sin (α) = d sin (γ) = b sin (β) = b sin (δ)

Mediaan

De M mediane maat van het trapezium is de semi -body's van de bases:

M = (a + b)/2

Diagonalen

D₁ = √ [a² + D² - 2 ∙ a ∙ d ∙ cos (α)]

D₂= √ [a² + B² - 2 ∙ a ∙ b ∙ cos (β)]

Het kan ook worden berekend als alleen de lengte van de trapezium bekend is:

D₁ = √ [B² + A ∙ c - a (b² - D²)/(a - c)]

D₂ = √ [D² + A ∙ C - A (D² - B²)/(a - c)]

Omtrek

De omtrek is de totale lengte van de contour, dat wil zeggen de som van al zijn zijden:

Kan u van dienst zijn: discrete willekeurige variabele

P = a + b + c + d

Gebied

Het gebied van een trapezoid is de semi -body's van zijn bases vermenigvuldigd met zijn hoogte:

A = H ∙ (A + B)/2

Het kan ook worden berekend als de mediane M en de hoogte bekend zijn:

A = M ∙ H

In het geval dat alleen de lengte van de trapeziumzijden bekend is, kan het gebied worden bepaald door de formule van Herón voor de trapezoid:

A = [(A+C)/| A-C |] ∙ √ [(S-A) (S-C) (S-A-D) (S-A-B)]]]

Waar s de semi -perimeter is: s = (a+b+c+d)/2.

Andere relaties voor de klimklim

De snede van de mediaan met de diagonalen en de parallel die door de kruising van de diagonalen gaat, geeft aanleiding tot andere relaties.

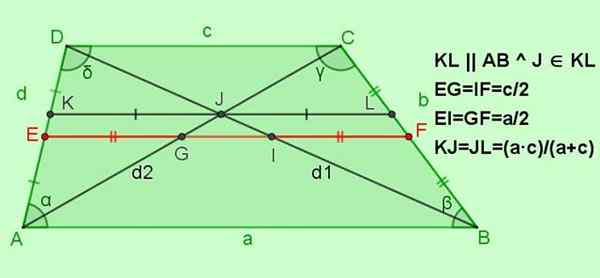Figuur 5. Andere relaties voor de klimklim. Bron: f. Zapata.

-Relaties voor mediane EF

Ef = (a+c)/2; Bijv. = If = c/2; Ei = gf = a/2

-Relaties voor het parallelle segment met de KL -basen, en dat gaat door het punt van Kruising J van de diagonalen

JA KL || AB || DC met J ∈ KL, dan kj = jl = (a ∙ c)/(a+c)

Constructie van het scaleen trapezium met heerschappij en kompas

Gegeven de basis van lengtes naar En C, een> c zijn en met kant van lengtes B en D, wezen B> D, We gaan verder met het volgen van deze stappen (zie figuur 6):

1.- Met de regel is het segment van de grootste AB getrokken.

2.- Van een SE en op AB is punt P gemarkeerd zodat AP = C.

3.- Met het kompas met C en Radio D Center is een boog getrokken.

4.- Het wordt in B. in B gemaakt met radio B die een boog tekent die de boog interpreteert die in de vorige stap is opgesteld. We noemen dat het snijpunt.

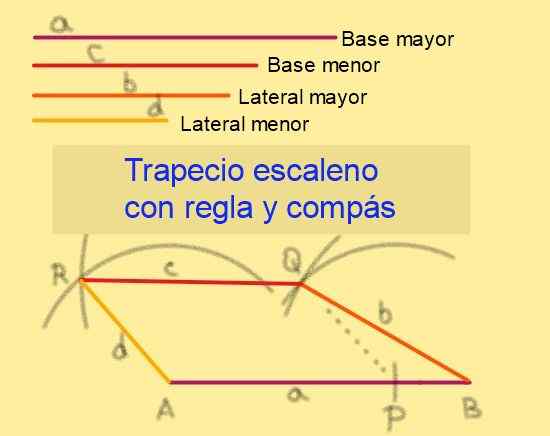Figuur 6. Constructie van Escaleno Trapecio gegeven zijn partijen. Bron: f. Zapata.

5.- Met centrum bij het tekenen van een straalboog d.

6.- Met centrum om een ​​straalboog te tekenen die onderschepte naar de boog opgesteld in de vorige stap. Het zal R tot het snijpunt worden genoemd.

7.- De segmenten BQ, QR en RA worden getekend met de regel.

8.- De ABQR -vierhoek is een scaleen trapezoïde, omdat APQR een parallellogram is, dat garandeert dat ab || QR.

Voorbeeld

De volgende lengtes worden gegeven in CM: 7, 3, 4 en 6.

a) Bepaal of u met hen een scaleen -trapeze kunt bouwen die kan omschrijven naar een omtrek.

b) Vind de perimeter, het gebied, de lengte van de diagonalen en de hoogte van genoemde trapeze, evenals de straal van de geregistreerde omtrek.

- Oplossing voor

Met behulp van de segmenten van lengte 7 en 3 als basen en die van lengte 4 en 6 als zijkanten, kan een scaleen trapezoid worden gebouwd met behulp van de procedure beschreven in de vorige sectie.

We moeten controleren of het een geregistreerde omtrek heeft, maar het onthouden van het onroerend goed (9):

Kan je van dienst zijn: zeshoekige prisma

Een trapeze heeft alleen een geregistreerde omtrek als de som van zijn bases gelijk is aan de som van zijn zijkanten.

We zien dat inderdaad:

7 + 3 = 4 + 6 = 10

Vervolgens wordt voldaan aan de toestand van de ingeschreven omtrek.

- Oplossing B

Omtrek

Perimeter P wordt verkregen door de zijkanten toe te voegen. Aangezien de bases in totaal 10 en de zijkanten ook, is de perimeter:

P = 20 cm

Gebied

Om het gebied te bepalen, wordt alleen de kanten bekendgemaakt, de relatie wordt toegepast:

A = [(A+C)/| A-C |] ∙ √ [(S-A) (S-C) (S-A-D) (S-A-B)]]]

Waar s de semi -perimeter is:

S = (A+B+C+D)/2.

In ons geval is de semi -perimeter s = 10 cm waard. Na het vervangen van de respectieve waarden:

A = 7 cm; B = 6 cm; C = 3 cm; D = 4 cm

Is overgebleven:

A = [10/4] √ [(3) (7) (-1) (-3)] = (5/2) √63 = 19,84 cm².

Hoogte

Hoogte H is gerelateerd aan gebied A tot en met de volgende uitdrukking:

A = (a+c) ∙ h/2, waarbij de hoogte kan worden verkregen door klaring:

H = 2a / (a+c) = 2 * 19.84 / 10 = 3.968 cm.

Geregistreerde omtrekradio

De straal van de geregistreerde omtrek is de helft van de hoogte waard:

R = h/2 = 1.984 cm

Diagonalen

Eindelijk is er de lengte van de diagonalen:

D₁ = √ [B² + A ∙ c - a (b² - D²)/(a - c)]

D₂ = √ [D² + A ∙ C - A (D² - B²)/(a - c)]

De waarden correct vervangen zijn:

D₁ = √ [6² + 7 ∙ 3 - 7 (6² - 4²)/(7 - 3)] = √ (36+21-7 (20)/4) = √ (22)

D₂ = √ [4² + 7 ∙ 3 - 7 (4² - 6²)/(7-3)] = √ (16+21-7 (-20)/4) = √ (72)

Dat is: D₁ = 4,69 cm en D₂ = 8,49 cm

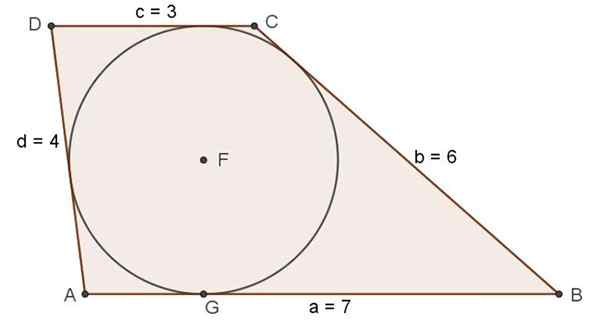Figuur 7. Scalene trapezio die voldoet aan de staat van het bestaan ​​van geregistreerde omtrek. Bron: f. Zapata.

Oefening opgelost

Bepaal de interieurhoeken van de basis trapezoid AB = a = 7, CD = C = 3 en lateraal BC = B = 6, da = d = 4.

Oplossing

De cosinus -stelling kan worden toegepast om de hoeken te bepalen. De hoek ∠a = α wordt bijvoorbeeld bepaald uit de driehoek ABD met ab = a = 7, bd = d2 = 8,49 en da = d = 4.

De cosinus -stelling die op deze driehoek wordt toegepast, blijft zo:

D₂² = a² + D² - 2 ∙ a ∙ d ∙ cos (α), dat wil zeggen:

72 = 49+16-56 ∙ cos (α).

Bij het opruimen wordt de cosinus van de hoek α verkregen:

Cos (α) = -1/8

Dat wil zeggen dat α = arccos (-1/8) = 97.18⁰.

Op dezelfde manier worden de andere hoeken verkregen, hun waarden zijn:

β = 41.41⁰; γ = 138,59⁰ en uiteindelijk Δ = 82,82⁰.

Referenties

1. C. EN. NAAR. (2003). Geometrie -elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Wiskunde 2. Patria -redactiegroep.
3. Vrijgelaten, k. (2007). Ontdek polygonen. Benchmark -onderwijsbedrijf.
4. Hendrik, V. (2013). Gegeneraliseerde polygonen. Birkhäuser.
5. Iger. (S.F.)). Wiskunde eerste semester Tacaná. Iger.
6. Jr. Geometrie. (2014). Polygonen. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Wiskunde: redeneren en applicaties (tiende editie). Pearson Education.
8. Patiño, m. (2006). Wiskunde 5. Redactionele progreso.
9. Wikipedia. Trapeze. Hersteld van: is.Wikipedia.com